学习顺序：

1. 学会使用STL的基本用法
2. 学会使用STL解决问题
3. 学会用一维数组模拟栈，解决问题

栈是只能在某一端插入和删除的特殊线性表

stack stk

stack<int> s;
s.push(3);
s.push(2);
s.push(5);
cout << s.top(); // 5
s.pop();
cout << s.top(); // 2

一维数组模拟栈

https://www.acwing.com/problem/content/830/

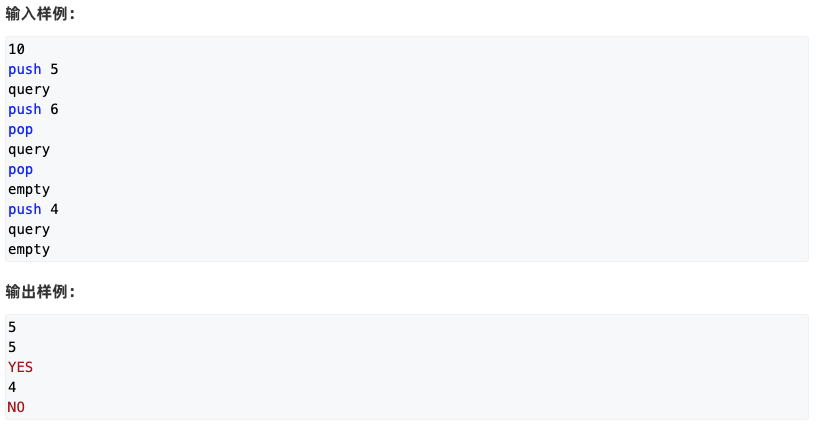
// tt指针初始化为0，第一个数存在1上，当tt==0的时候，代表空栈
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int stk[N];
int tt = 0;
int main()
{
    int M;
    cin >> M;
    string op;
    int x;
    while (M--)
    {
        cin >> op;
        if (op == "push")
        {
            cin >> x;
            stk[++tt] = x;
        }
        if (op == "pop")
        {
            tt--;
        }
        if (op == "empty")
        {
            if (tt == 0) cout << "YES" << endl;
            else cout << "NO" << endl;
        }
        if (op == "query")
        {
            cout << stk[tt] << endl;
        }
    }
    return 0;
}

例题，【例1-2】后缀表达式的值

//用一个栈维护数字，用一个栈维护运算符
//这道题目没有括号，另外注意运算数的数值范围比较大
//不开LL见祖宗

例题，表达式括号匹配(stack)

//用一个栈维护左括号和右括号的关系
//右括号，没有左括号配对就是非法
//左括号，最后没有右括号配对就是非法

例题，车厢调度(train)

//第一种方法，把一系列车厢，当成一个数组，1, 2, 3, 4, ..., n
//x读进来了，那么，我们就要认为：x之后的数字，都不应该出现在栈中；x之前的数字没入栈的都应该入栈
//标记在不在栈里的方法，1代表在栈里面，2代表已经出栈
//第二种方法，用一个stack硬来模拟这个进出栈的过程(冷不丁让我重写，我想我是模拟不出来的)
//如果stack空的，把前面没入栈的入栈
//如果stack非空，栈顶元素如果比我大，那是非法的；
//整个过程中，用一个变量tp，初始值设为1，来维护栈顶元素的值

例题，中缀表达式值(expr)

//在这道题目上，我一共花费了4个小时
//所以，我建议你自己做，研究至少花费2个小时。
//可以很好的提升代码能力，加深对栈的理解，对表达式的理解
//第一种方法，直接利用中缀表达式，进行求解，这个方法和前面的题目类似
//第二种方法，中缀读进来，然后转成后缀
//后缀的建立，用一个queue<node>进行维护，node可以是运算数，也可以是运算符
//node需要使用struct定义一下
//关于非法情况的判断
//首先这道题目的数据，没有那么严格，不需要判断除数不能为0的情况
//其他非法，左右括号不匹配问题；只有一位，这一位还是运算符; 上来第一位是+*/运算符，负号是可以的
//中缀表达式，两个运算符连在一块了；右括号没有左括号匹配，左括号没有右括号匹配
//网上能搜到题解，对左括号个数和右括号个数相同作为配对的原则，这个其实不严谨
//运算符优先级，可以写一个函数实现，也可以写一个map预设好

例题，P1981 [NOIP2013 普及组] 表达式求值

#include <iostream>
#include <cstring>
#include <algorithm>
#include <stack>
#include <unordered_map>
using namespace std;
const int MOD = 10000;
stack<int> num;
stack<char> op;
void eval()
{
    int b = num.top(); num.pop();
    int a = num.top(); num.pop();
    char c = op.top(); op.pop();
    if (c == '+') num.push((a + b) % MOD);
    else num.push(a * b % MOD);
}
int main()
{
    string s;
    cin >> s;
    unordered_map<char, int> pr{{'+', 1}, {'*', 2}};
    for (int i = 0; i < s.size(); i ++ )
    {
        if (isdigit(s[i]))
        {
            int j = i, x = 0;
            while (j < s.size() && isdigit(s[j])) x = x * 10 + s[j ++ ] - '0';
            num.push(x % MOD);
            i = j - 1;
        }
        else
        {
            while (op.size() && pr[op.top()] >= pr[s[i]]) eval();
            op.push(s[i]);
        }
    }
    while (op.size()) eval();
    cout << num.top() << endl;
    return 0;
}
// 以后的习题中，会涉及一个表示式树的题目