dp动态规划(三)背包九讲

背包问题是线性DP中一类重要而特殊的模型。前面，我们已经初步的领略了01背包问题。

接下来，我们扩展一下，并且认识模板。

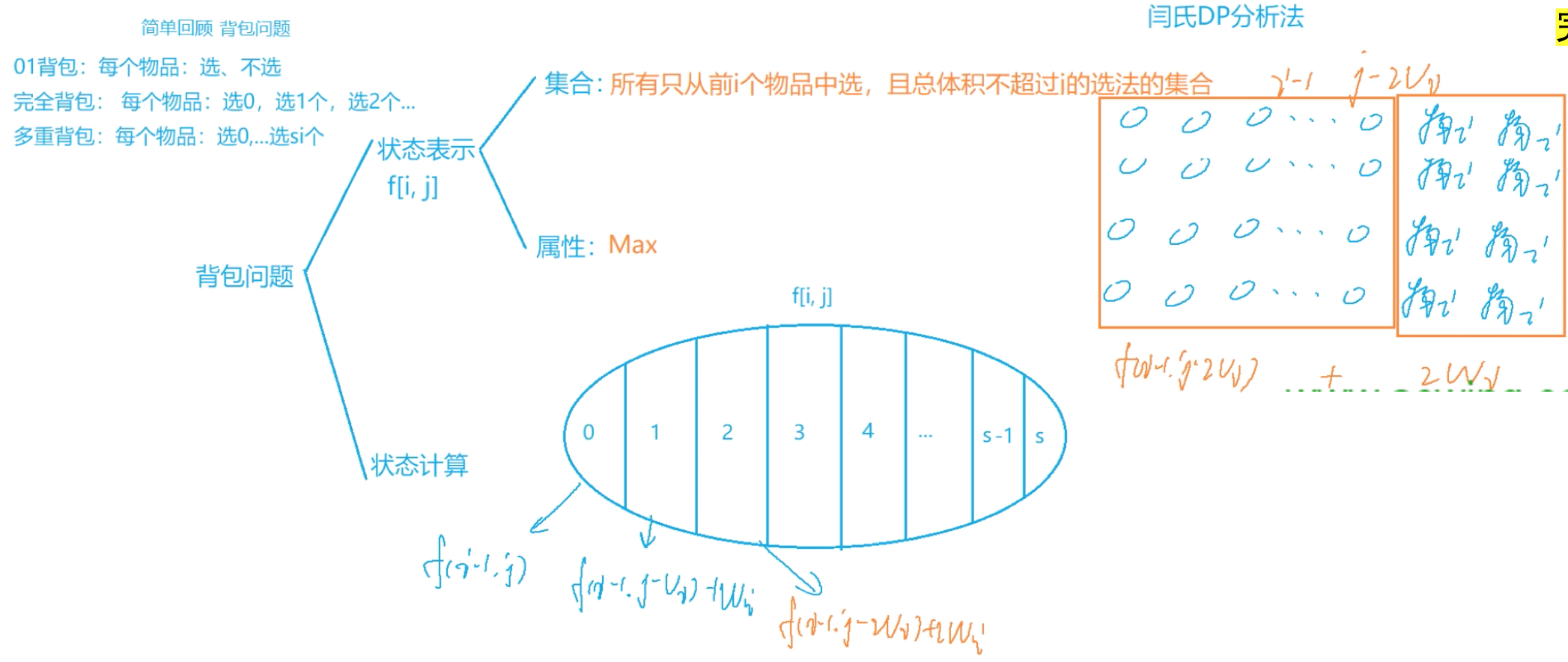
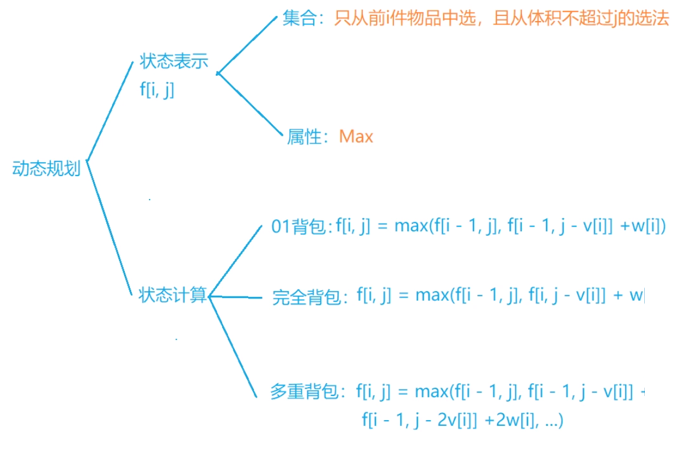
0/1背包问题

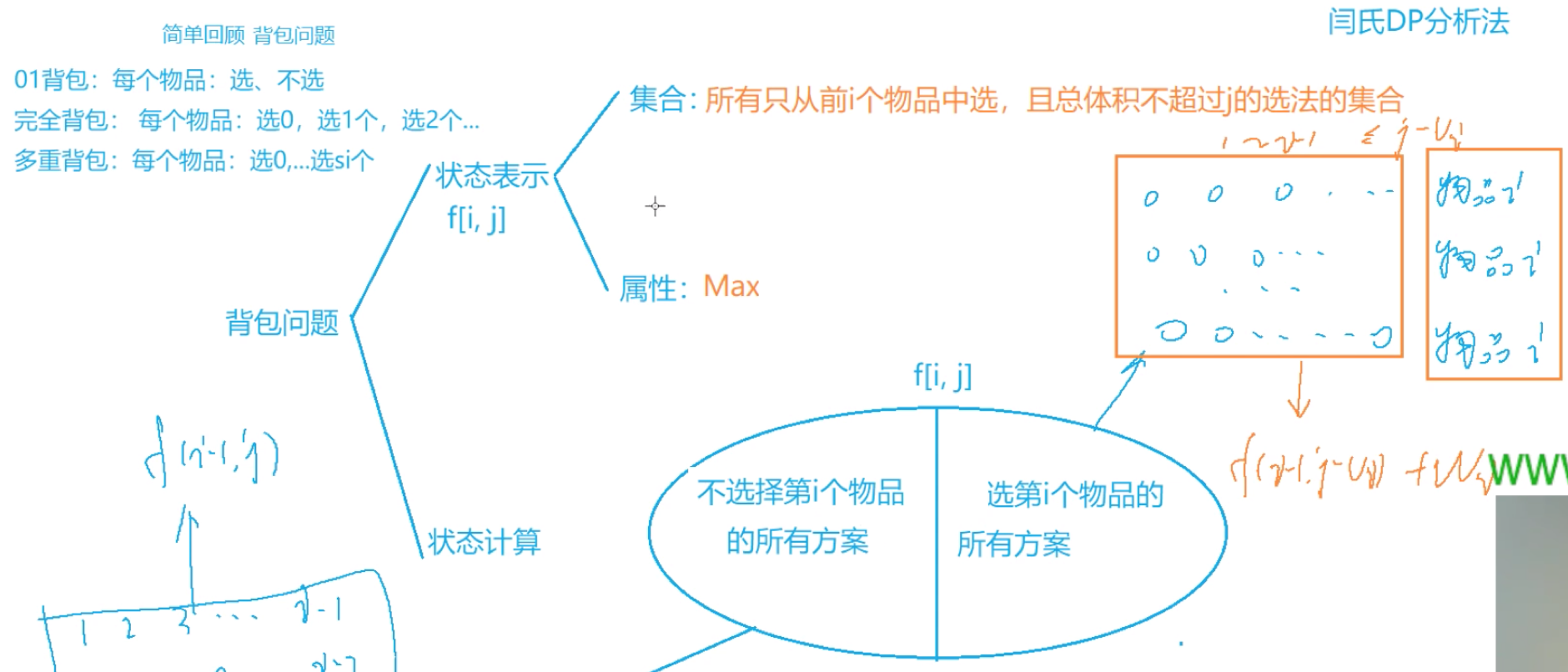
例题：01背包问题

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];
    for (int i = 1; i <= n; i++)
        for (int j = 0; j <= m; j++)
        {
            f[i][j] = f[i - 1][j];  // 右边集合为空，不包含i
            if (j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
        }
    cout << f[n][m] << endl;
    return 0;
}

// 滚动数组优化，f[N][M] -> f[2][M]
#include <iostream>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[2][N];   
//计算f[i]这一层，只用到了f[i-1]这一层的数据，用滚动数组
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];
    f[0][0] = 0;
    for (int i= 1; i <= n; i++)
        for (int j = 0; j <= m; j++)
        {
            f[i & 1][j] = f[(i - 1) & 1][j];
            if (j >= v[i]) f[i & 1][j] = max(f[i & 1][j], f[(i - 1) & 1][j - v[i]] + w[i]);
        }
    cout << f[n & 1][m] << endl;
    return 0;
}

// 二维优化到一维
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];   
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];
    for (int i = 1; i <= n; i++)
        for (int j = m; j >= v[i]; j--)
        {
            f[j] = max(f[j], f[j - v[i]] + w[i]);
            //这与我们的刚才的二维里的状态计算不一致，刚才实际应该是f[i - 1][j - v[i]]
            //若j从大到小枚举，算f[j]的时候，f[j - v[i]]还没有被更新过，存的就是f[i - 1][j - v[i]]
            //这样就和二维的状态转移方程等价了
        }
    cout << f[m] << endl;
    return 0;
}

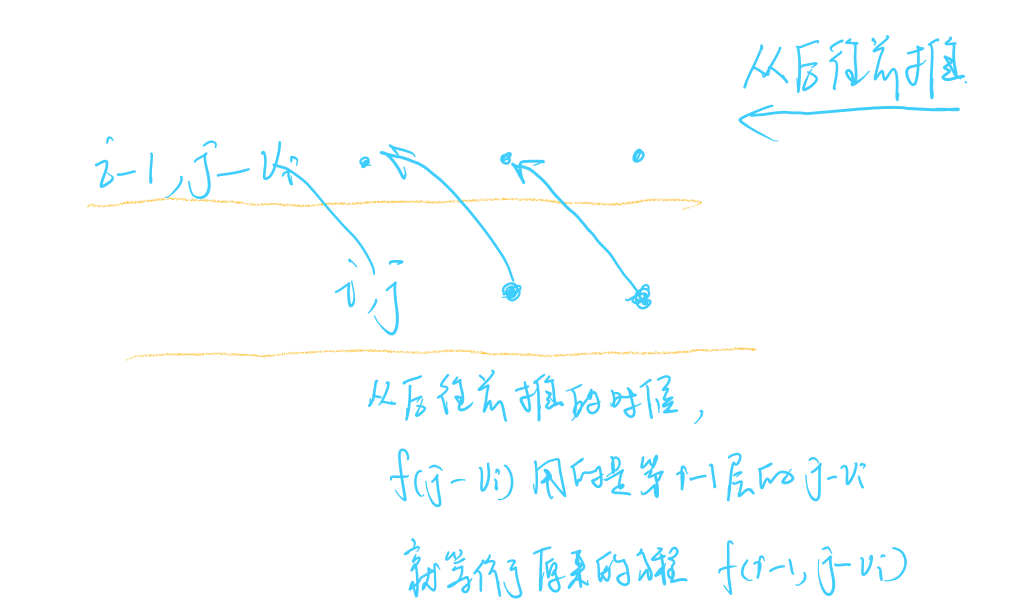
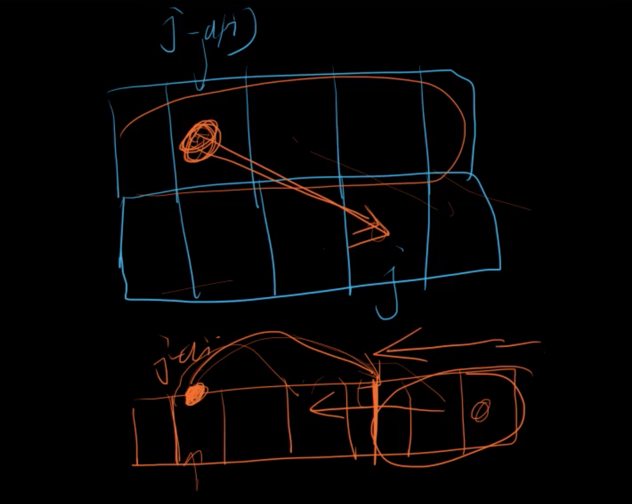
// define ZerOnePack
#include <iostream>
using namespace std;
const int N = 1010;
int n, m;
int f[N];
int v[N], w[N];
void zeroonepack(int f[N], int vi, int wi)
{
    for (int j = m; j >= vi; j--)
        f[j] = max(f[j], f[j - vi] + wi);
}
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];
    for (int i = 1; i <= n; i++)
        zeroonepack(f, v[i], w[i]);
    cout << f[m] << endl;
    return 0;
}

初始化的细节问题

完全背包问题

例题：完全背包问题

// 3 loops
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];
    /*
    for 物品
        for 体积
            for 决策
    */
    for (int i = 1; i <= n; i++)
        for (int j = 0; j <= m; j++)
            for (int k = 0; k *v[i] <= j; k++)
                f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);
    cout << f[n][m] << endl;
    return 0;
}

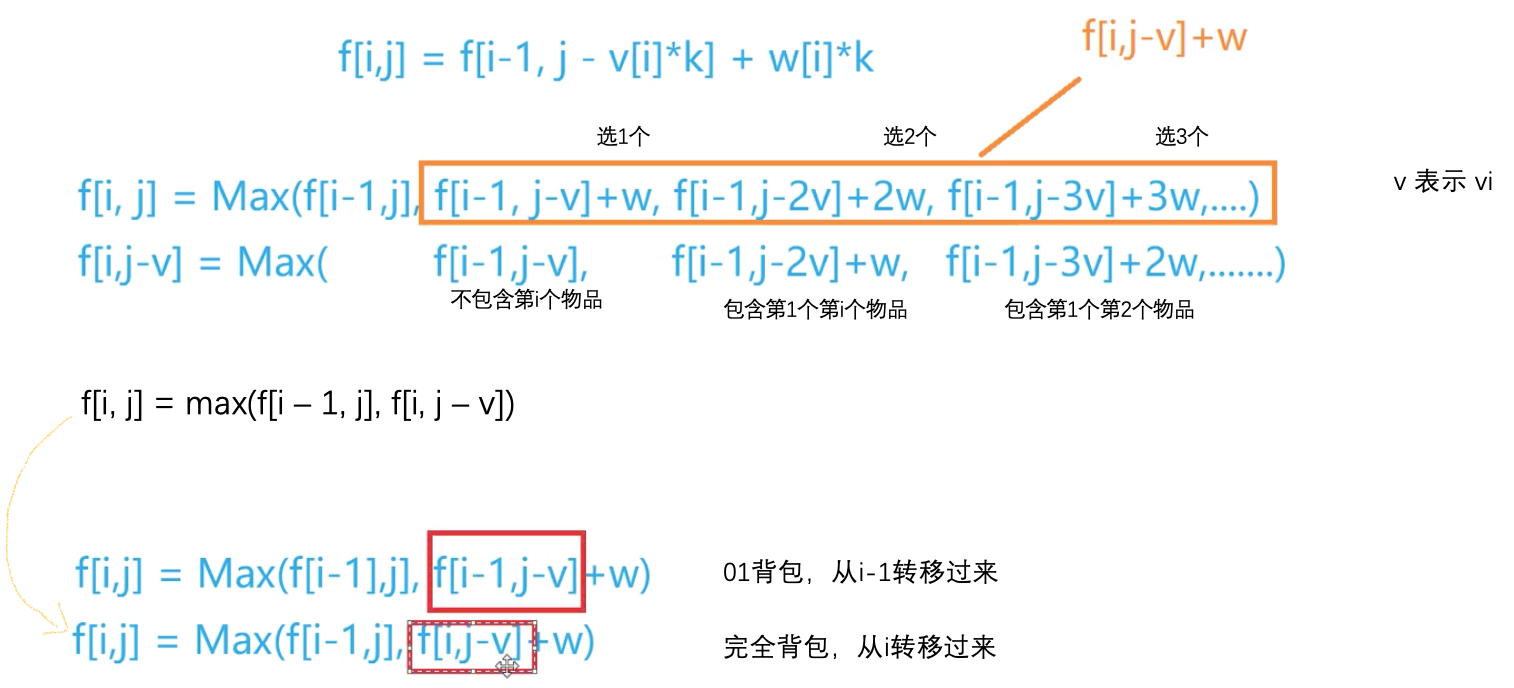
// 根据以上对转移方程的数学分析
// 3 loops -> 2 loops，减少了一层k循环
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];
    for (int i = 1; i <= n; i++)
        for (int j = 0; j <= m; j++)
        {
            f[i][j] = f[i - 1][j];
            if (j >= v[i]) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
        }
    cout << f[n][m] << endl;
    return 0;
}

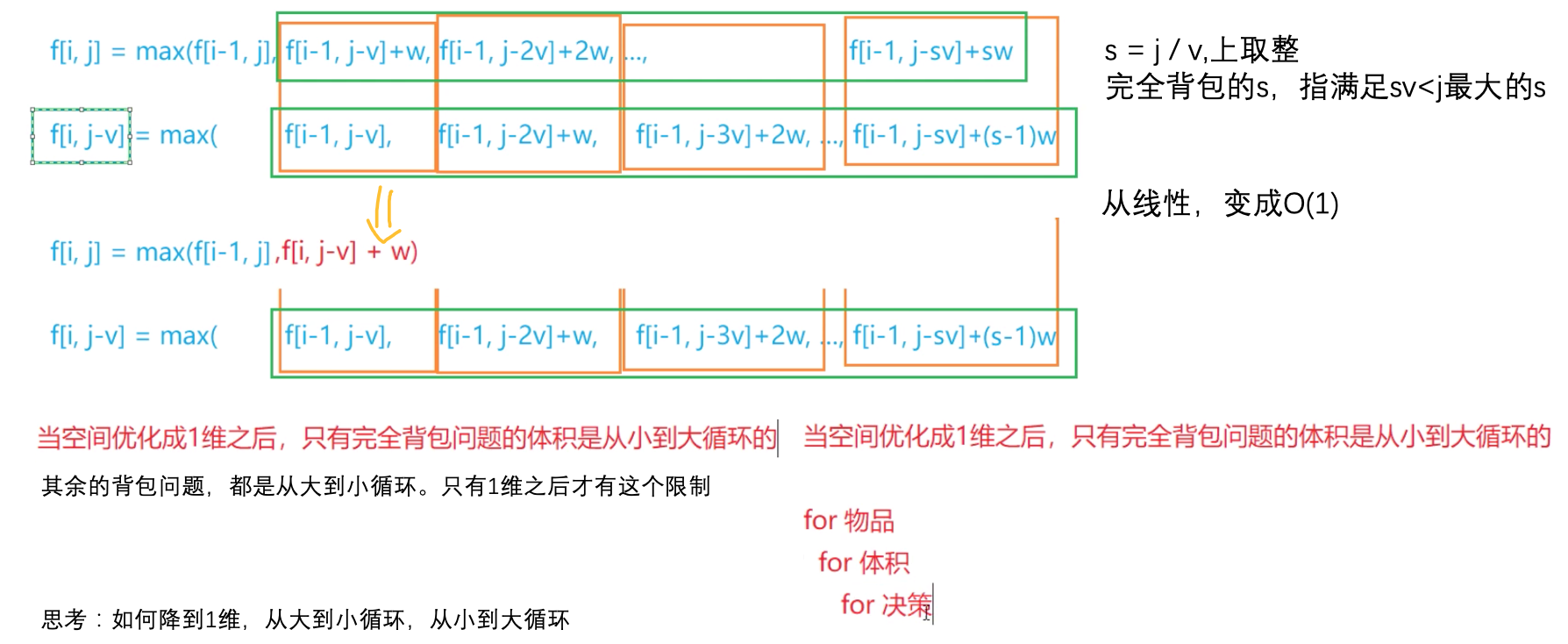
二维变成一维 求f[j]的时候，f[j–v[i]]已经被算过了， f[j-vi]是第i层的 f[j-vi] 和状态转移方程一致

// f[i][j] -> f[j]
// 二维变一维
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];
    for (int i = 1; i <= n; i++)
        for (int j = v[i]; j <= m; j++)
            f[j] = max(f[j], f[j - v[i]] + w[i]);
    cout << f[m] << endl;
    return 0;
}

想清楚： 一维的写法，为什么只差了从大到小循环 和 从小大到循环

// define completepack
#include <iostream>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];
void completepack(int f[], int vi, int wi)
{
    for (int j = vi; j <= m; j++)
        f[j] = max(f[j], f[j - vi] + wi);
}
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];
    for (int i = 1; i <= n; i++)
        completepack(f, v[i], w[i]);
    cout << f[m] << endl;
    return 0;
}

多重背包问题

例题：多重背包问题 I

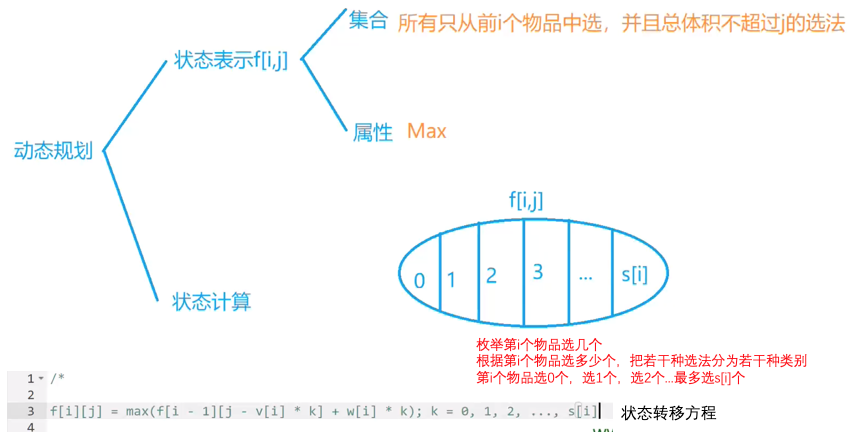
// 多重背包问题 I
// 0 < N,V ≤ 100
// 0 < vi,wi,si ≤ 100
// 3 loops
// O(n^3)
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
int n, m;
int v[N], w[N], s[N];
int f[N][N];
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i] >> s[i];
    for (int i = 1; i <= n; i++)
        for (int j = 0; j <= m; j++)
            for (int k = 0; k <= s[i] && k * v[i] <= j; k++)
                f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);
    cout << f[n][m] << endl;
    return 0;
}

例题：多重背包问题 II，倍增

// 多重背包问题 II
// 0 < N ≤ 1000
// 0 < V ≤ 2000
// 0 < vi,wi,si ≤ 2000
// 3loops 会TLE，这里用到二进制优化（倍增思想），转化成01背包问题

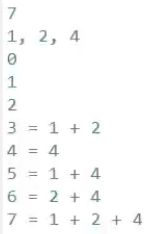一个数，可以用几个表示出来
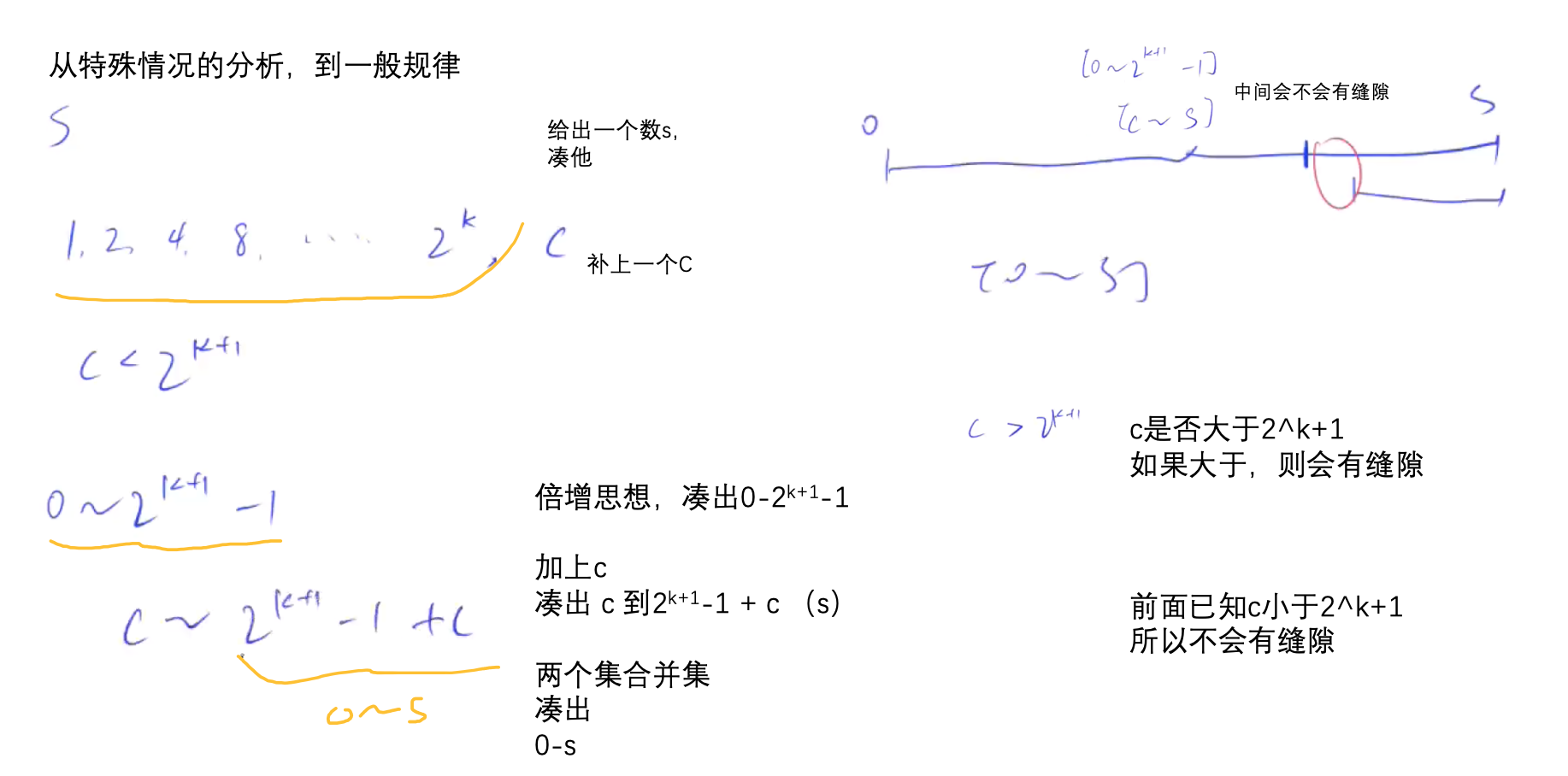
不是一个数，恰好可以用几个表示出来，还会有一点余份，比如10，用124可以表示0-7，多来一个3，就可以表示0-10。（不能用1248来表示，因为就会表示多了，11-15也可以表示了）

// 多重背包问题 II
// O(NVlogs)
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 25000, M = 2010;
int n, m;
int v[N], w[N];
int f[N];
int main()
{
    cin >> n >> m;
    int cnt = 0;
    for (int i = 1; i <= n; i++)
    {
        int a, b, s;
        cin >> a >> b >> s;
        int k = 1;
        while (k <= s)
        {
            cnt++;
            v[cnt] = a * k;
            w[cnt] = b * k;
            s -= k;
            k *= 2;
        }
        if (s > 0)
        {
            cnt++;
            v[cnt] = a * s;
            w[cnt] = b * s;
        }
    }
    n = cnt;
    for (int i = 1; i <= n; i++)
        for (int j = m; j >= v[i]; j--)
            f[j] = max(f[j], f[j - v[i]] + w[i]);
    cout << f[m] << endl;
    return 0;
}

// define multiplepack
#include <iostream>
using namespace std;
const int N = 1010, M = 2010;
int n, m;
int v[N], w[N], s[N];
int f[M];
void zeroonepack(int f[], int vi, int wi)
{
    for (int j = m; j >= vi; j--)
        f[j] = max(f[j], f[j - vi] + wi);
}
void completepack(int f[], int vi, int wi)
{
    for (int j = vi; j <= m; j++)
        f[j] = max(f[j], f[j - vi] + wi);
}
void multiplepack(int f[], int vi, int wi, int si)
{
    if (vi * si >= m){
        completepack(f, vi, wi);
        return ;
    }
    int k = 1;
    while (k < si){
        zeroonepack(f, k*vi, k*wi);
        si -= k;
        k *= 2;
    }
    if (si){
        zeroonepack(f, si*vi, si*wi);
    }
}
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++){
        cin >> v[i] >> w[i] >> s[i];
        multiplepack(f, v[i], w[i], s[i]);
    }
    cout << f[m] << endl;
    return 0;
}

例题：多重背包问题 III，单调队列优化

// 多重背包问题 III
// 0<N≤1000
// 0<V≤20000
// 0<vi,wi,si≤20000
// O(NVlogs)也会爆缸
// 需要使用单调队列优化方法

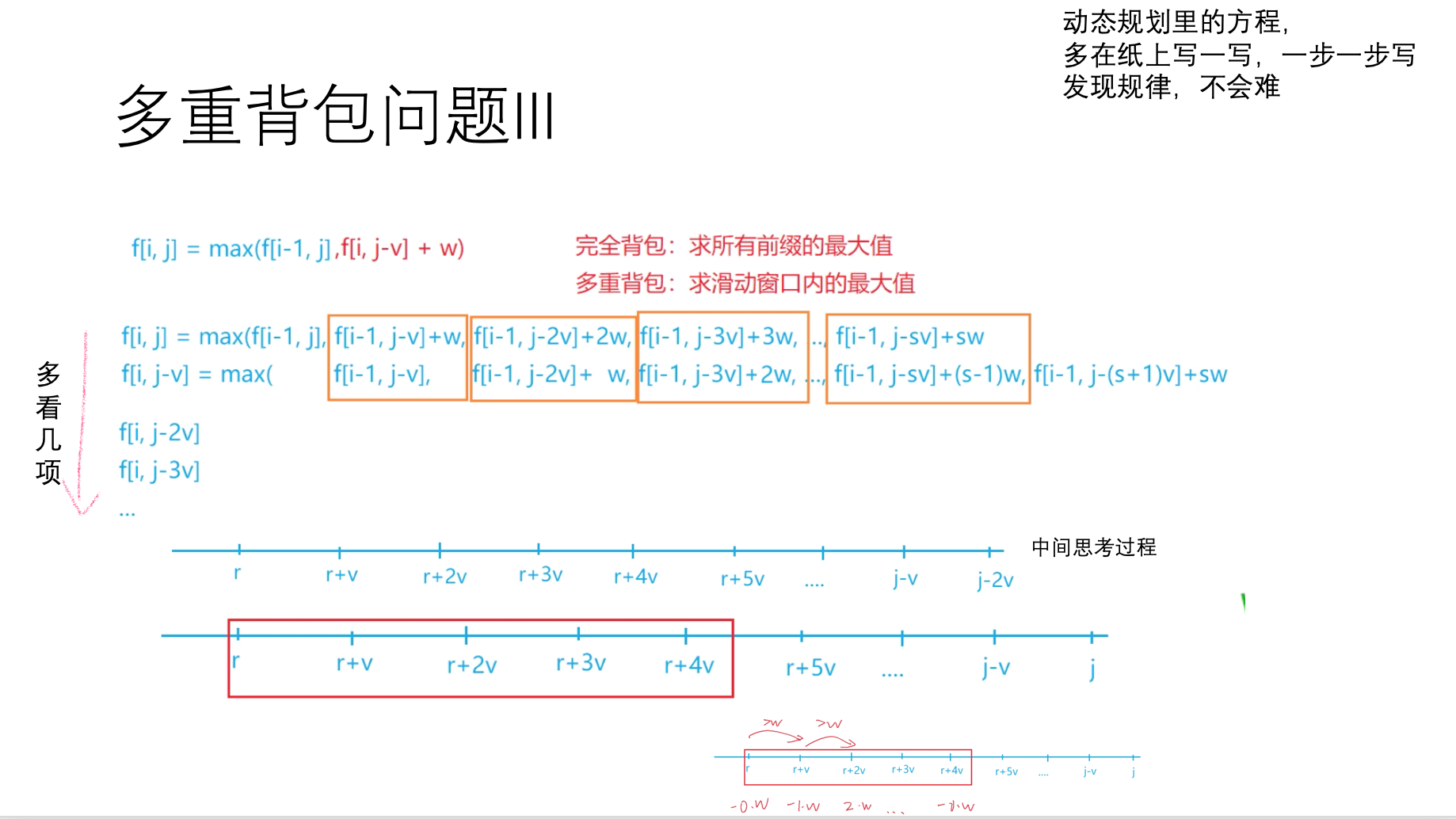
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 20010;
int n, m;
int f[N], g[N], q[N];
int main()
{
    cin >> n >> m;
    for (int i = 0; i < n; i++)
    {
        int v, w, s;
        cin >> v >> w >> s;
        memcpy(g, f, sizeof f);
        for (int j = 0; j < v; j++)
        {
            int hh = 0, tt = -1;
            for (int k = j; k <= m; k += v)
            {
                if (hh <= tt && q[hh] < k- s * v) hh++;
                if (hh <= tt) f[k] = max(f[k], g[q[hh]] + (k - q[hh]) / v * w);
                while (hh <= tt && g[q[tt]] - (q[tt] - j) / v * w <= g[k] - (k - j) / v * w)  tt--;
                q[++tt] = k;
            }
        }
    }
    cout << f[m] << endl;
    return 0;
}

混合三种背包问题

01背包

def ZeroOnePack(F, C, W ) 
    for v = V to C
        F[v] = max(F[v],f[v − C] + W)
for i = 1 to N 
    ZeroOnePack(F, Ci, Wi)

完全背包

def CompletePack(F, C, W ) 
    for v = C to V
        F[v] = max{F[v],f[v − C] + W}

多重背包

def MultiplePack(F, C, W, M) 
    if C·M ≥ V
        CompletePack(F, C, W)
        return
    k := 1
    while k < M
        ZeroOnePack(kC, kW) M := M − k
        k := 2k
    ZeroOnePack(C·M, W·M)

01背包+完全背包的混合

for i = 1 to N
    if 第i件物品属于01背包
        for v = V to Ci
            F[v] = max(F[v],F[v − Ci] + Wi)
    else if 第i件物品属于完全背包
        for v = Ci to V
            F[v] = max(F[v],F[v − Ci] + Wi)

01背包+完全背包+多重背包的混合

for i = 1 to N
    if 第i件物品属于01背包
        ZeroOnePack(F ,Ci ,Wi ) 
    else if 第i件物品属于完全背包
        CompletePack(F ,Ci ,Wi )
    else if 第i件物品属于多重背包 
        MultiplePack(F ,Ci ,Wi ,Ni )

例题：混合背包问题

#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int f[N];
int main()
{
    cin >> n >> m;
    for (int i = 0; i < n; i++)
    {
        int v, w, s;
        cin >> v >> w >> s;
        if (s == 0) //完全背包
        {
            for (int j = v; j <= m; j++) f[j] = max(f[j], f[j - v] + w);
        }
        else
        {
            if (s == -1) s = 1;
            for (int k = 1; k <= s; k *= 2)
            {
                for (int j = m; j >= k * v; j--)
                    f[j] = max(f[j], f[j - k * v] + k * w);
                s -= k;    
            }
            if (s)
            {
                for (int j = m; j >= s * v; j--)
                    f[j] = max(f[j], f[j - s * v] + s * w);
            }
        }
    }
    cout << f[m] << endl;
    return 0;
}
// 也可以存起来，再来一遍
#include <bits/stdc++.h>
using namespace std;
const int N = 40, M = 220, MM = 1e5 + 10;
int dp[N][M], w[N], v[N], s[N];
int V, n;
int f[MM], nw[MM], nv[MM], tot, knap[MM];
int main()
{
    cin >> V >> n;
    for (int i = 1; i <= n; i++){
        cin >> w[i] >> v[i] >> s[i];
        if (s[i] == 0){
            nw[++tot] = w[i]; nv[tot] = v[i];
            knap[tot] = 1;    //完全背包
        }
        else if (s[i] == 1){   //01背包
            nw[++tot] = w[i]; nv[tot] = v[i];
        }
        else{    //多重背包
            for (int j = 1; j <= s[i]; j = j << 1){
                s[i] -= j;
                nw[++tot] = w[i] * j; nv[tot] = v[i] * j;
            }
            if (s[i]){
                nw[++tot] = w[i] * s[i]; nv[tot] = v[i] * s[i];
                s[i] = 0;
            }
        }
    }
    for (int i = 1; i <= tot; i++){
        if (knap[i]){
            for (int j = nw[i]; j <= V; j++)
                f[j] = max(f[j], f[j - nw[i]] + nv[i]);
        }
        else{
            for (int j = V; j >= nw[i]; j--)
                f[j] = max(f[j], f[j - nw[i]] + nv[i]);
        }
    }
    cout << f[V] << '\n';
    return 0;
}

// define func()
#include <iostream>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N], s[N];
int f[N];
void zeroonepack(int f[], int vi, int wi)
{
    for (int j = m; j >= vi; j--)
        f[j] = max(f[j], f[j - vi] + wi);
}
void completepack(int f[], int vi, int wi)
{
    for (int j = vi; j <= m; j++)
        f[j] = max(f[j], f[j - vi] + wi);
}
void multiplepack(int f[], int vi, int wi, int si)
{
    if (vi * si >= m){
        completepack(f, vi, wi);
        return ;
    }
    int k = 1;
    while (k < si){
        zeroonepack(f, k*vi, k*wi);
        si -= k;
        k *= 2;
    }
    if (si){
        zeroonepack(f, si*vi, si*wi);
    }
}
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++){
        cin >> v[i] >> w[i] >> s[i];
        if (s[i] == -1) zeroonepack(f, v[i], w[i]);
        else if (s[i] == 0) completepack(f, v[i], w[i]);
        else multiplepack(f, v[i], w[i], s[i]);
    }
    cout << f[m] << endl;
    return 0;
}

二维费用背包

例题：二维费用的背包问题

#include <iostream>
using namespace std;
const int N = 110;
int n, V, M;
int f[N][N];
int main()
{
    cin >> n >> V >> M;
    for (int i = 0; i < n; i++)
    {
        int v, m, w;
        cin >> v >> m >> w;
        for (int j = V; j >= v; j--)
            for (int k = M; k >= m; k--)
                f[j][k] = max(f[j][k], f[j - v][k - m] + w);
    }
    cout << f[V][M] << endl;
    return 0;
}

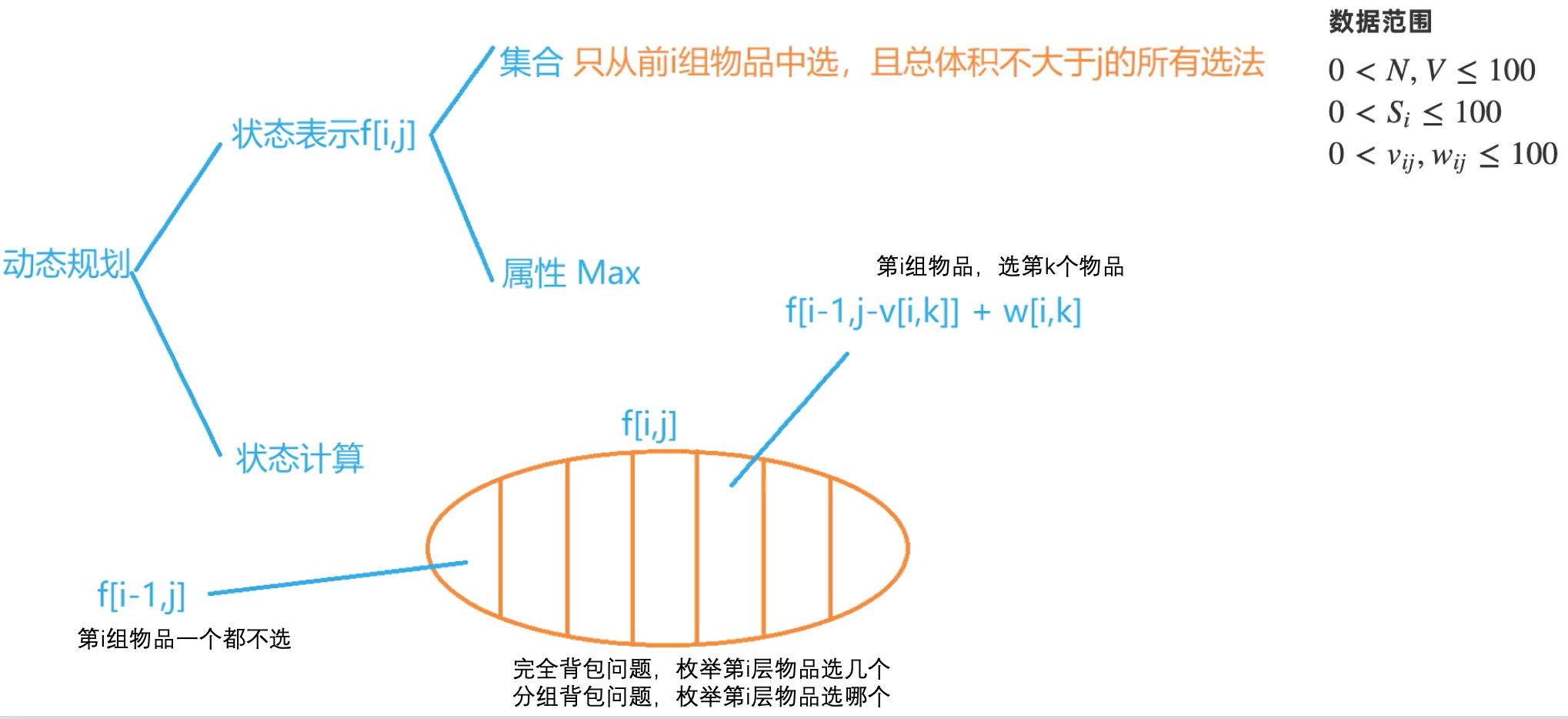
分组背包

例题：分组背包问题

// 这个问题变成了每组物品有若干种策略:是选择本组的某一件，还是一件 都不选
// 这里三层循环的顺序保证了每一组内的物品最多只有一个会被添加到背包中
// 分组的背包问题将彼此互斥的若干物品称为一个组，这建立了一个很好的模型
// 不少背包问题的变形都可以转化为分组的背包问题
// 由分组的背包问题进一步可定义“泛化物品”的概念，十分有利于解题
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
int n, m;
int v[N][N], w[N][N], s[N];
int f[N];
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
    {
        cin >> s[i];
        for (int j = 0; j < s[i]; j++)
            cin >> v[i][j] >> w[i][j];
    }
    for (int i = 1; i <= n; i++)
        for (int j = m; j >= 0; j--)
            for (int k = 0; k < s[i]; k++)
                if (v[i][k] <= j)
                    f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
    cout << f[m] << endl;
    return 0;    
}

例题：1272：【例9.16】分组背包

    for (int i = 1; i <= T; i++)
        for (int j = v; j >= 0; j--)
            for (int k = 0; k < (int)h[i].size(); k++)
                if (j >= h[i][k].first)
                    dp[j] = max(dp[j], dp[j - h[i][k].first] + h[i][k].second);

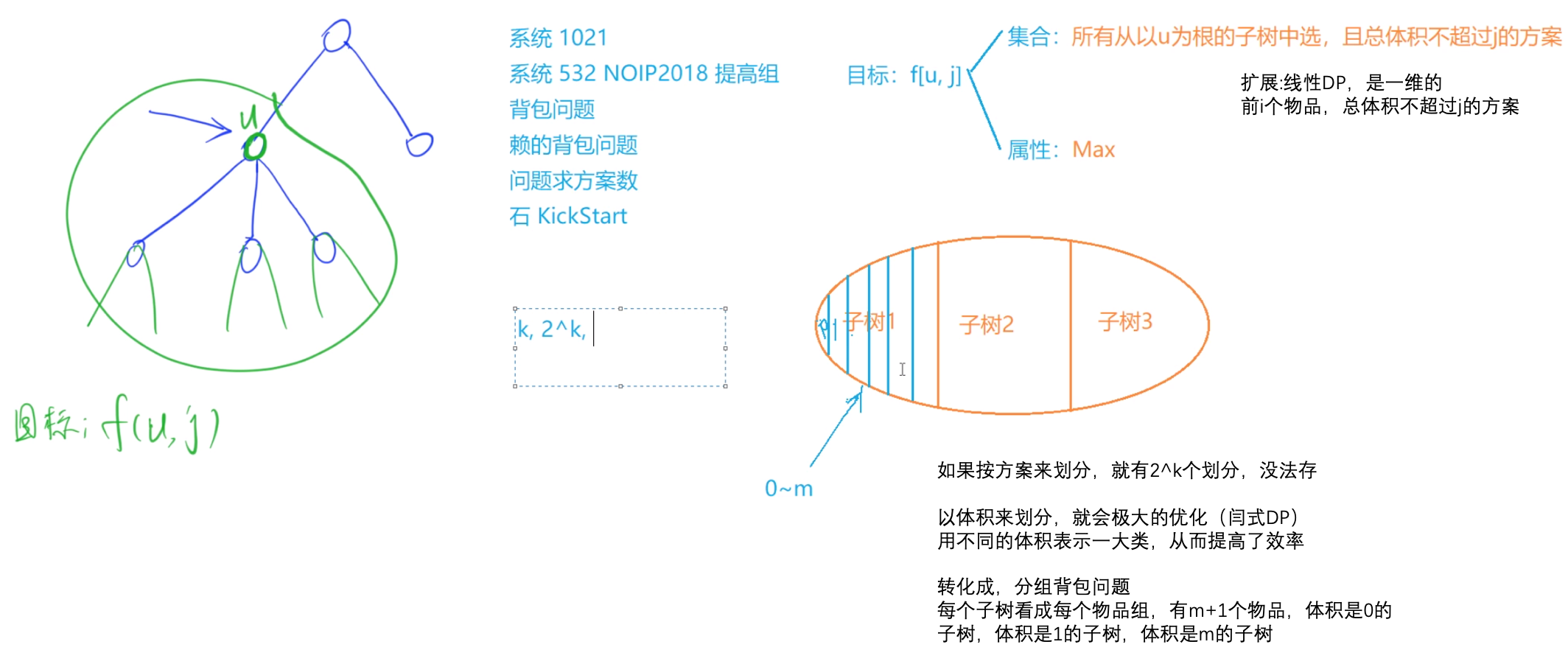
有依赖的背包问题

例题：1271：【例9.15】潜水员

#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int dp[N][25][90];
int v1[N], v2[N], w[N];
int n, m, s;
int main()
{
    cin >> n >> m >> s;
    for (int i = 1; i <= s; i++)
        cin >> v1[i] >> v2[i] >> w[i];
    memset(dp, 0x3f, sizeof dp);
    dp[0][0][0] = 0;
    for (int i = 1; i <= s; i++)
        for (int j1 = 0; j1 <= n; j1++)
            for (int j2 = 0; j2 <= m; j2++){
                dp[i][j1][j2] = dp[i - 1][j1][j2];
                dp[i][j1][j2] = min(dp[i][j1][j2], 
                                        dp[i - 1][max(0, j1 - v1[i])][max(0, j2 - v2[i])] + w[i]);
            }
    cout << dp[s][n][m] << '\n';
    return 0;
}

例题：有依赖的背包问题

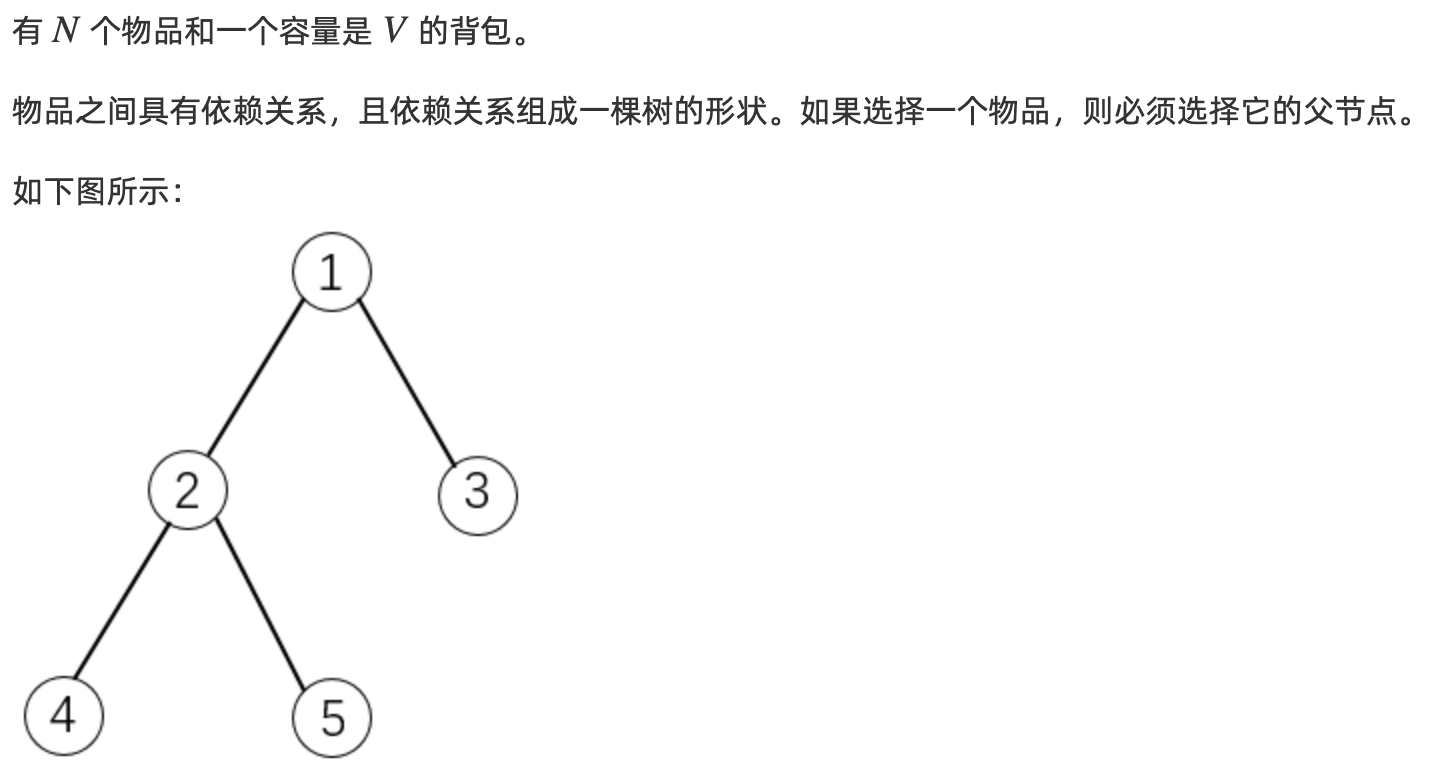
// 这种背包问题的物品间存在某种“依赖”的关系
// 也就是说，物品i 依赖于 物品j，表示若选 物品i，则必须选 物品j
// 为了简化起见，我们先设没有某个物品既依赖于别的物品，又被别的物品所依赖
// 另外，没有某件物品同时依赖多件物品。
// 需要会树的存储
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
int n, m;
int v[N], w[N];
int h[N], e[N], ne[N], idx;
int f[N][N];  //f[u][j] 所有从以u为根的子树中选，且总体积不超过j的方案
void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
// 框架是树形DP+每个结点递归的那层, 递归的思路
void dfs(int u)
{
    for (int i = h[u]; ~i; i = ne[i]) //循环物品组
    {
        int son = e[i];
        dfs(e[i]);
        //分组背包
        for (int j = m - v[u]; j >= 0; j--) //循环体积
            for (int k = 0; k <= j; k++)  //循环决策
                f[u][j] = max(f[u][j], f[u][j - k] + f[son][k]);
    }
    //将物品u加进去
    for (int i = m; i >= v[u]; i--) f[u][i] = f[u][i - v[u]] + w[u];
    for (int i = 0; i < v[u]; i++) f[u][i] = 0;
}
int main()
{
    cin >> n >> m;
    memset(h, -1, sizeof h);
    int root;
    for (int i = 1; i <= n; i++)
    {
        int p;
        cin >> v[i] >> w[i] >> p;
        if (p == -1) root = i;
        else add(p, i);
    }
    dfs(root);
    cout << f[root][m] << endl;
    return 0;
}
//如果按方案来划分，就有2^k个划分，没法存
//以体积来划分，就会极大的优化（闫式DP）
//用不同的体积表示一大类，从而提高了效率
//转化成，分组背包问题
//每个子树看成每个物品组，有m+1个物品，体积是0的子树，体积是1的子树，体积是m的子树

背包问题问法的变化

例题：背包问题求方案数

例题：背包问题求具体方案