L. Euler studied such paths in 1736 when he solved the famous Königsberg bridge problem. This was the birth of graph theory.(七桥问题)

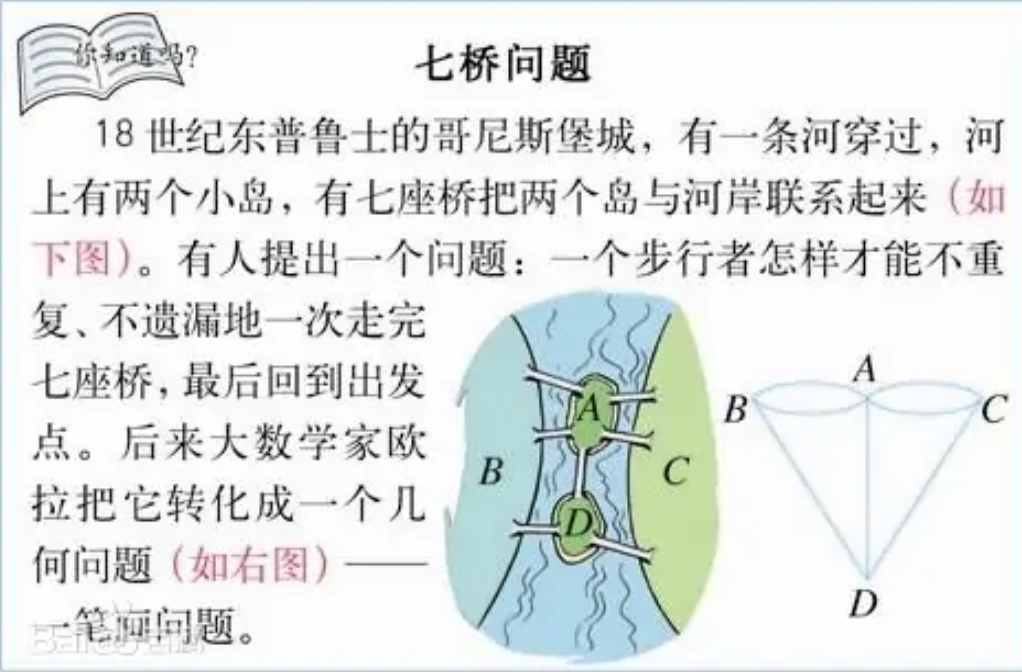
image.png
An Eulerian path(欧拉路径) is a path that goes exactly once through each edge of the graph. For example, the graph has an Eulerian path from node 2 to node 5:

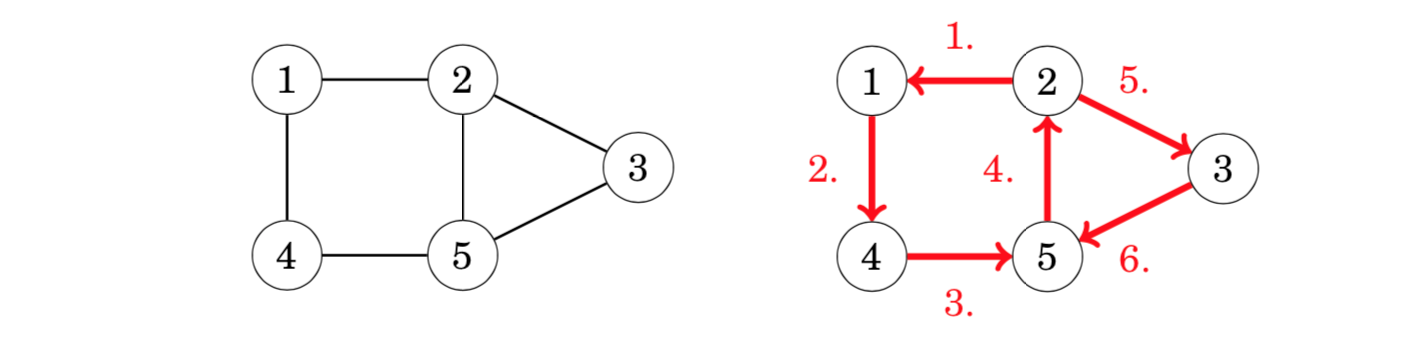
image.png

An Eulerian circuit(欧拉回路) is an Eulerian path that starts and ends at the same node. For example, the graph has an Eulerian circuit that starts and ends at node 1:

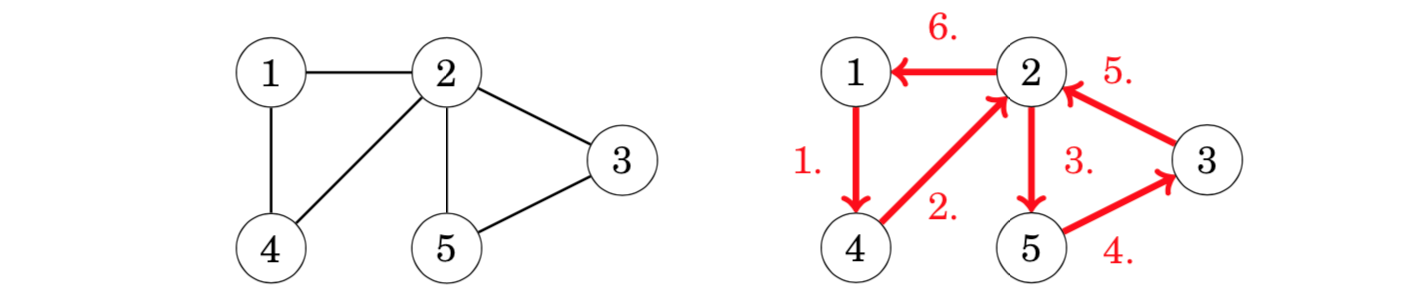
image.png

Existence

The existence of Eulerian paths and circuits depends on the degrees of the nodes. First, an undirected graph has an Eulerian path exactly when all the edges belong to the same connected component and

  • the degree of each node is even(所有点的度数是偶数)(欧拉回路)
  • the degree of exactly two nodes is odd, and the degree of all other nodes is even.(有两个点度数是奇数，其他所有点的度数是偶数)(欧拉路径)(奇数点就是起点)
  • 以上两点满足其一

In the first case, each Eulerian path is also an Eulerian circuit. In the second case, the odd-degree nodes are the starting and ending nodes of an Eulerian path which is not an Eulerian circuit.

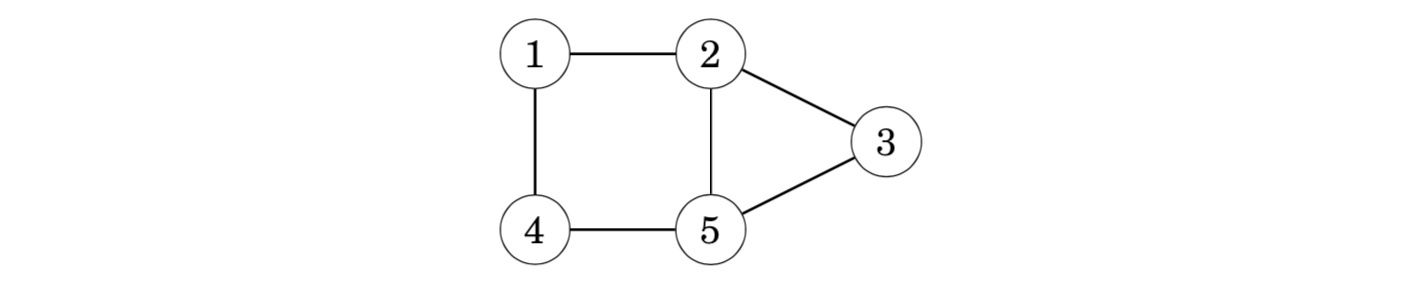
image.png

nodes 1, 3 and 4 have a degree of 2, and nodes 2 and 5 have a degree of 3. Exactly two nodes have an odd degree, so there is an Eulerian path between nodes 2 and 5, but the graph does not contain an Eulerian circuit.

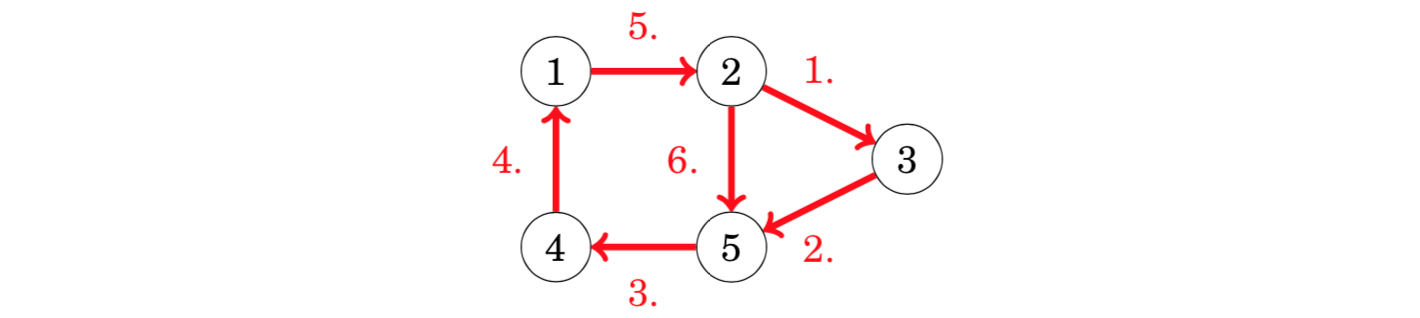
In a directed graph, we focus on indegrees and outdegrees of the nodes. A directed graph contains an Eulerian path exactly when all the edges belong to the same connected component and

  • in each node, the indegree equals the outdegree(所有点出度和入度相等)(欧拉回路)
  • in one node, the indegree is one larger than the outdegree, in another node, the outdegree is one larger than the indegree, and in all other nodes, the indegree equals the outdegree.(一个点入度比出点大1，一个点出点比入度大1，其他点入度和出度相等)(欧拉路径)
  • 以上两点满足其一

In the first case, each Eulerian path is also an Eulerian circuit, and in the second case, the graph contains an Eulerian path that begins at the node whose outdegree is larger and ends at the node whose indegree is larger.

image.png

nodes 1, 3 and 4 have both indegree 1 and outdegree 1, node 2 has indegree 1 and outdegree 2, and node 5 has indegree 2 and outdegree 1. Hence, the graph contains an Eulerian path from node 2 to node 5:

image.png

  1. //示例代码，一笔画问题
  2. #include <bits/stdc++.h>
  4. using namespace std;
  6. const int N = 110;
  8. int g[N][N], in[N];
  9. int n, m;
  10. vector<int> path;
  11. bool vis[N];
  12. int circuit = 0;
  14. void dfs(int u)
  15. {
  16.     path.push_back(u);
  18.     for (int j = 1; j <= n; j++)
  19.         if (g[u][j]){
  20.             g[u][j] = g[j][u] = 0; //这条边画掉
  21.             dfs(j);
  22.             break;
  23.         }
  24. }
  26. int main()
  27. {
  28.     cin >> n >> m;
  29.     for (int i = 0; i < m; i++){
  30.         int a, b;
  31.         cin >> a >> b;
  32.         g[a][b] = g[b][a] = 1;
  34.         in[a]++; in[b]++;
  35.     }
  37.     int st = 1;
  38.     for (int i = 1; i <= n; i++){
  39.         if (in[i] & 1) {st = i;break;}
  40.     }
  42.     dfs(st);
  44.     for (int i = 0; i < (int)path.size(); i++) printf("%d ", path[i]);
  45.     puts("");
  47.     return 0;
  48. }

例题，【例题】一笔画问题

  1. //寻找欧拉路/欧拉回路。
  2. //找到入度是奇数的点，这个点作为出发点。否则就从1开始出发
  3. //dfs()遍历图，一边走一遍划掉边

例题，铲雪车(snow)

  1. //每条道路都是双向道路，题面说明可以遍历所有街道，那一定是欧拉回路的
  2. //直接利用欧拉回路的性质解题
  3. //需要注意的是时间有可能很大，不开LL见祖宗

例题，骑马修栅栏(fence)

  1. //一笔画问题，一笔遍历完所有栅栏
  2. //完成建图后，从度数是奇数的点出发，进行dfs()，一边走一边抹掉边
  3. //题目中没有给出结点编号范围，在读入的时候，明确一下起始和终止结点编号