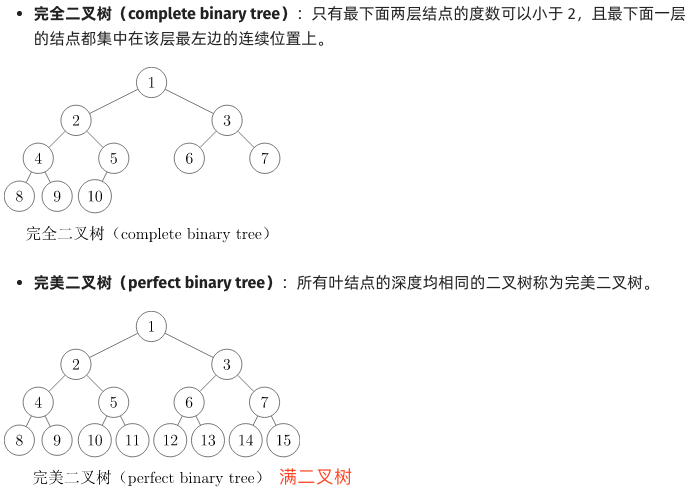
完全二叉树的定义与基本性质

image.png

完全二叉树的数组表示法

  • 对于一棵具有 n 个结点的完全二叉树，对于任意一个结点，编号为 i

if (i > 1) 父结点编号 i / 2
if (2 i > n) 没有左儿子 else 左儿子编号为 2 i
if (2 i + 1 > n) 没有右儿子 else 右儿子编号为 2 i + 1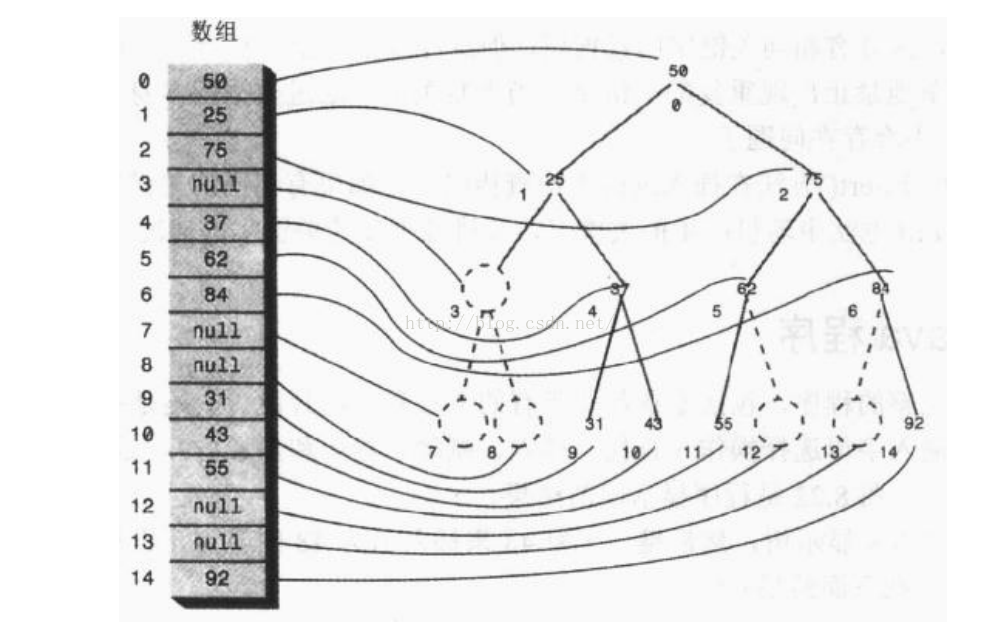
image.png

  1. #include <bits/stdc++.h>
  3. using namespace std;
  5. const int N = 1010;
  7. char data[N];
  8. int node[N];
  9. int n;
  11. void pre_order(int i){
  12.     if (data[i] == '$') return ;
  14.     if (data[i] != '$') cout << data[i];
  15.     if (i * 2 <= n) pre_order(i * 2);
  16.     if (i * 2 + 1 <= n) pre_order(i * 2 + 1);
  17. }
  19. void in_order(int i){
  20.     if (data[i] == '$') return ;
  22.     if (i * 2 <= n) in_order(i * 2);
  23.     if (data[i] != 'S') cout << data[i];
  24.     if (i * 2 + 1 <= n) in_order(i * 2 + 1);
  25. }
  27. void post_order(int i){
  28.     if (data[i] == '$') return ;
  30.     if (i * 2 <= n) post_order(i * 2);
  31.     if (i * 2 + 1 <= n) post_order(i * 2 + 1);
  32.     if (data[i] != 'S') cout << data[i];
  33. }
  35. int main(){
  36.     memset(data, '$', sizeof data);
  38.     cin >> n;         // 结点总数
  39.     for (int i = 1; i <= n; i++) cin >> data[i];  // 根结点下标是1，从上到下，从左到右输入
  41.     pre_order(1);
  42.     puts("");
  44.     in_order(1);
  45.     puts("");
  47.     post_order(1);
  48.     puts("");
  50.     return 0;
  51. }
  53. /*
  54. 输入：
  55. 3
  56. A B C
  58. 输出：
  59. ABC
  60. BAC
  61. BCA
  62. */

哈夫曼树的定义、构造及其遍历

定义

Huffman Tree， 给定n个权值作为n个叶子结点，构造一棵二叉树，若该树的WPL(带权路径)长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。

构造

在我们已有的权值（例子里的频次）中，每次都找到2个最小的，将它们构造成一颗二叉树，再插入我们已经构造好的二叉树中，将每个值都插完后，我们的哈夫曼树就构造完成了。
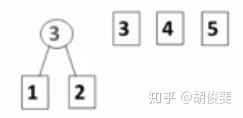
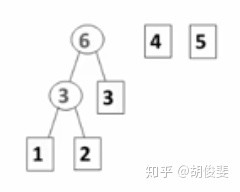
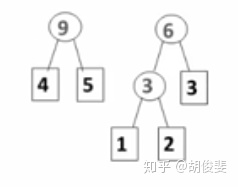
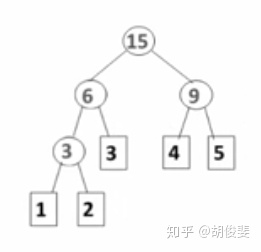
image.png
image.png
image.png
image.png
image.png
那我们的代码如何实现呢？如果我们要按如上的方法实现哈夫曼树，首先我们要找到的就是最小值，如何找到最小值一定是我们需要面对的最关键的问题。这里有2种方法：
1、先将所有的权值排序，如何再建立哈夫曼树。
2、先建立最小堆，每次从堆顶选元素来建立哈夫曼树。

遍历

  1. //

二叉查找树的定义、构造及其遍历

定义

二叉排序树（Binary Sort Tree），又称二叉查找树（Binary Search Tree），亦称二叉搜索树。

二叉排序树或者是一棵空树，或者是具有下列性质的二叉树：
（1）若左子树不空，则左子树上所有结点的值均小于它的根结点的值；
（2）若右子树不空，则右子树上所有结点的值均大于它的根结点的值；
（3）左、右子树也分别为二叉排序树；
（4）没有键值相等的节点。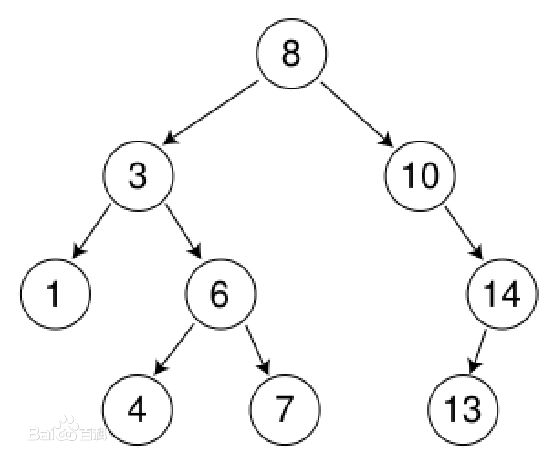
image.png

构造

假设我们要为数组 a[] = {10 ， 5 ， 15 ， 6 ， 4 ， 16 }构建一个二叉排序树，我们按顺序逐个插入元素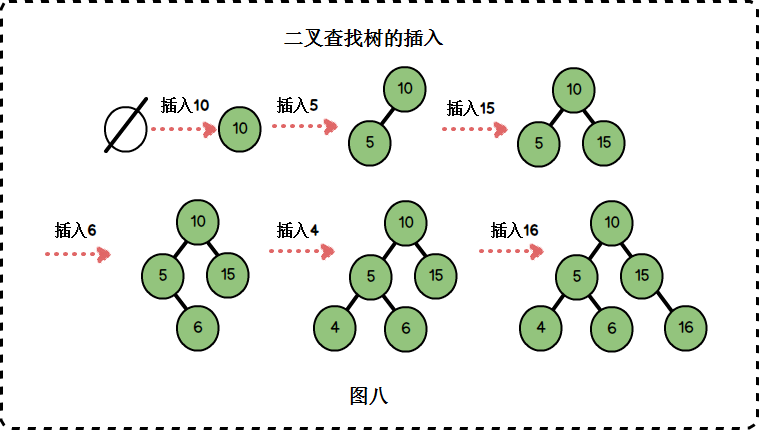
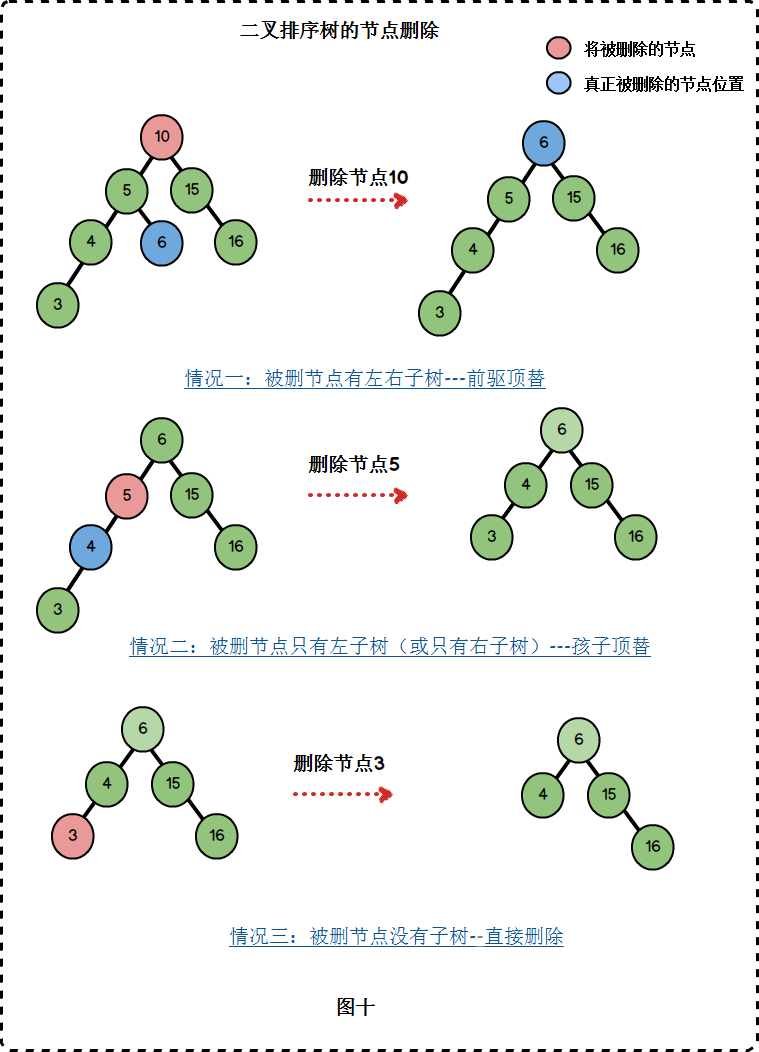
image.png
image.png

前驱节点val值小于该节点val值并且值最大的节点
后继节点val值大于该节点val值并且值最小的节点

遍历

查找指定元素的节点（While循环)：

  1. 判断当前结点是否为空指针，不是空指针进入
  3. key直接和当前结点value相等，return当前结点
  5. key大于当前结点value，将右子节点赋予当前结点
  7. key小于当前结点value，将左子节点赋予当前结点
  9. 直到key等于当前结点或者当前结点为空停止while循环
  1. // NOIP2013普及组初赛
  3. #include <iostream> 
  5. using namespace std; 
  7. const int SIZE = 100;
  8. const int INFINITE = 1000000;
  10. struct node{
  11.     int left_child, right_child, value;
  12. }a[SIZE];
  14. int is_bst( int root, int lower_bound, int upper_bound ){
  15.     int cur;
  16.     if (root == 0) return 1;
  18.     cur = a[root].value;
  19.     if ((cur > lower_bound) && (cur < upper_bound) && 
  20.         (is_bst(a[root].left_child, lower_bound, cur) == 1) && 
  21.         (is_bst(a[root].right_child, cur, upper_bound) == 1) )
  22.         return 1;
  24.     return 0;
  25. }
  27. int main()
  28. {
  29.     int i, n; 
  30.     cin >> n;
  31.     for (i = 1; i <= n; i++)
  32.         cin >> a[i].value >> a[i].left_child >> a[i].right_child;
  34.     cout << is_bst(1, -INFINITE, INFINITE) << endl;
  36.     return 0;
  37. }

例题

例题，FBI树(fbi)

  1. void dfs(int l, int r)
  2. {
  3.     //边界
  5.     //子问题
  6.     int len = (r - l) / 2;
  7.     dfs(l, l + len);
  8.     dfs(l + len + 1, r);
  10.     //按题意模拟操作
  11. }

例题，对称二叉树(tree_c)

  1. //思路1，从s[1]开始，两两为一单位，要么都是#，要么都不是#
  2. //思路2，根据左儿子和右儿子的位置，去判断左右儿子要么同时为#，要么同时不是#
  3. //两个思路，都需要在读入的字符串后面加上一个#，避免最后一个叶子结点没有兄弟的情况

大纲要求

•【4】完全二叉树的定义与基本性质

•【4】完全二叉树的数组表示法

•【4】哈夫曼树的定义、构造及其遍历

•【4】二叉树的定义、构造及其遍历