动态规划的基本思路【4】
- 问题：数塔问题（动态规划算法基本原理）
  - 【例9.2】数字金字塔">例题，【例9.2】数字金字塔
简单一维动态规划【4】
简单背包类型动态规划【5】
- 问题：01背包(Subset Sum)
  - 【例9.11】01背包问题">例题，【例9.11】01背包问题
  - 装箱问题">例题，装箱问题
问题：数塔问题加强版01
- 【例9.21】方格取数">例题，【例9.21】方格取数
问题：数塔问题加强版02
问题：数塔问题加强版03
简单区间类型动态规划【5】
- 问题，石子合并
  - 【例9.18】合并石子">例题，【例9.18】合并石子
大纲要求
例题代码

本章面向大纲展开，以几个经典问题展开，伴随引导问题进行思考
真正认识动态规划，而不是仅仅背模板
经典问题包括： 数字三角形，LIS，LCS，石子合并

动态规划的基本思路【4】

在信息学竞赛中，第一次考查动态规划是在 IOI 1994（国际信息学竞赛）中的“数塔问题”，虽然当时全世界信息学顶尖选手的此题得分率极低，但是现在已经作为DP算法的入门题出现。其模型比较直观，有助于我们理解动态规划算法中的相关概念和性质。

很多老师在讲授动态规划时，先罗列相关非常生涩的概念，很多学生无法真正理解，下面我们从一个相对直观的问题出发，一步一步引导学生去主动思考，在解决问题的过程中，学生可以理解问题的本质。

问题：数塔问题（动态规划算法基本原理）

有一些数字排成数塔的形状，
其中第一层有一个数字，第二层有两个数字，……，第n层有n个数字。
现在要从第一层走到第n层，每次只能选择左下方或者右下方的数字，
问：“最后将路径上所有数字相加后得到的和最大是多少？”

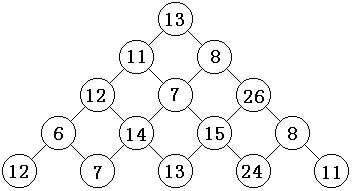
动态规划第1讲 - 图1

引导思考：

（1）从起点到第一行第一列的答案是固定的。
（2）在第一步骤基础上，从起点到第二行的答案也是固定的。
（3）在第三行时，7 有两种选择，显然会选择累积更大的 8 过来才是最优的
    若将f[i][j]定义为从第一行第一列到第 i 行第 j 列的路径上的数字和的最大值，
    则到 数字7 的递推式为：f[3][2] = max(f[2][1],f[2][2]) + 7
（4）可得出一般递推式为 f[i][j] = max(f[i-1][j-1], f[i-1][j]) + a[i][j]
    我们只需要推到第n行，就可以得到ans = max{f[n][1…n]}

解法提炼：

（1）状态定义：
    f[i][j]定义从第一行第一列到第 i 行第 j 列的路径上的数字和的最大值
（2）所求：
    max{f[n][1…n]}
（3）状态转移：
    f[i][j]=max(f[i-1][j-1],f[i-1][j]) + a[i][j]

正确性分析：

（1）前面推导的结果不会随着后几行得到的结果而改变——无后效性。
（2）局部最优可以保证全局最优——最优子结构。
    这两个性质也是动态规划算法解决问题的先决条件。

// 数字三角形示例代码
#include <bits/stdc++.h>
using namespace std;
const int N = 510;
int a[N][N], dp[N][N], n;
int main(){
    cin >> n;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= i; j++) cin >> a[i][j];
    // 填表法
    memset(dp, -0x3f, sizeof dp);
    dp[1][1] = a[1][1];
    for (int i = 2; i <= n; i++)
        for (int j = 1; j <= i; j++){
            dp[i][j] = max(dp[i][j], dp[i - 1][j] + a[i][j]);
            if (j > 1) dp[i][j] = max(dp[i][j], dp[i - 1][j - 1] + a[i][j]);
        }
    int ret = -2e9;
    for (int j = 1; j <= n; j++) ret = max(ret, dp[n][j]);
    cout << ret << '\n';
    return 0;
}

例题，【例9.2】数字金字塔

//数字三角形模型

简单一维动态规划【4】

问题：最长上升子序列问题(动态规划的状态定义)

给定一个长度为 n 的数字序列，求最长的上升子序列长度。
如3、1、2、6、4、5的最长上升子序列为1、2、4、5，故答案为4。

在数塔问题的基础上，很容易想到如下解法：

（1）状态定义：
    f[i] 定义为到第 i 个数字为止，能获得最长子序列长度
（2）所求：
    f[n]
（3）状态转移：
    显然很难寻找到 f[i] 关于 f[1…i-1] 的递推关系。

无法找到递推关系是由于递推时的大小关系需要明确第 i 个数与前面某个确定的数进行比较，而原有的状态定义无法获得哪些数字被选中，故无法直接进行比较，带着这个问题，容易想到新的解法：

（1）状态定义：
    f[i] 定义为到第 i 个数字为止，
    且第 i 个数必须为该子序列的最后一个数字时，所获得的最长子序列的长度。
（2）所求：
    max{f[1…n]}
（3）状态转移：
    f[i] = max{f[j] + 1} | 1 <= j <= i-1, a[j] < a[i]。

该算法的时间复杂度为O(n^2)，空间复杂度为O(n)。

// LIS示例代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
int a[N], n;
int dp[N], ret;
int main(){
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    // 填表法
    a[0] = -2e9, dp[0] = 0;
    for (int i = 1; i <= n; i++)             // 枚举以i为结尾
        for (int j = 0; j < i; j++)          // 枚举从哪个数来
            if (a[j] < a[i]) dp[i] = max(dp[i], dp[j] + 1); 
    for (int i = 1; i <= n; i++) ret = max(ret, dp[i]);
    cout << ret << '\n';
    return 0;
}

例题，最长上升子序列

//LIS

问题：最长公共子序列问题

给定两个长度为 n 的数字序列，求最长的公共子序列长度。
第一个数字序列为 1、6、2、5、4、7，
第二个数字序列为 1、2、5、5、2、7，
则最长的公共子序列为1、2、5、7，其长度为4。

顺着LIS的思路，可以得到如下解法。
（1）状态定义：
    f[i][j] 定义为当第一行数字取到第 i 个，第二行数字取到第 j 个时，
    所能得到的最长公共子序列长度，
    且第 i 个数字和第 j 个数字分别为所求子序列的最后一个数字（即这两个数字必须取到）
（2）所求：
    max{f[1…n][1…n]}
（3）状态转移：
    f[i][j] = 0      | a[i] ≠ b[j] 
    max(f[p][q]) + 1 | a[i] = b[j], a[p] = b[q]

该解法状态总数共有n^2个，
每个状态需要枚举i和j前面所有的p和q，求解单个状态需要的枚举量为(i-1)*(j-1)，
其时间复杂度是O(n^2)，
总共有n^2个状态，故总的时间复杂度为O(n^4)，空间复杂度为O(n^2)。

该算法的瓶颈主要在于求解每个状态都需要去枚举前面所有的状态，
下面我们尝试使用另外一种状态定义。

（1）状态定义：
    f[i][j] 定义为当第一行数字取到第 i 个，第二行数字取到第 j 个时，
    所能得到的最长子序列长度，
    且第 i 个数字和第 j 个数字不需要为所求子序列的最后一个数字（即这两个数字取到与否都可以）
（2）目标：
    f[n][n]
（3）状态转移：
    f[i][j] = f[i-1][j-1] + 1           | a[i] = b[j] 
              max(f[i-1][j], f[i][j-1]) | a[i] ≠ b[j]

当 a[i] 与 b[j] 相等时，其会对目标值贡献 +1，
而 a[i] 与 b[j] 不相等时，显然这两个数字无法配对，
故对 f[i][j] 而言，a[i] 和 b[j] 中必有一个是多余的，
故 f[i][j] = max(f[i-1][j], f[i][j-1])
此时计算f[i][j]的时间复杂度为O(1)，故总的时间复杂度为O(n^2)。

例题，【例9.9】最长公共子序列

//LCS

问题：最大子段和问题

Given an array of n numbers, our task is to calculate the maximum subarray sum.
//举例
-1  2  4  -3  5  2  -5  2
//最大子段和是10
    2  4  -3  5  2

Consider the subproblem of finding the maximum-sum subarray that ends at position k. There are two possibilities:

1. The subarray only contains the element at position k.
2. The subarray consists of a subarray that ends at position k − 1,
   followed by the element at position k.

In the latter case, since we want to find a subarray with maximum sum, the subarray that ends at position k − 1 should also have the maximum sum. Thus, we can solve the problem efficiently by calculating the maximum subarray sum for each ending position from left to right.

int best = 0, sum = 0;
for (int k = 0; k < n; k++) {
    sum = max(array[k],sum+array[k]);
    best = max(best,sum);
}
cout << best << "\n";

// 完整的示例代码 v1
#include <bits/stdc++.h>
using namespace std;
int a[20], n;
int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    int maxn = -0x3f3f3f3f, area = 0;
    for (int i = 1; i <= n; i++){
        area += a[i];
        if (area > maxn) maxn = area;
        if (area < 0) area = 0;  //另起炉灶
    }
    cout << maxn << '\n';
    return 0;
}

// 完整的示例代码 v2
#include <bits/stdc++.h>
using namespace std;
int a[20], n;
int dp[20];
int maxn = -0x3f3f3f3f;
int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int i = 1; i <= n; i++){
        dp[i] = max(dp[i - 1], 0) + a[i];     //另起炉灶
        maxn = max(maxn, dp[i]);    
    }
    cout << maxn << '\n';
    return 0;
}

简单背包类型动态规划【5】

问题：01背包(Subset Sum)

有 n 件物品和一个容量是 m 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi，价值是 wi。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

（1）状态定义：
    f[i][j] 定义为放到第i个物品为止，体积为j的最大价值
（2）目标：
    f[n][m]
（3）状态转移：
    f[i][j] = f[i - 1][j]               , 不选第i个物品
    f[i][j] = f[i - 1][j - v[i]] + w[i], 选第i个物品

例题，【例9.11】01背包问题

//01背包

例题，装箱问题

//任取若干个装入箱内，使箱子的剩余空间为最小
//01背包，输出V-dp[V]

问题：数塔问题加强版01

“加一维”思想在动态规划问题中的应用

在问题一的基础上，增加一个条件：
有且仅有一次机会可以将路径中的一个数字获得两次，求最后路径中路径上数字的和的最大值。

题目描述
有一些数字排成数塔的形状，其中第一层有一个数字，第二层有两个数字，……，第n层有n个数字。
现在要从第一层走到第n层，每次只能选择左下方或者右下方的数字，
有一张特权卡，只有一次使用机会，可以对当前数字取两次。
问：“最后将路径上所有数字相加后得到的和最大是多少？”
输入数据：
第一行，三个整数，n, x, y
后面每行为这个数字金字塔特定行包含的整数（数据保证输入的数都是非负数）
输入数据样例1：
3
1
1 2
1 1 1
输出数据样例1：
6
输入数据样例2：
3
1
1 8
14 8 8
输出数据样例2：
30
输入数据样例3：
3
1
1 10
11 10 10
输出数据样例3：
31
提示：
n <= 1e3, 0 <= a[i][j] <= 100

显然存在几种明显错误的贪心思想：
（1）在问题一基础上，对路径中最大的数字使用额外取一次的机会。
可构造如下反例：
1
1 8
14 8 8
经过问题一的处理，会发现路径为1-8-8，再对路径中最大值8额外取一次，最后结果为25，而显然存在更优的答案为1-1-14，其最后的结果为30。

（2）有了上述反例，又尝试进行如下的贪心策略：将所有数字中最大的数字选定，再以这个数字为起点往上取到顶，往下取到最后一行。又可构造反例如：
1
1 10
11 10 10
按照贪心策略，其路径为1-1-11，结果为24，而存在答案为1-10-10，31。

显然两种贪心策略刚好互为反例，无法兼顾，而如果在考场上仅仅为了获得更多的分数，可以采取将两种贪心策略分别计算，最后取两者中的最优值来进行骗分。

而正确做法就是本文要提出的“加一维”解法！

引导思考：

（1）在不使用额外机会时，与 数字三角形问题 是完全一样的。
（2）机会使用后，也与 数字三角形问题 是完全一样的。
（3）每个数字都有使用该机会的可能性。

提出解法：

（1）状态定义：
    f[i][j][k] 定义为取到第 i 行第 j 列时，
    机会的状态是 k 时能获得的目标值最优为多少，
    k 为 0 表示机会已经使用，k 为 1 表示机会尚未使用。
（2）所求：
    max(f[n][1..n][0])
（3）状态转移：
    如果在第 i 行第 j 列时，机会依旧存在，则在此之前其机会也必须存在
    故递推式为：
    f[i][j][1] = max(f[i-1][j-1][1], f[i-1][j][1]) + a[i][j]
    如果机会已经被使用，则f[i][j][0]有两种可能性：
    在此之前机会已经被使用 max(f[i-1][j-1][0], f[i-1][j][0]) + a[i][j]
    或者对a[i][j]使用取两次的机会max(f[i-1][j-1][1], f[i-1][j][1]) + 2 * a[i][j]，
    我们只需在这两种可能性中取最大值便可。

我们通过加入该机会是否被使用的状态作为新的一维，枚举其转移时的所有可能性，巧妙的解决了该问题，且时间复杂度和空间复杂度依旧和原问题同阶。

这种技巧也在大量的动态规划问题中适用，当我们无法很轻松的将“不可控的量”交代清楚时，可以将其状态作为单独的一维代入计算。

例题，【例9.21】方格取数

// 这道题目，也是一个加强版
// 走两遍
// 从左上走到右下，走了两次，问能取到的最大值
// 定义一个四维的状态，dp[N][N][N][N]，
// 经过发现，可以优化到三维

问题：数塔问题加强版02

一种trick，挺巧妙

题目描述
有一些数字排成数塔的形状，其中第一层有一个数字，第二层有两个数字，……，第n层有n个数字。
现在要从第一层走到第n层，每次只能选择左下方或者右下方的数字，
经过的路径，必须经过指定的位置(x, y)
问：“最后将路径上所有数字相加后得到的和最大是多少？”
输入数据：
第一行，三个整数，n, x, y
后面每行为这个数字金字塔特定行包含的整数（保证输入的数据都是非负数）
输入数据样例：
3 2 1
1
1 2
1 1 1
输出数据样例：
3
提示：
n <= 1e3, 0 <= a[i][j] <= 100

问题：数塔问题加强版03

01 + 02 = 03

题面描述
有一些数字排成数塔的形状，其中第一层有一个数字，第二层有两个数字，……，第n层有n个数字。
现在要从第n层走到第1层，每次只能选择左上方方或者右上方的数字，
两个限制条件：
1、经过的路径，必须经过指定的位置(x, y)
2、有一张特权卡，只有一次使用机会，可以对当前数字取两次
问：“最后将路径上所有数字相加后得到的和最大是多少？”
输入数据：
第一行，三个整数，n, x, y
后面每行为这个数字金字塔特定行包含的整数（保证输入的数据可能是负数）
输出数据：
一个整数，经过(x, y)走到第一行，数字之和的最大值
输入数据样例：
5 3 2
7
3 -8
8 1 0
2 7 4 4
4 5 2 6 5
输出数据样例：
30
提示：
注意，数字三角形中的数据，可能都是负数
n <= 1e3, -1e7 <= a[i][j] <= 1e7

简单区间类型动态规划【5】

问题，石子合并

题目描述：
在一个操场上一排地摆放着Ｎ堆石子。
现要将石子有次序地合并成一堆。
规定每次只能选相邻的２堆石子合并成新的一堆，并将新的一堆石子数记为该次合并的得分。
计算出将Ｎ堆石子合并成一堆的最小得分。

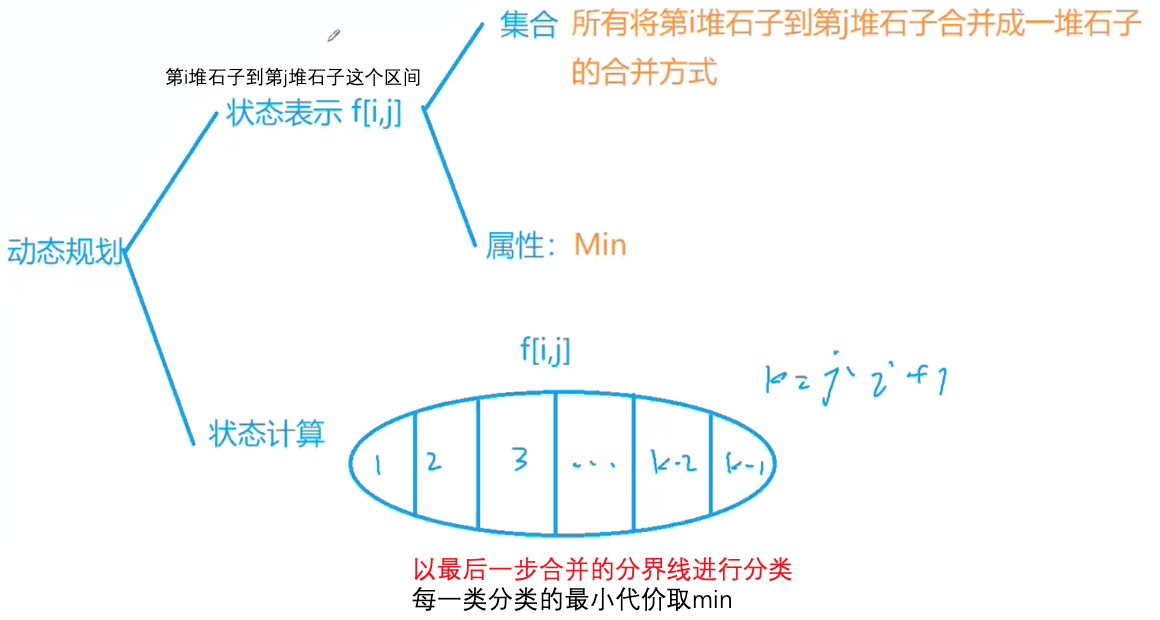
若最初的第 l 堆石子和最初的 第 r 堆石子被合并成一堆，则说明 l~r 之间的每堆石子也已经被合并，
这样，l 和 r 才有可能相邻。
[l, r]表示这堆石子是由最初的第 l~r 堆石子合并而成的
则一定才在一个整数k，l <= k < r
在[l, r]这堆石子形成之前，先有的[l, r]被合并成一堆，[k+1, r]被合并成一堆，
然后，这两堆石子才能合并成[l, r]

对应到动态规划中，两个长度较小的区间上的信息向一个更长的区间发生了转移，
划分点 k 就是转移的决策。
自然地，应该把区间长度 len 作为DP的阶段。
因为区间长度可以由左端点和右端点表示出，即 len = r - l + 1
在设计状态的时候，本着“选择最小的能覆盖状态空间的维度集合”的思想，只用左、右端点表示DP的状态。
不是f[len][l][r], 而是f[l][r]
状态定义
f[l][r]表示把最初的第 l 堆到第 r 堆石子合并成一堆，需要消耗的最少体力
初始状态
f[i][i] = a[i]
状态转移方程
f[l, r] = min{f[l, k] + f[k + 1, r]} + sum of [l, r]  | l <= k < r
目标
f[1][n]

在编程实现动态规划的状态转移方程时， 务必分清阶段、状态与决策，三者应按照从外到内的顺序依次循环

例题，【例9.18】合并石子

#include <bits/stdc++.h>
using namespace std;
const int N = 310;
int a[N], s[N], n;
int f[N][N];  // f[i][j]表示合并[i,j]区间的石子需要耗费的体力
int main(){
    cin >> n;
    for (int i = 1; i <= n; i++){
        cin >> a[i];
        s[i] = s[i - 1] + a[i];
    }
    memset(f, 0x3f, sizeof f);
    for (int i = 1; i <= n; i++) f[i][i] = 0;   // 自己一个的时候，不用合并，耗费是0
    for (int len = 2; len <= n; len++)          // 阶段，有两个石子才发生合并的行为
        for (int i = 1; i <= n - len + 1; i++){ // 状态 左端点i
            int j = i + len - 1;                // 状态 右端点j
            for (int k = i; k < j; k++)         // 决策
                f[i][j] = min(f[i][j], f[i][k] + f[k + 1][j]);
            f[i][j] += s[j] - s[i - 1];
        }
    cout << f[1][n] << '\n';    
    return 0;
}

大纲要求

【4】动态规划的基本思路

【4】简单一维动态规划

【5】简单背包类型动态规划

【5】简单区间类型动态规划

例题代码

// LCS O(n^4)
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
char a[N], b[N];
int n, m;
int f[N][N];
int main(){    
    scanf("%s", a + 1);
    scanf("%s", b + 1);
    n = strlen(a + 1), m = strlen(b + 1);
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            if (a[i] == b[j]) f[i][j] = 1;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++){
            for (int p = 1; p < i; p++)
                for (int q = 1; q < j; q++){
                    if (a[i] == b[j] && a[p] == b[q])
                        f[i][j] = max(f[i][j], f[p][q] + 1);
                }
        }
    int ret = 0;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            ret = max(ret, f[i][j]);
    cout << ret << '\n';
    return 0;
}

// 数塔问题加强版01
// 有一个特权卡，可以在其中一个点取两次 
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int f[N][N][2];  // f[i][j][0]表示走到[i][j]使用了特权，f[i][j][1]表示走到了[i][j]还没使用特权
int a[N][N], n;
int main(){
    cin >> n;
    for (int i = 1; i <= n; i++)    
        for (int j = 1; j <= i; j++) cin >> a[i][j];
    f[1][1][0] = a[1][1] * 2, f[1][1][1] = a[1][1];
    for (int i = 2; i <= n; i++)
        for (int j = 1; j <= i; j++){
            f[i][j][1] = max(f[i-1][j][1], f[i-1][j-1][1]) + a[i][j];
            f[i][j][0] = max(max(f[i-1][j][0], f[i-1][j][0]) + a[i][j], max(f[i-1][j-1][1], f[i-1][j][1]) + a[i][j]*2);
        }
    int ret = -0x3f3f3f3f;
    for (int j = 1; j <= n; j++) ret = max(ret, f[n][j][0]);
    cout << ret << '\n';
    return 0;
}

// 数塔问题加强版02 数据都是正数，a[i][j] < 100
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int n, x, y;
int a[N][N], f[N][N];
int main(){
    cin >> n >> x >> y;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= i; j++) cin >> a[i][j];
    a[x][y] += 1e9;    // 在(x,y)这个位置加上一个极大值，那么肯定会走这个点，必须的必
    f[1][1] = a[1][1];
    for (int i = 2; i <= n; i++)
        for (int j = 1; j <= i; j++)
            f[i][j] = max(f[i-1][j], f[i-1][j-1]) + a[i][j];
    int ret = 0;
    for (int j = 1; j <= n; j++) ret = max(ret, f[n][j]);
    cout << ret - 1e9 << '\n';
    return 0;
}

// 数塔问题加强版03 第一个版本
// 有一个特权卡，可以在其中一个点取两次 
// 从下往上递推
// [x,y]必须走
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1010;
ll f[N][N][2];  // f[i][j][0]表示走到[i][j]使用了特权，f[i][j][1]表示走到了[i][j]还没使用特权
ll f2[N][N][2];
ll a[N][N];
int x, y, n;
int main(){
    cin >> n >> x >> y;
    for (int i = 1; i <= n; i++)    
        for (int j = 1; j <= i; j++) cin >> a[i][j];
    // 把x那行，非[x,y]的点，全都置成极小值，这样就不会走其他的点，从而肯定会走[x,y]
    for (int j = 1; j <= x; j++) if (j != y) a[x][j] = -1e17;  
    for (int j = 1; j <= n; j++) f[n][j][0] = a[n][j] * 2, f[n][j][1] = a[n][j];
    for (int i = n - 1; i >= 1; i--)
        for (int j = 1; j <= i; j++){
            f[i][j][1] = max(f[i+1][j][1], f[i+1][j+1][1]) + a[i][j];
            f[i][j][0] = max(
                    max(f[i+1][j][0], f[i+1][j+1][0]) + a[i][j],
                    max(f[i+1][j][1], f[i+1][j+1][1]) + a[i][j]*2
                    );
        }
    ll ret = max(f[1][1][0], f[1][1][1]);  // 数据当中有可能都是负数，不使用特权卡更好一点
    cout << ret << '\n';
    return 0;
}
/*
5 3 2
7
3 -8
8 1 0
2 7 4 4
4 5 2 6 5
30
*/

// 数塔问题加强版03 第二个版本
// 有一个特权卡，可以在其中一个点取两次 
// 从下往上递推
// 必须经过[x,y]
// 分成两个部分，第一部分先从第n行爬到第x行，得到f[x][y][0] f[x][y][1]
// 第二部分，从x-1行往顶部继续爬，使用新的f2[][][]数组存储数据，f[x][y][0/1]作为现在的初始状态
// 从而保证必须进过[x,y]点，爬到[1,1]
// 另外，数据可能有炸，都是负数，最后可能不用特权卡更好一点
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1010;
// f[i][j][0]表示走到[i][j]使用了特权，f[i][j][1]表示走到了[i][j]还没使用特权
ll f[N][N][2];
ll f2[N][N][2];
ll a[N][N];
int n, x, y;
int main(){
    memset(f, 0xcf, sizeof f);
    memset(f2, 0xcf, sizeof f2);
    cin >> n >> x >> y;
    for (int i = 1; i <= n; i++)    
        for (int j = 1; j <= i; j++) cin >> a[i][j];
    for (int j = 1; j <= n; j++) f[n][j][0] = a[n][j] * 2, f[n][j][1] = a[n][j];
    for (int i = n - 1; i >= x; i--)
        for (int j = 1; j <= i; j++){
            f[i][j][1] = max(f[i+1][j][1], f[i+1][j+1][1]) + a[i][j];
            f[i][j][0] = max(
                    max(f[i+1][j][0], f[i+1][j+1][0]) + a[i][j],
                    max(f[i+1][j][1], f[i+1][j+1][1]) + a[i][j]*2
                    );
        }
    f2[x][y][0] = f[x][y][0], f2[x][y][1] = f[x][y][1];
    for (int i = x - 1; i >= 1; i--)
        for (int j = min(i, y); j >= 1; j--){
            f2[i][j][1] = max(f2[i+1][j][1], f2[i+1][j+1][1]) + a[i][j];
            f2[i][j][0] = max(
                    max(f2[i+1][j][0], f2[i+1][j+1][0]) + a[i][j],
                    max(f2[i+1][j][1], f2[i+1][j+1][1]) + a[i][j]*2
                    );
        }
    cout << max(f2[1][1][0], f2[1][1][1]) << '\n';
    return 0;
}
/*
5 3 2
7
3 -8
8 1 0
2 7 4 4
4 5 2 6 5
30
*/

动态规划 第1讲