本章面向经典问题，给出记忆化写法和循环迭代写法，对比转换
介绍DP的相关专业术语
本章的内容，相对比较简单

动态规划相关术语《进阶指南》

学习动态规划的阶段，容易产生这样的现象：看题没思路，看题解这么简单，抄TMD，下一题，怎么还是不会。循环往复。

所以在学习的时候，切莫呆板的去背模板，抄题解。

正所谓，模板不是用来背的，题解也不是用来Ctrl-c Ctrl-v的。

// 解决dp问题的基本路径
问题（形式化的表述）
|
v
方案的初始状态
|
v
中间状态
|
v
中间状态
|
v
目标（可行方案 / 最优解）

// 从搜索出发，看搜索推导的时候，有哪些状态未涉及到，哪些可以成为代表信息作为新的状态
// 这是最核心的思路来源
1.定义状态(存什么，哪些是全局变量，哪些是参数，哪些是局部变量)
2.简化状态(用最少的值去代表一个状态)
3.推导(怎么从一个状态搜到下一个状态)

我们之前探讨过的很多算法，都是利用问题的可划分性以及子问题之间的相似性来进行归纳，降低求解的复杂度，动态规划也不例外。动态规划把原问题视作若干个重叠子问题的逐层递进，每个子问题的求解过程都构成一个“阶段”。在完成前一个阶段的计算后，动态规划才会执行下一阶段的计算。

从“状态空间”入手对“问题与状态空间”之间的类比，有了更深入的认识。

递推和递归是两种遍历状态空间的基本方法
搜索算法，处理指数级别等非多项式复杂度的问题
动态规划算法，针对满足特定条件的一类问题，对各状态维度进行分阶段、有顺序、无重复、决策性的遍历求解

动态规划，把原问题视作若干个重叠子问题的逐层递进，每个子问题的求解过程都构成一个“阶段”。

在完成前一个阶段的计算后，动态规划才会执行下一阶段的计算。

为了保证这些计算能够按顺序、不重复地进行，动态规划要求已经求解的子问题不受后续阶段的影响（如果没有先后，谁推导谁就会混乱。这个名词叫做“无后效性”）。

本质上，动态规划对状态空间的遍历，构成了一张有向无环图，遍历顺序就是该有向无环图的一个拓扑序（有向无环图中的node，对应问题中的“状态”。图中的edge对应状态之间的“转移”，转移的选取就是动态规划中的“决策”）。

动态规划用于求最优解的问题时，下一阶段的最优解应该能够由前面各阶段子问题的最优解导出。这个条件被称为”最优子结构性质”（当子结构之间都可以用代表元素和最优解来推导时，称问题满足最优子结构性质）。

在阶段计算完成时，动态规划只会在每个状态上保留与最终解集相关的部分代表信息，这些代表信息应该具有可重复的求解过程，并能够导出后续阶段的代表信息。这样一来，动态规划对状态的抽象和子问题的重叠递进才能够起到优化作用。

1、状态、阶段、决策是构成动态规划算法的三要素
2、子问题重叠性、无后效性、最优子结构是问题能用动态规划求解的三个基本条件

动态规划算法把相同的计算过程作用于各阶段的同类子问题，就好像把一个固定的公式的格式相同的若干输入数据上运行。定义出了动态规划的计算过程，就可以编程实现了，这个计算过程被称为“状态转移方程”。

如何把问题形式化为状态空间，进一步抽象出动态规划的“状态表示”和“阶段划分”，是一件考查智力而非套路的事情。对状态的设计、子结构的挖掘，是核心要点。

Understanding dynamic programming is a milestone in every competitive programmer`s career. While the basic idea is simple, the challenge is how to apply dynamic programming to different problems.

The dynamic programming algorithm is based on a recursive function that goes through all possibilities how to form the sum, like a brute force algorithm.

However, the dynamic programming algorithm is efficient because it uses memoization and calculates the answer to each subproblem only once.

Dynamic Programming is a technique that combines the correctness of complete search and the efficiency of greedy algorithms. Dynamic Programming can be applied if the problem can be divided into overlapping subproblems that can be solved independently. There are two uses for Dynamic Programming:

Finding an optimal solution: We want to find a solution that is as large as possible or as small as possible.
Counting the number of solutions: We want to calculate the total number of possible solutions.

DP问题的描述框架

问题描述
状态表示
阶段划分
转移方程
边界(初始条件)
目标(答案)

具有线性 “阶段” 划分的动态规划算法被称为线性DP，
经典例题：最长上升子序列（LIS）、最长公共子序列（LCS）、数字三角形（IOI1994）

容易发现，无论状态表示是一维还是多维，DP算法在这些问题上都体现为“作用在线性空间上的递推”——DP的阶段沿着各个维度线性增长，从一个或多个“边界点”开始有方向地向整个状态空间转移、扩展。最后，每个状态上都保留了以自身为“目标”的子问题的最优解。

这几个问题也是线性DP中最简单的一类，在这类问题中，需要计算的对象表现出明显的维度以及有序性，每个状态的求解直接构成一个阶段，这使得DP的状态表示就是阶段的表示。

因此，我们只需要在每个维度上各取一个坐标值作为DP的状态，自然就可以描绘出“已求解部分”在状态空间中的轮廓特征，该轮廓的进展就是阶段的推移。

另外，每个状态的求解，显然只与之前阶段的最有解有关，“最优子结构”性质也得以验证。接下来，我们按顺序依次循环每个维度，根据问题要求，递推求解的具体实现过程也就顺理成章了。

下图，形象的描述了线性DP的模样。

LIS问题

递归实现, 以子序列长度作为参数设计函数

// 序列{3, 1, 2, 8, 2, 5, 9}
以 8 为结尾的上升子序列，有
{1, 2, 8}
{3, 8}
{2, 8}
{1, 8}
{8}
在这些子序列中，共同的特点是，结尾都是8
代表元素是 8（注意理解这句话，代表元素是8）
最优解是{1, 2, 8}，长度len = 3

// TLE
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
int a[N], n;
int k[N], ret;                             // 用一个k[N]来存下标，不是直接存具体数值 B[k[N]]
                                           // 而是存有关联的信息，下标
                                           // 这是常见的“简化”
void dfs(int len){                         // 传递的参数len，是最长子序列的长度
    if (len > ret) ret = len;              
    for (int i = k[len] + 1; i <= n; i++)  // 枚举下一个位置是谁
        if (a[i] > a[k[len]]){             // 满足更长一点的条件，就加上
            k[len + 1] = i;
            dfs(len + 1);
        }
}
int main(){
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    k[0] = 0, a[0] = -2e9;
    dfs(0);
    cout << ret << '\n';
    return 0;
}
// 这个搜索，和我们平时的dfs的编写，有些不同
// 平时的dfs，框架是问题的边界，求解子问题
// 这个函数，并没有显性的写出来边界，但是在for循环的时候，如果到了最后一个数，就不会进入for循环
// 也就实现了终止钻下去的过程

#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
int a[N], n;
int ret;                         // 我们发现这个K[]数组是多余，因为每次只用最后一个数
                              // 那么，这最后一个数，就作为函数参数吧
void dfs(int len, int tail){
    if (len > ret) ret = len;
    for (int i = tail + 1; i <= n; i++)
        if (a[i] > a[tail]){
            dfs(len + 1, i);
        }
}
int main(){
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    a[0] = -2e9;
    dfs(0, 0);
    cout << ret << '\n';
    return 0;
}

递归实现, 子集枚举, 选或者不选

int numList[] = {5, 2, 7, 3, 4, 6};    
// solution is finally set of 0s and 1s..pick or leave.
//                 0  1  0  1  1  1
int m = 6;
// called with LIS(0, m)
int LIS(int i, int prev)
{
    if(i == m)
        return 0;
    int choice1 = LIS(i+1, prev);                 // LEAVE
    int choice2 = 0;
    if(prev == m || numList[prev] <= numList[i])
        choice2 = LIS(i+1, i) + 1;
    return max(choice1, choice2);
}
LIS(0, m);  // 需要分析一下，为甚调用的时候prev，传的是m
            // 传-1行不行

循环实现, 刷表法, 填表法

#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
int a[N], n;
int dp[N], ret;
int main(){
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    // 刷表法
    a[0] = -2e9, dp[0] = 0;
    for (int i = 0; i < n; i++)             // 枚举以i为结尾
        for (int j = i + 1; j <= n; j++)    // 枚举下一个数
            if (a[j] > a[i]) dp[j] = max(dp[j], dp[i] + 1); 
    for (int i = 1; i <= n; i++) ret = max(ret, dp[i]);
    cout << ret << '\n';
    return 0;
}

#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
int a[N], n;
int dp[N], ret;
int main(){
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    // 填表法
    a[0] = -2e9, dp[0] = 0;
    for (int i = 1; i <= n; i++)             // 枚举以i为结尾
        for (int j = 0; j < i; j++)          // 枚举从哪个数来
            if (a[j] < a[i]) dp[i] = max(dp[i], dp[j] + 1); 
    for (int i = 1; i <= n; i++) ret = max(ret, dp[i]);
    cout << ret << '\n';
    return 0;
}
// 刷表法，更符合人的正常思考
// 常用的填表法，当前状态，从哪些状态转移过来
// 逆向思维，而已

打印方案

#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
int a[N], n;
int dp[N], ret, tail;
int pre[N];                                    // 记录方案的核心要点是：记录决策
void print(int u){
    if (u == 0) return ;
    print(pre[u]);
    printf("%d ", a[u]);
}
int main(){
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    // 填表法
    a[0] = -2e9, dp[0] = 0;
    for (int i = 1; i <= n; i++)             // 枚举以i为结尾
        for (int j = 0; j < i; j++)          // 枚举从哪个数来
            if (a[j] < a[i]){
                if (dp[i] < dp[j] + 1){
                    dp[i] = dp[j] + 1;
                    pre[i] = j;
                }
            }
    for (int i = 1; i <= n; i++){
        if (ret < dp[i]) ret = dp[i], tail = i;
    }
    cout << ret << '\n';
    print(tail);                             // 找到LIS的最后一个字符，然后开始递归打印方案
    puts("");
    return 0;
}

LCS问题

递归实现

string str1 = "abcdefgzh";
string str2 = "ackghefhlmn";
// abcdefgzh
// 101011001
// ackghefhlmn
// 11000111000
// acefh
// called with LCS(0, 0)
int LCS(int i, int j)
{
    if(i == sz(str1) || j == sz(str2))
        return 0;
    if(str1[i] == str2[j])
        return 1 + LCS(i+1, j+1);
    int choice1 = LCS(i+1, j);
    int choice2 = LCS(i, j+1);
    return max(choice1, choice2);
}

循环实现, O(n^4)

#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
char A[N], B[N];
int n, m, dp[N][N]; // dp[i][j]表示以A[i] B[j]作为结尾的两个子串，最长公共子序列的长度
int main(){
    cin >> n >> m;
    scanf("%s%s", A + 1, B + 1);
    // 这种枚举方式，是知道具体公共的位置，O(n^4) ，超时
    // 同时，我们也并不需要知道具体是哪个位置公共的
    for (int i = 0; i < n; i++)          // 枚举A取到了i位置, B取到了j位置
        for (int j = 0; j < m; j++){     
            if (A[i] != B[j]) continue;  // 当A[i] == B[j]，就符合公共条件，可以看下一个位置
            for (int ni = i + 1; ni <= n; ni++)  // 两重循环枚举下一个可能位置是什么
                for (int nj = j + 1; nj <= m; nj++)
                    if (A[ni] == B[nj]) dp[ni][nj] = max(dp[ni][nj], dp[i][j] + 1);
        }
    int ret = 0;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            ret = max(ret, dp[i][j]);
    cout << ret << '\n';
    return 0;
}

循环实现, O(n^2)

#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
char A[N], B[N];
int n, m, dp[N][N]; // dp[i][j]表示以A[i] B[j]作为结尾的两个子串，最长公共子序列的长度
int main(){
    cin >> n >> m;
    scanf("%s%s", A + 1, B + 1);
    for (int i = 1; i <= n; i++) dp[i][0] = 0;  // B串0个字符，公共长度就是0
    for (int j = 1; j <= m; j++) dp[0][j] = 0;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++){
            // dp[i-1][j] 以A[i-1] B[j]为结尾的两个子串，最长公共子序列长度
            // dp[i][j-1] 以A[i] B[j-1]为结尾的两个子串，最长公共子序列长度
            // 并不需要子序列的结尾就是i，或者就是j
            dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]); 
            if (A[i] == B[j]) dp[i][j] = max(dp[i][j], dp[i - 1][j - 1] + 1);
        }
    cout << dp[n][m] << '\n';
    return 0;
}

打印方案

// 打印方案
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
char A[N], B[N];
int n, m, dp[N][N]; // dp[i][j]表示以A[i] B[j]作为结尾的两个子串，最长公共子序列的长度
int pre[N][N];      // 核心：记录如何转移的, 记决策
void print(int i, int j){
    if (i == 0 || j == 0) return ;
    if (pre[i][j] == 3){
        print(i - 1, j - 1);
        printf("%c", A[i]);
    }
    else if (pre[i][j] == 1) print(i - 1, j);
    else if (pre[i][j] == 2) print(i, j - 1);
}
int main(){
    cin >> n >> m;
    scanf("%s%s", A + 1, B + 1);
    for (int i = 1; i <= n; i++) dp[i][0] = 0;  // B串0个字符，公共长度就是0
    for (int j = 1; j <= m; j++) dp[0][j] = 0;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++){
            if (dp[i - 1][j] > dp[i][j - 1]){
                dp[i][j] = dp[i - 1][j];
                pre[i][j] = 1;
            }
            else{
                dp[i][j] = dp[i][j - 1];
                pre[i][j] = 2;
            }
            if (A[i] == B[j]){
                if (dp[i - 1][j - 1] + 1 > dp[i][j]){
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                    pre[i][j] = 3;
                }
            } 
        }
    cout << dp[n][m] << '\n';
    print(n, m);
    puts("");
    return 0;
}

数字三角形问题

递归实现, TLE

#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int a[N][N], dp[N][N], f[N][N];
int n;
int solve(int x, int y)
{
    // 问题的边界
    if (x == n) return a[x][y];
    // 求解子问题
    int u = solve(x + 1, y);
    int v = solve(x + 1, y + 1);
    if (u > v) return a[x][y] + u;
    else return a[x][y] + v;
}
int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++){
        for (int j = 1; j <= i; j++)
            cin >> a[i][j];
    }
    cout << solve(1, 1) << '\n';
    return 0;
}

递归实现, 记忆化

#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int mem[N][N];
int a[N][N], dp[N][N], f[N][N];
int n;
int solve(int x, int y)
{
    //问题的边界
    if (x == n) return a[x][y];
    int &ret = mem[x][y];
    if (ret != -1) return ret;
    //求解子问题
    int u = solve(x + 1, y);
    int v = solve(x + 1, y + 1);
    if (u > v) return ret = a[x][y] + u;
    else return ret = a[x][y] + v;
}
int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++){
        for (int j = 1; j <= i; j++)
            cin >> a[i][j];
    }
    //递归+记忆化
    memset(mem, -1, sizeof mem);
    cout << solve(1, 1) << '\n';
    return 0;
}

循环实现, 从上往下

#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int mem[N][N];
int a[N][N], dp[N][N], f[N][N];
int n;
void recur01()
{
    dp[1][1] = a[1][1];
    for (int i = 2; i <= n; i++)
        for (int j = 1; j <= i; j++)
            dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - 1]) + a[i][j];
    int maxn = -2e9;
    for (int j = 1; j <= n; j++)
        maxn = max(maxn, dp[n][j]);
    cout << maxn << '\n';
}
int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++){
        for (int j = 1; j <= i; j++)
            cin >> a[i][j];
    }
       recur01();
    return 0;
}

循环实现, 从下往上

#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int mem[N][N];
int a[N][N], dp[N][N], f[N][N];
int n;
void recur02()
{
    for (int j = 1; j <= n; j++) f[n][j] = a[n][j];
    for (int i = n - 1; i >= 1; i--)
        for (int j = i; j >= 1; j--){
            f[i][j] = a[i][j] + max(f[i+1][j], f[i+1][j+1]);
        }
    cout << f[1][1] << '\n';
}
int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++){
        for (int j = 1; j <= i; j++)
            cin >> a[i][j];
    }
    recur02();
    return 0;
}

例题：898. 数字三角形

acwing上的数据更丰富一些，需要对dp进行初始化成负无穷，每一行0 ~ i+1都要初始化

01背包问题(Subset Sum)

递归实现

// 题面：W代表重量，P代表价值
// W: 10, 4 , 20, 5, 7
// P: 10, 15, 3 , 1, 4
// knapsack size = 12
//      0   1   0   0  1
const int MAX = 5;
int n = 5;
int weights[MAX] = {10, 4, 20, 5, 7};
int benfit[MAX] = {10, 15, 3, 1, 4};
int knapsack(int i, int reminder)    // aka 0/1 knapsack
{
    if(i == n)
        return 0;
    int choice1 = knapsack(i+1, reminder);
    int choice2 = 0;
    if(reminder >= weights[i])
        choice2 = knapsack(i+1, reminder - weights[i]) + benfit[i];
    return max(choice1, choice2);
}
// called with knapsack(0, intialWeight)

循环实现, 求解最大值/最小值

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];
    for (int i = 1; i <= n; i++)
        for (int j = 0; j <= m; j++)
        {
            f[i][j] = f[i - 1][j];              // 右边集合为空，不包含i
            if (j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
        }
    cout << f[n][m] << endl;
    return 0;
}

循环实现, 剩余最小空间, 求解最大值最小值(提供了多种代码)

例题，1295：装箱问题

【描述】
有一个箱子容量为 V(正整数，0 ≤ v ≤ 20000)，同时有n个物品(0< n ≤30)，
每个物品有一个体积(正整数）。
求n个物品中，任取若干个装入箱内，使箱子的剩余空间为最小。
【输入】
第一行是一个整数V，表示箱子容量。
第二行是一个整数n，表示物品数。
接下来n行，每行一个正整数（不超过10000），分别表示这n个物品的各自体积。
【输出】
一个整数，表示箱子剩余空间。
【输入样例】
24
6
8
3
12
7
9
7
【输出样例】
0

// 递归实现，时间复杂度O(2^n)
// dfs(u, m)表示当前第u个物品，总共占用m体积，返回的是实际使用的体积
// called with dfs(1, 0)
#include <bits/stdc++.h>
using namespace std;
const int N = 20010, M = 35;
int w[M];
int n, V;
int dfs(int u, int m){
    if (u > n) return 0;
    int c1 = 0, c2 = 0;
    c1 = dfs(u + 1, m);
    if (m + w[u] <= V) c2 = dfs(u + 1, m + w[u]) + w[u];
    return max(c1, c2);
}
int main()
{
    cin >> V >> n;
    for (int i = 1; i <= n; i++) cin >> w[i];
    cout << V - dfs(1, 0) << '\n';
    return 0;
}
// 这个方法应该是不能过的，但是题目的数据比较小，还是过了

// 还是递归实现，遍历的顺序发生调整，从大到小
// 主函数调用dfs(n, v)
#include <bits/stdc++.h>
using namespace std;
const int N = 20010, M = 35;
int w[M];
int n, V;
int dfs(int u, int m){
    if (u == 0) return 0;
    int c1 = 0, c2 = 0;
    c1 = dfs(u - 1, m);
    if (m >= w[u]) c2 = dfs(u - 1, m - w[u]) + w[u];
    return max(c1, c2);
}
int main()
{
    cin >> V >> n;
    for (int i = 1; i <= n; i++) cin >> w[i];
    cout << V - dfs(n, V) << '\n';
    return 0;
}
// 上面两个程序的本质是一样的，为了熟练使用搜索，这些是很好的练习角度
// 更好的是，在这种方法上，加上记忆化，基本是万能流

// 加上记忆化，执行时间在ybt平台上，最后一个测试点是33ms,降到了3ms（似乎比循环还要快一点）
#include <bits/stdc++.h>
using namespace std;
const int N = 20010, M = 35;
int w[M], mem[M][N];
int n, V;
int dfs(int u, int m){
    if (u == 0) return 0;
    int &ret = mem[u][m];
    if (ret != -1) return ret;
    int c1 = -1, c2 = -1;
    c1 = dfs(u - 1, m);
    if (m >= w[u]) c2 = dfs(u - 1, m - w[u]) + w[u];
    return ret = max(c1, c2);
}
int main()
{
    cin >> V >> n;
    for (int i = 1; i <= n; i++) cin >> w[i];
    memset(mem, -1, sizeof mem);
    cout << V - dfs(n, V) << '\n';
    return 0;
}

// 循环实现
// 时间复杂度O(n^2)，空间复杂度O(n^2)
#include <bits/stdc++.h>
using namespace std;
const int N = 20010, M = 35;
int dp[M][N], w[M];   // dp[i][j]表示前i个物品使用空间j的情况下，实际放了多少体积的东西 
int n, V;
int main()
{
    cin >> V >> n;
    for (int i = 1; i <= n; i++) cin >> w[i];
    for (int i = 1; i <= n; i++)
        for (int j = 0; j <= V; j++){
            dp[i][j] = max(dp[i][j], dp[i - 1][j]);
            if (j >= w[i]) dp[i][j] = max(dp[i][j], dp[i - 1][j - w[i]] + w[i]);
        }
    cout << V - dp[n][V] << '\n';
    return 0;
}

// 循环时间，优化空间复杂度
// 时间复杂度O(n^2)，空间复杂度O(n)
#include <bits/stdc++.h>
using namespace std;
const int N = 20010, M = 35;
int dp[N], w[M];
int n, V;
int main()
{
    cin >> V >> n;
    for (int i = 1; i <= n; i++) cin >> w[i];
    for (int i = 1; i <= n; i++)
        for (int j = V; j >= w[i]; j--)
            dp[j] = max(dp[j], dp[j - w[i]] + w[i]);
    cout << V - dp[V] << '\n';
    return 0;
}

// 总结
// 这道题目，我们用了多种方法，把一个简单问题复杂化
// 通过简单问题的简单背景，弱化非主要目标，集中注意力到问题的本质
// 复杂化，多种角度的解决本质问题，从而提高对本质的理解
// 日后实际工作中，遇到的问题，基本都是复杂的问题，但拨开非主要目标
// 暴露出来的核心问题，就是本质，就是我们很熟悉的本质
// 然后，就可以多角度，随心所欲的搞
// 其中，拨开非主要目标的这个过程，往往需要较好的阅读理解能力

循环实现, 求解可行性

// 时间复杂度O(n^2)，空间复杂度O(n^2)
possible[0][0] = true;
for (int k = 1; k <= n; k++) {
    for (int x = 0; x <= W; x++) {
       if (x-w[k] >= 0) possible[x][k] |= possible[x-w[k]][k-1];
       possible[x][k] |= possible[x][k-1];
    } 
}
// 时间复杂度O(n^2)，空间复杂度O(n)
// trick是枚举x的时候，从大往小枚举
possible[0] = true;
for (int k = 1; k <= n; k++) {
    for (int x = W; x >= 0; x--) {
       if (possible[x]) possible[x+w[k]] = true;
    } 
}

edit distance编辑距离

aka, Levenshtein distance莱文斯坦距离(aka, also known as)

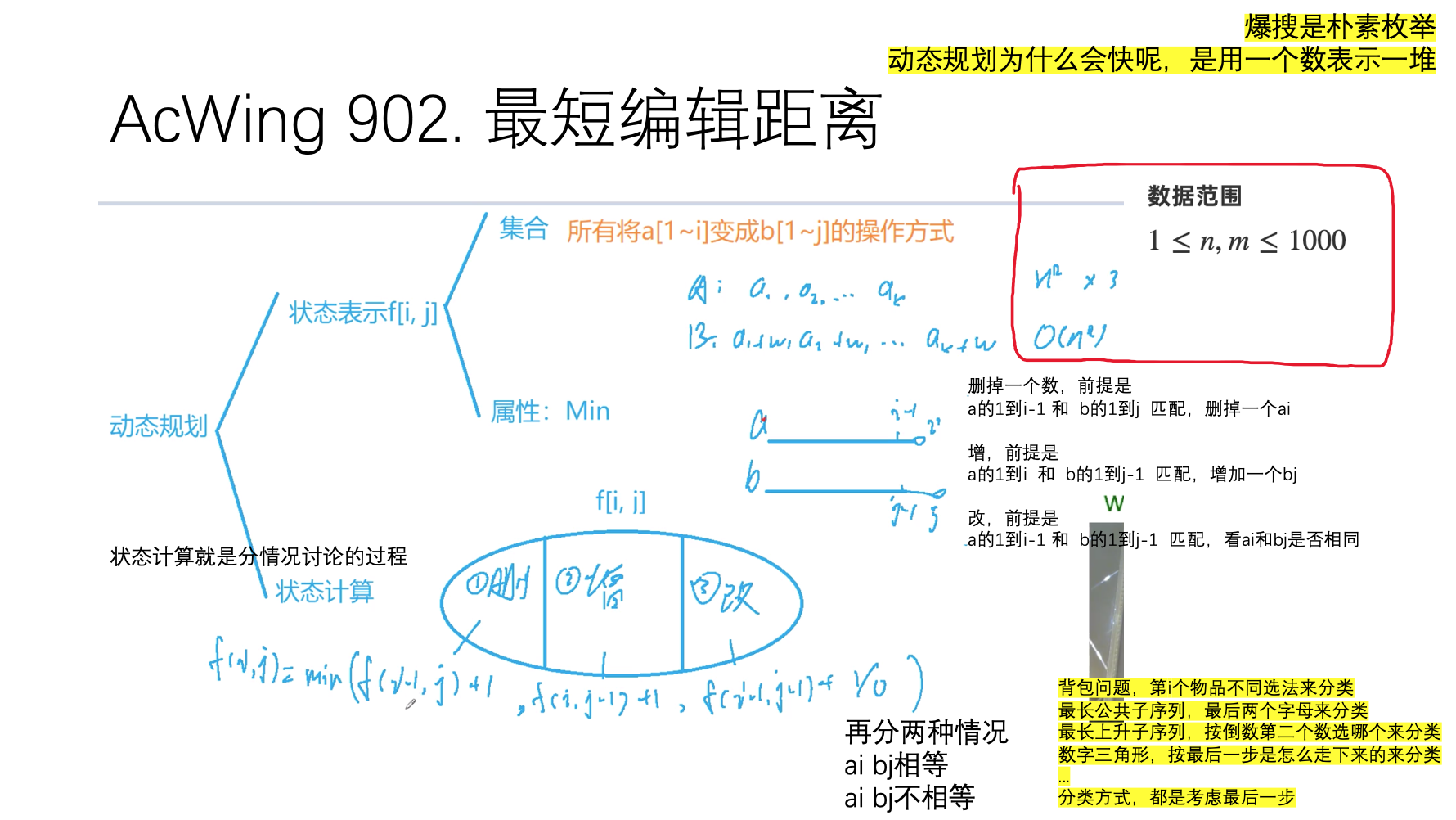
字符串A("xyzab")和字符串B("axyzc")，问至少经过多少步操作可以把A变成B。
我们还是从两个字符串的最后一个字符来考察即'b'和'c'。显然二者不相同，那么我们有以下三种处理办法：
(1)增加：在A末尾增加一个'c'，那么A变成了"xyzabc"，B仍然是"axyzc"，由于此时末尾字符相同了，那么就变成了比较"xyzab"和"axyz"的距离，即d(xyzab,axyzc) = d(xyzab,axyz) + 1
可以写成d(i,j) = d(i,j-1) + 1。表示下次比较的字符串B的长度减少了1，而加1表示当前进行了一次字符的操作
(2)删除：删除A末尾的字符'b'，考察A剩下的部分与B的距离。即d(xyzab,axyzc) = d(xyza,axyzc) + 1
可以写成d(i,j) = d(i-1,j) + 1。表示下次比较的字符串A的长度减少了1
(3)替换：把A末尾的字符替换成'c'，这样就与B的末尾字符一样了，那么接下来就要考察出了末尾'c'部分的字符，即d(xyzab,axyzc) = d(xyza,axyz) + 1
写成d(i,j) = d(i-1,j-1) + 1表示字符串A和B的长度均减少了1
参考：https://www.jianshu.com/p/12e9b9a9a350

例题，【例9.20】编辑距离

// 示例代码
// 编辑距离的问题，和LCS很像很像
// 放在一块进行对比学习，更有帮助
#include <bits/stdc++.h>
using namespace std;
const int N = 2010;
char a[N], b[N];
int n, m;
int dp[N][N];
int main()
{
    scanf("%s%s", a + 1, b + 1);
    n = strlen(a + 1), m = strlen(b + 1);
    dp[0][0] = 0;
    for (int i = 1; i <= n; i++) dp[i][0] = i;
    for (int j = 1; j <= m; j++) dp[0][j] = j;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++){
            dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + 1; 
            if (a[i] == b[j]) dp[i][j] = min(dp[i][j], dp[i-1][j-1]);
            else dp[i][j] = min(dp[i][j], dp[i-1][j-1] + 1);
        }
    cout << dp[n][m] << '\n';
    return 0;
}

信息学奥赛21天突破

动态规划第2讲进阶指南

动态规划相关术语《进阶指南》

DP问题的描述框架

LIS问题

递归实现, 以子序列长度作为参数设计函数

递归实现, 子集枚举, 选或者不选

循环实现, 刷表法, 填表法

打印方案

LCS问题

递归实现

循环实现, O(n^4)

循环实现, O(n^2)

打印方案

数字三角形问题

递归实现, TLE

递归实现, 记忆化

循环实现, 从上往下

循环实现, 从下往上

例题：898. 数字三角形

01背包问题(Subset Sum)

递归实现

循环实现, 求解最大值/最小值

循环实现, 剩余最小空间, 求解最大值最小值(提供了多种代码)

例题，1295：装箱问题

循环实现, 求解可行性

edit distance编辑距离

例题，【例9.20】编辑距离

动态规划 第2讲 进阶指南

动态规划相关术语《进阶指南》

DP问题的描述框架

LIS问题

递归实现, 以子序列长度作为参数设计函数

递归实现, 子集枚举, 选或者不选

循环实现, 刷表法, 填表法

打印方案

LCS问题

递归实现

循环实现, O(n^4)

循环实现, O(n^2)

打印方案

数字三角形问题

递归实现, TLE

递归实现, 记忆化

循环实现, 从上往下

循环实现, 从下往上

例题：898. 数字三角形

01背包问题(Subset Sum)

递归实现

循环实现, 求解最大值/最小值

循环实现, 剩余最小空间, 求解最大值最小值(提供了多种代码)

例题，1295：装箱问题

循环实现, 求解可行性

edit distance编辑距离

例题，【例9.20】编辑距离

动态规划第2讲进阶指南