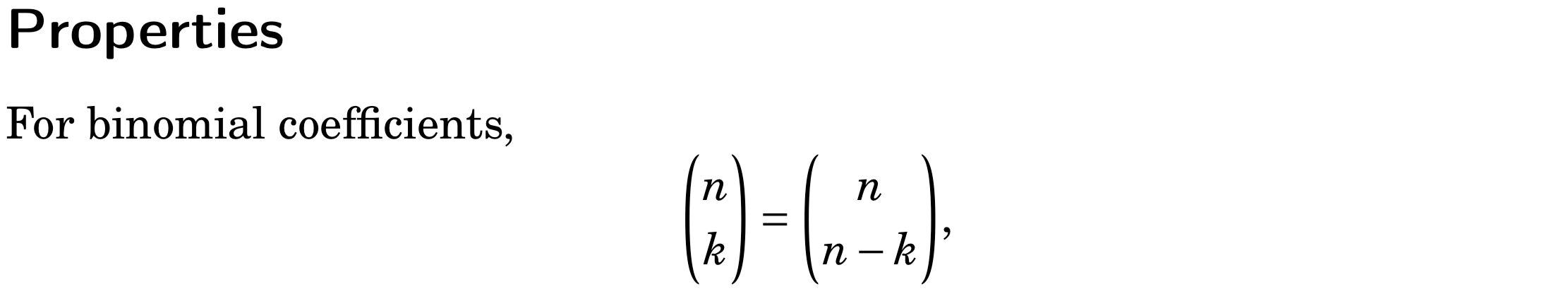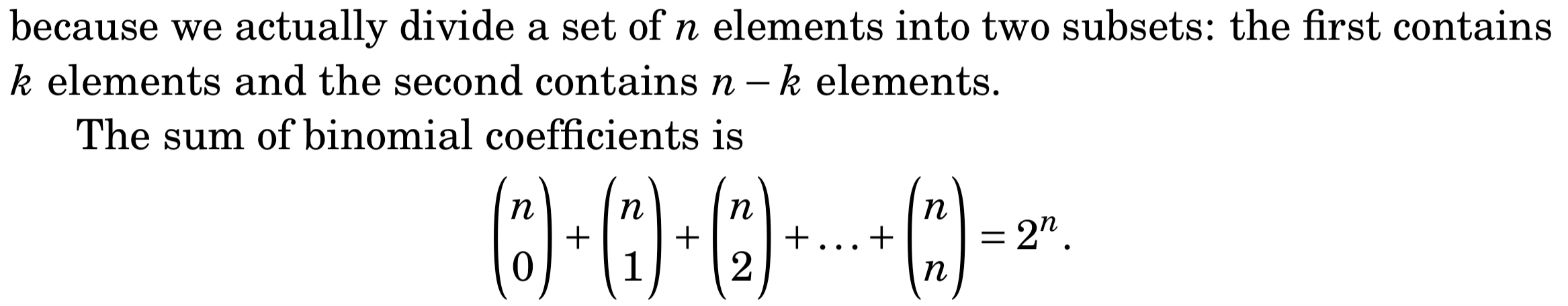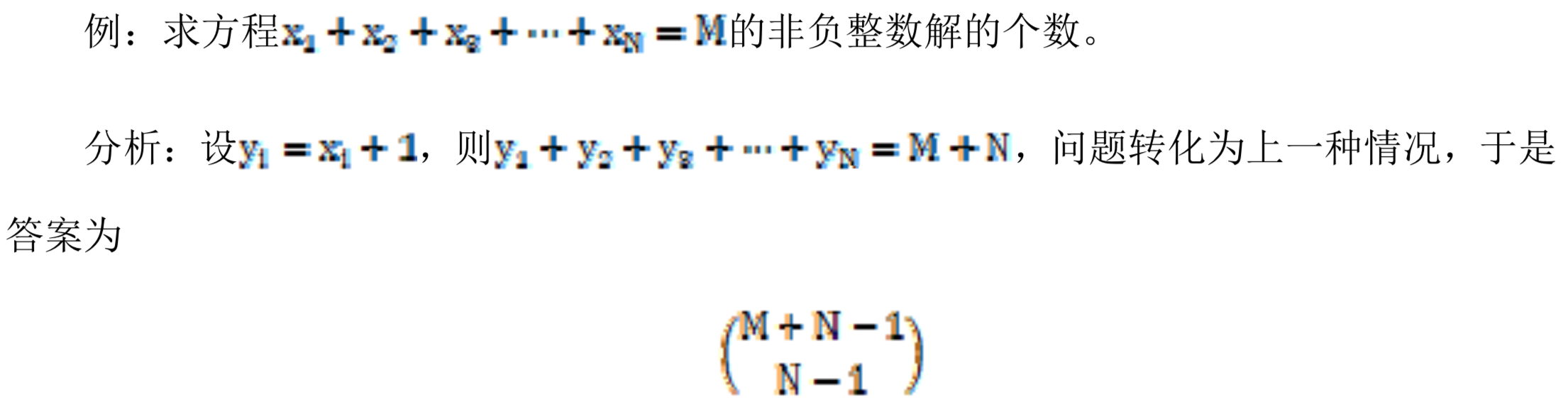- Primes and factors素数和因子
- Number of primes
- 试除法判断素数
- 分解质因子
- 朴素筛法O(nlogn)
- 埃式筛法O(n) O(nloglogn)
- 线性筛 O(n)
- 约数个数
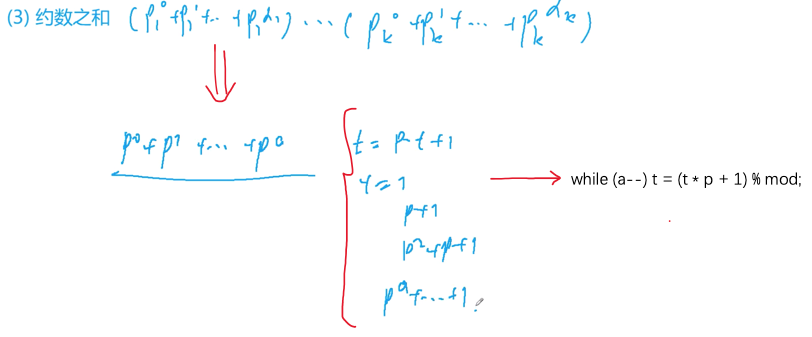
- 约数之和
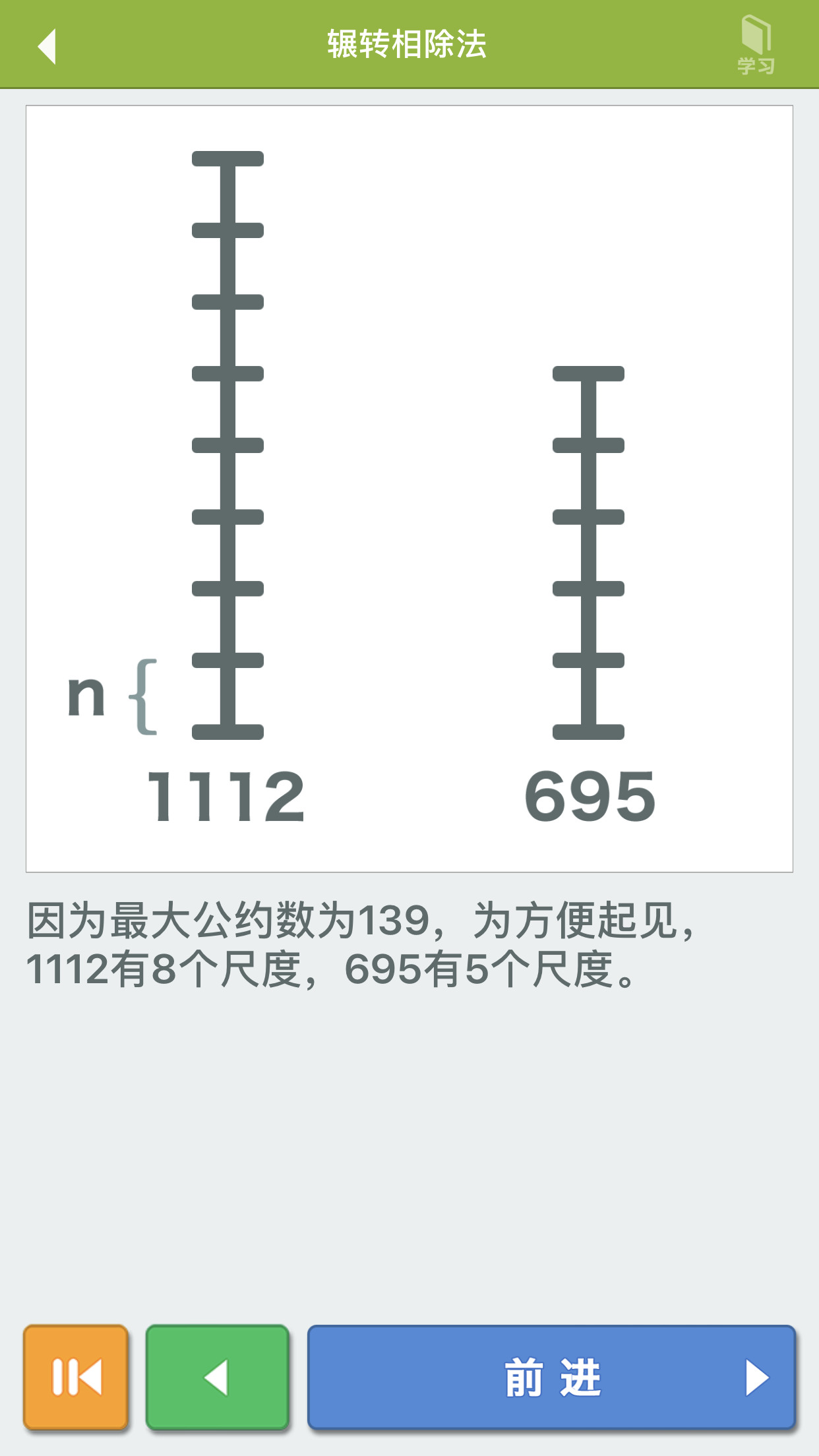
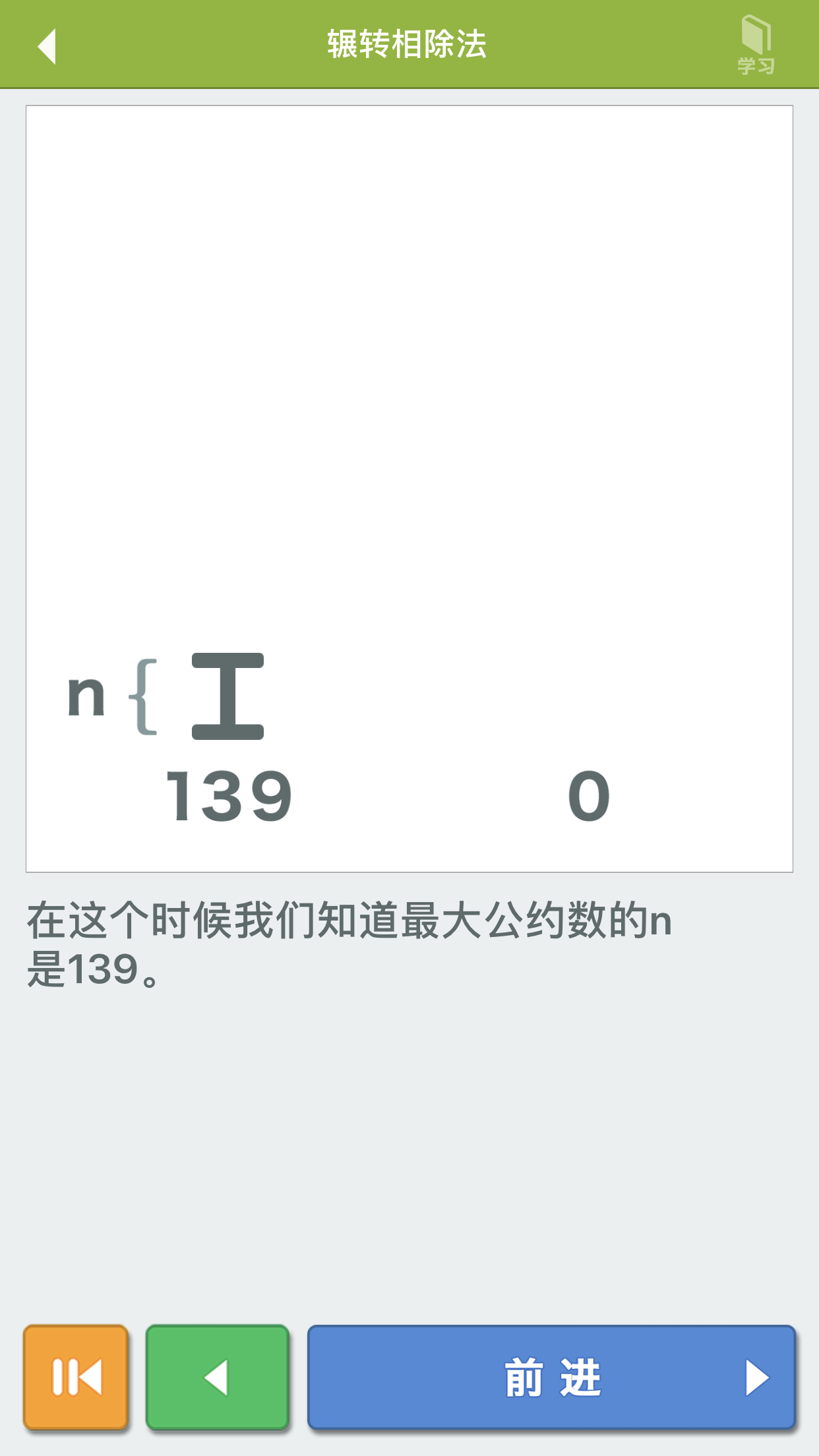
- 欧几里得算法(最大公约数)
- 欧拉函数
- 筛法求欧拉函数
- 快速幂
- Modular arithmetic模运算
- Fermat’s theorem费马定理
- Fermat’s Last Theorem费马大定理
- Fermat’s little theorem费马小定理
- Euler’s theorem欧拉定理
- Derangements错位排列
- 加法原理和乘法原理
- 排列和排列数
- 组合和组合数
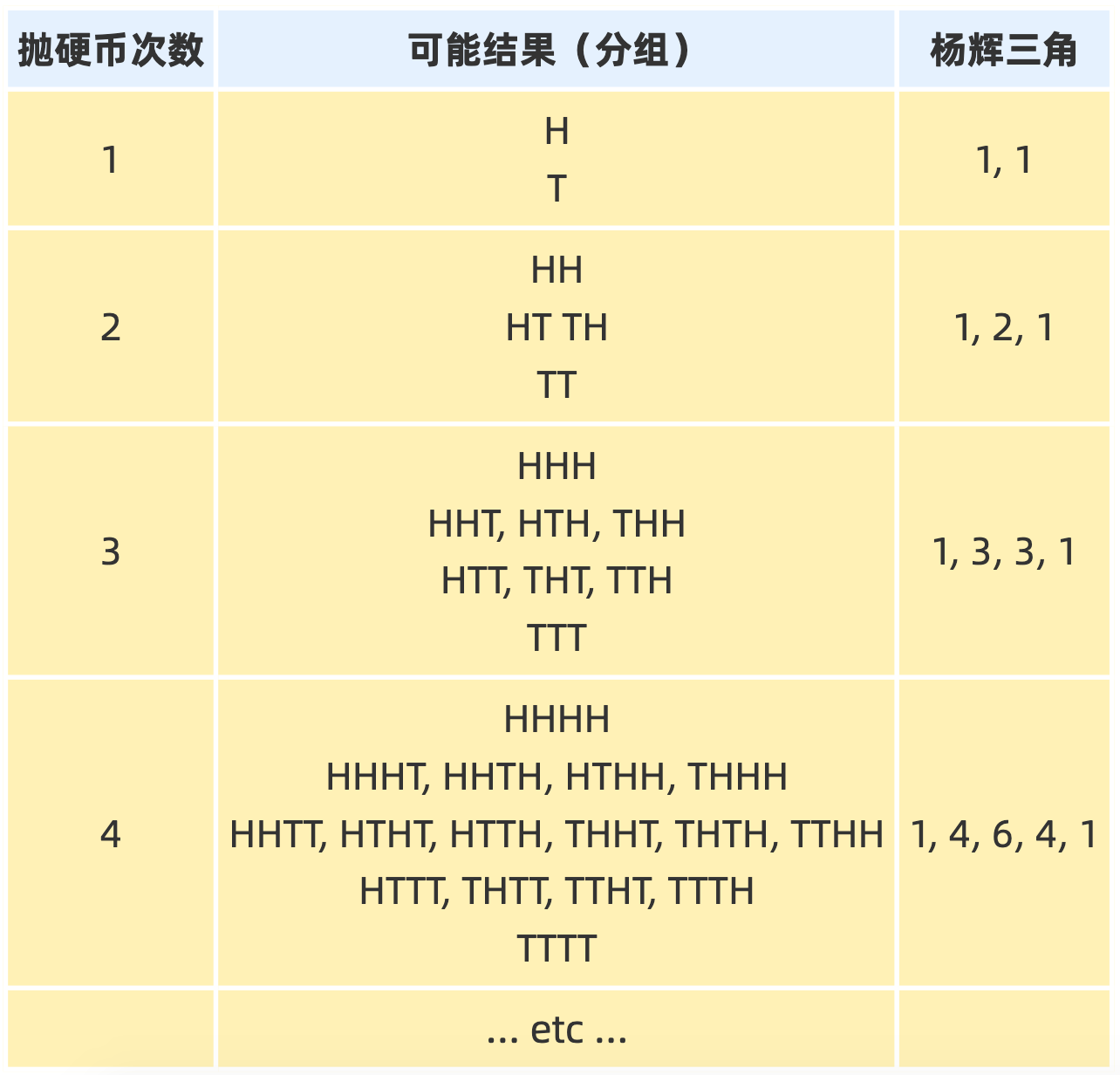
- 杨辉三角Pascal`s triangle
- 常见计数方法
- 容斥原理
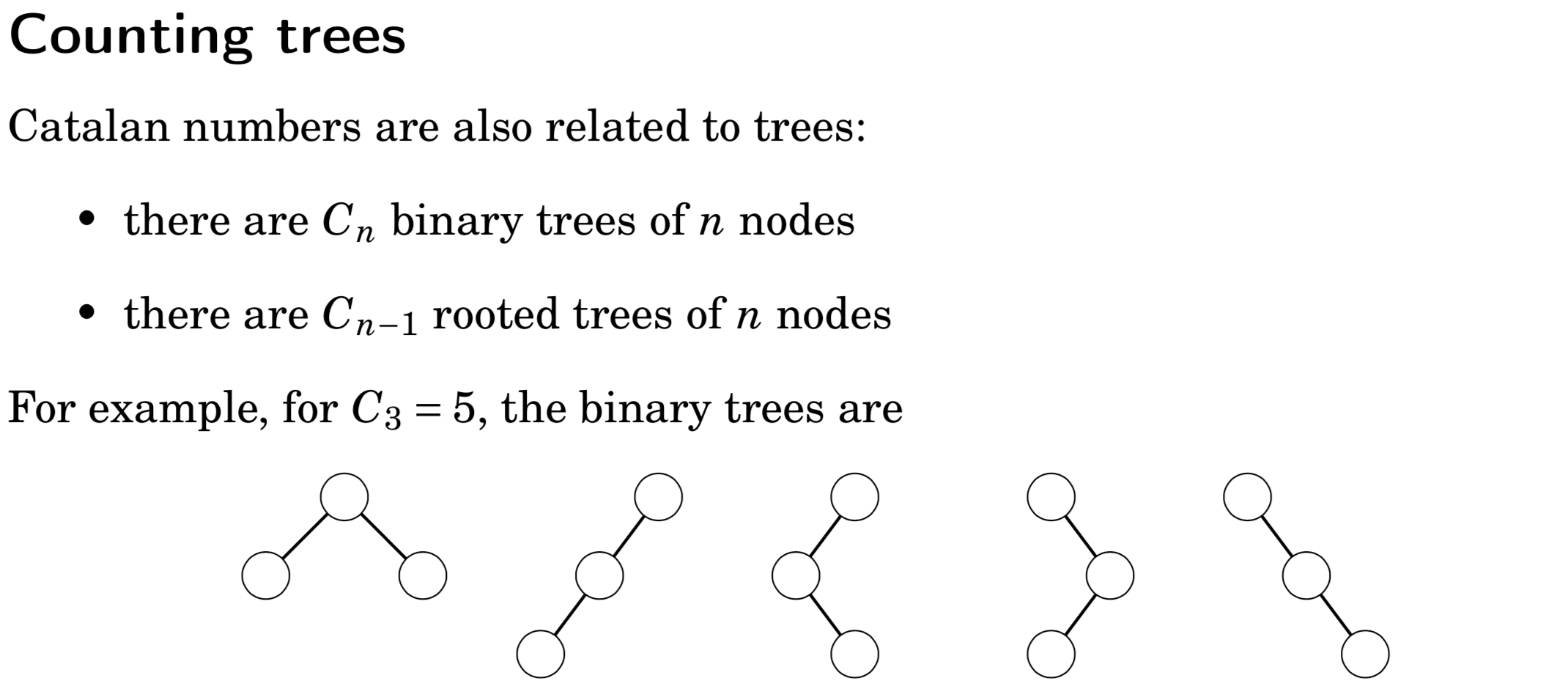
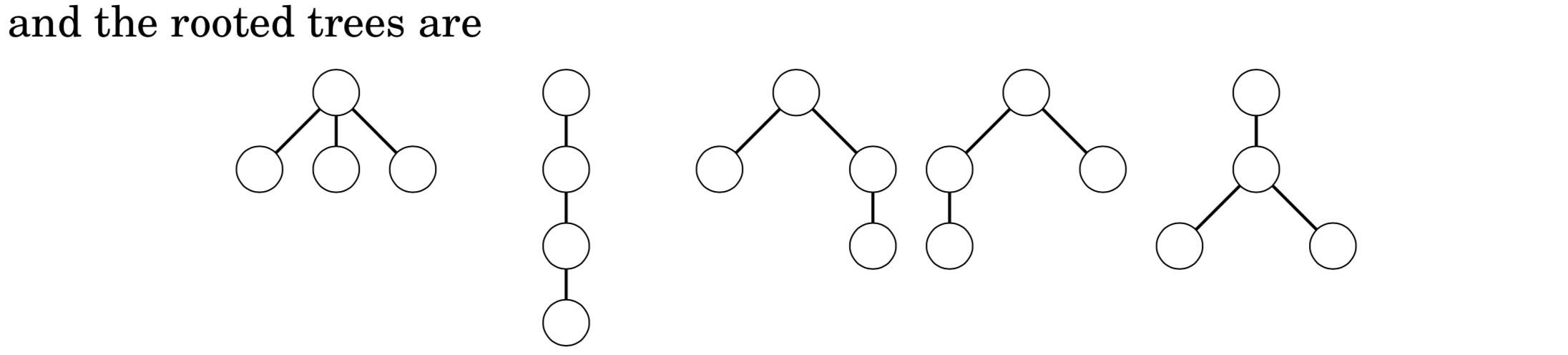
- Catalan numbers卡特兰数
- 杨辉三角
- 杨辉三角的应用
- 插板法原理及应用

Primes and factors素数和因子

Number of primes

One interesting class of prime: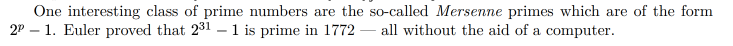
试除法判断素数
bool is_prime(int x){if (x < 2) return false;for (int i = 2; i <= x / i; i++)if (x %i == 0) return false;return true;}
分解质因子
void divide(int x){for (int i = 2; i <= x / i; i++)if (x % i == 0){int s = 0; // 计数器,记录个数while (x % i == 0) x /= i, s++;cout << i << ' ' << s << endl;}if (x > 1) cout << x << ' ' << 1 << endl;puts("");}
朴素筛法O(nlogn)
void get_primes(int n){for (int i = 2; i <= n; i++){if (!st[i]){primes[cnt++] = i;}for (int j = i + i; j <= n; j += i) st[j] = true;}}

埃式筛法O(n) O(nloglogn)
void get_primes(int n){for (int i = 2; i <= n; i++){if (st[i]) continue;primes[cnt++] = i;for (int j = i + i; j <= n; j += i)st[j] = true;}}

线性筛 O(n)
// 核心:n只会被他的最小质因子筛掉void get_primes(int n){for (int i = 2; i <= n; i++){if (!st[i]) primes[cnt++] = i;for (int j = 0; primes[j] <= n / i; j++){st[primes[j] * i] = true;if (i % primes[j] == 0) break;}}}
约数个数
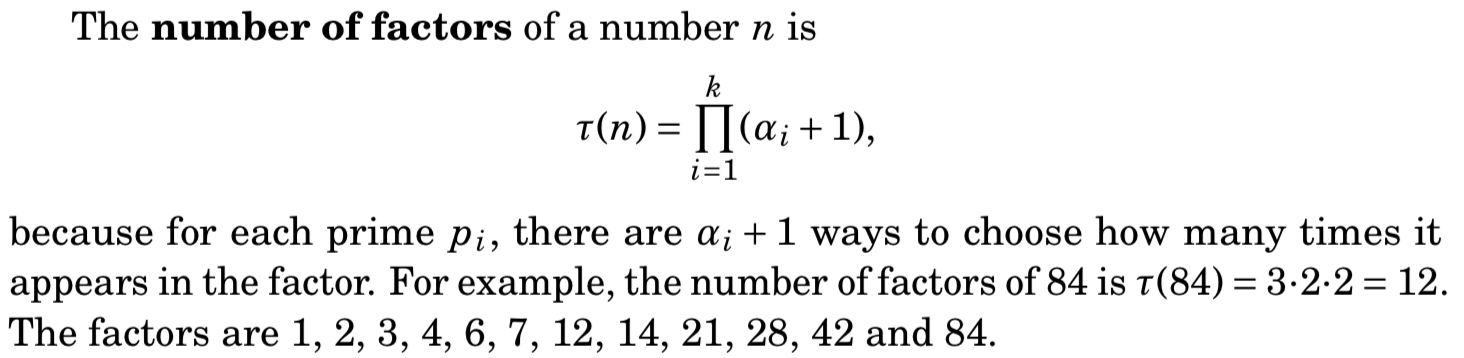
#include <iostream>#include <unordered_map>using namespace std;typedef long long LL;const int mod = 1e9 + 7;int main(){int n;cin >> n;unordered_map<int, int> primes;while (n--){int x;cin >> x;for (int i = 2; i <= x / i; i++)while (x % i == 0){x /= i;primes[i] ++;}if (x > 1) primes[x]++;}LL res = 1;unordered_map<int, int>::iterator it;for (it = primes.begin(); it != primes.end(); it++)res = res * ((*it).second + 1) % mod;cout << res << endl;return 0;}
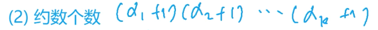
约数之和
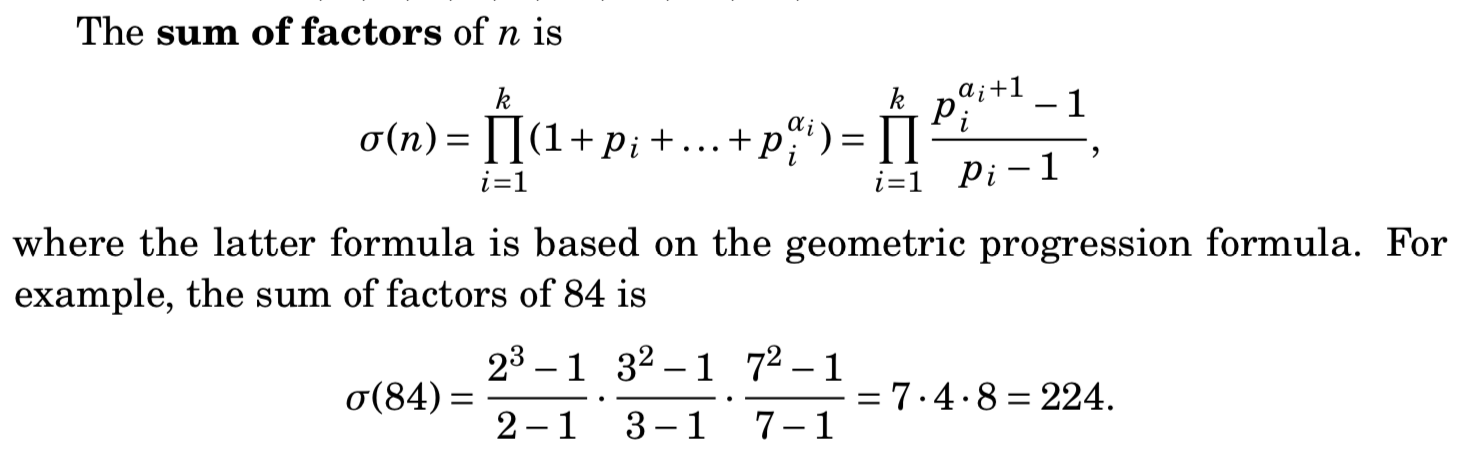
#include <iostream>#include <algorithm>#include <unordered_map>using namespace std;typedef long long LL;const int mod = 1e9 + 7;int main(){int n;cin >> n;unordered_map<int, int> primes;while (n--){int x;cin >> x;for (int i = 2; i <= x / i; i++)while (x % i == 0){x /= i;primes[i]++;}if (x > 1) primes[x]++;}LL res = 1;for (auto prime : primes){int p = prime.first, a = prime.second;LL t = 1;while (a--) t = (t * p + 1) % mod;res = res * t % mod;}cout << res << endl;return 0;}
欧几里得算法(最大公约数)
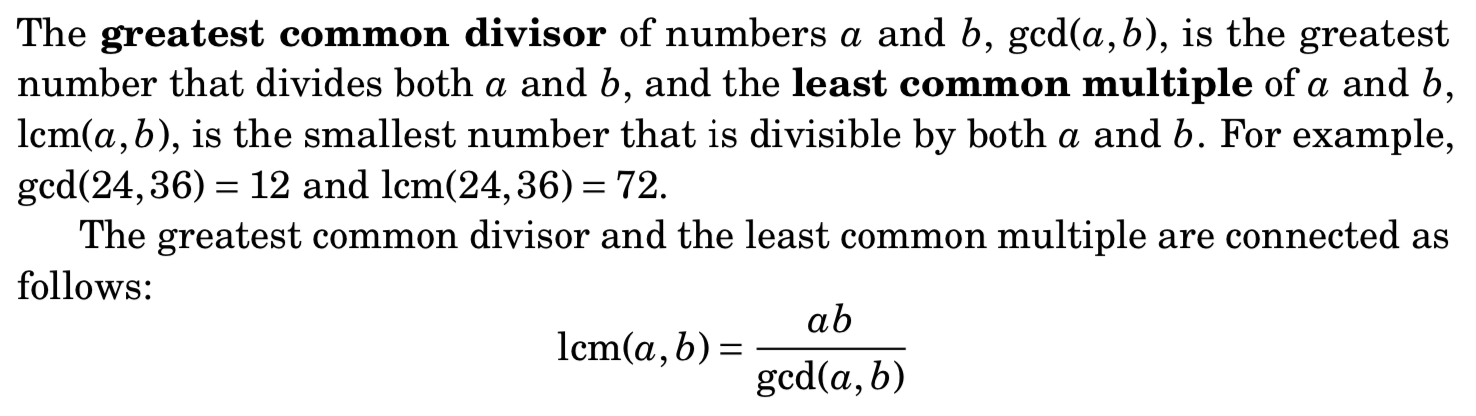

int gcd(int a, int b) {if (b == 0)return a;return gcd(b, a % b);}int gcd(int a, int b){return b ? gcd(b, a % b) : a;}int gcd(int a, int b) {int tmp;while(b != 0) {tmp = b;b = a % b;a = tmp;}return a;}


欧拉函数

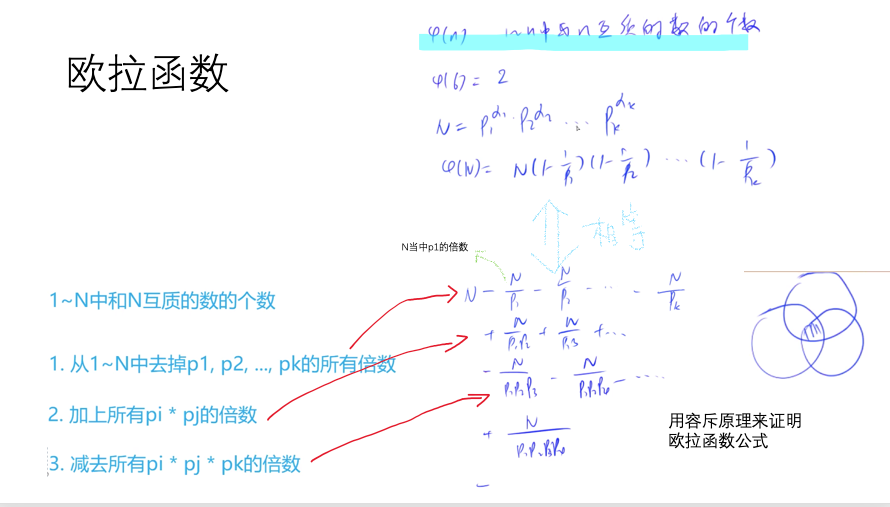
#include <iostream>#include <algorithm>using namespace std;int main(){int n;cin >> n;while (n--){int a;cin >> a;int res = a;for (int i = 2; i <= a / i; i++){if (a % i == 0){//res = res * (1 - 1 / i); //整除的问题,要调整一下res = res / i * (i - 1);while (a % i == 0) a /= i;}}if (a > 1) res = res / a * (a - 1);cout << res << endl;}return 0;}
筛法求欧拉函数
快速幂
// 返回a^k % pint qmi(int a, int k, int p){int res = 1;while (k) //当k不是0的时候{if (k & 1) res = (LL)res * a % p;k >>= 1;a = (LL)a * a % p;}return res;}
Modular arithmetic模运算

核心:随时取模
Fermat’s theorem费马定理
https://en.wikipedia.org/wiki/Fermat%27s_theorem
The works of the 17th-century mathematician Pierre de Fermat engendered many theorems. Fermat’s theorem may refer to one of the following theorems:
- Fermat’s Last Theorem, about integer solutions to an + bn = cn
- Fermat’s little theorem, a property of prime numbers
- Fermat’s theorem on sums of two squares, about primes expressible as a sum of squares
- Fermat’s theorem (stationary points)), about local maxima and minima of differentiable functions
- Fermat’s principle, about the path taken by a ray of light
- Fermat polygonal number theorem, about expressing integers as a sum of polygonal numbers
- Fermat’s right triangle theorem, about squares not being expressible as the difference of two fourth powers
Fermat’s Last Theorem费马大定理
https://en.wikipedia.org/wiki/Fermat%27s_Last_Theorem

Fermat’s little theorem费马小定理
https://en.wikipedia.org/wiki/Fermat%27s_little_theorem
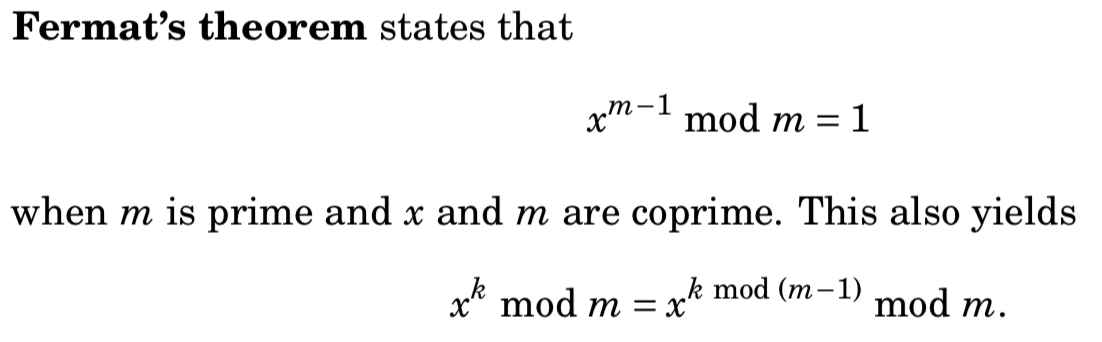
Euler’s theorem欧拉定理
Derangements错位排列

https://blog.csdn.net/bengshakalakaka/article/details/83420150
加法原理和乘法原理

排列和排列数
组合和组合数
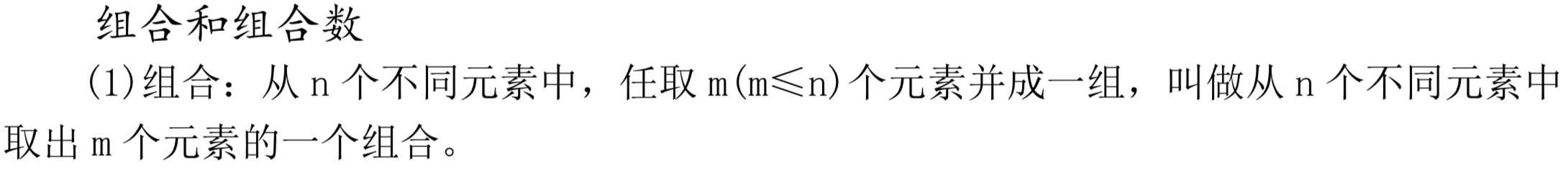

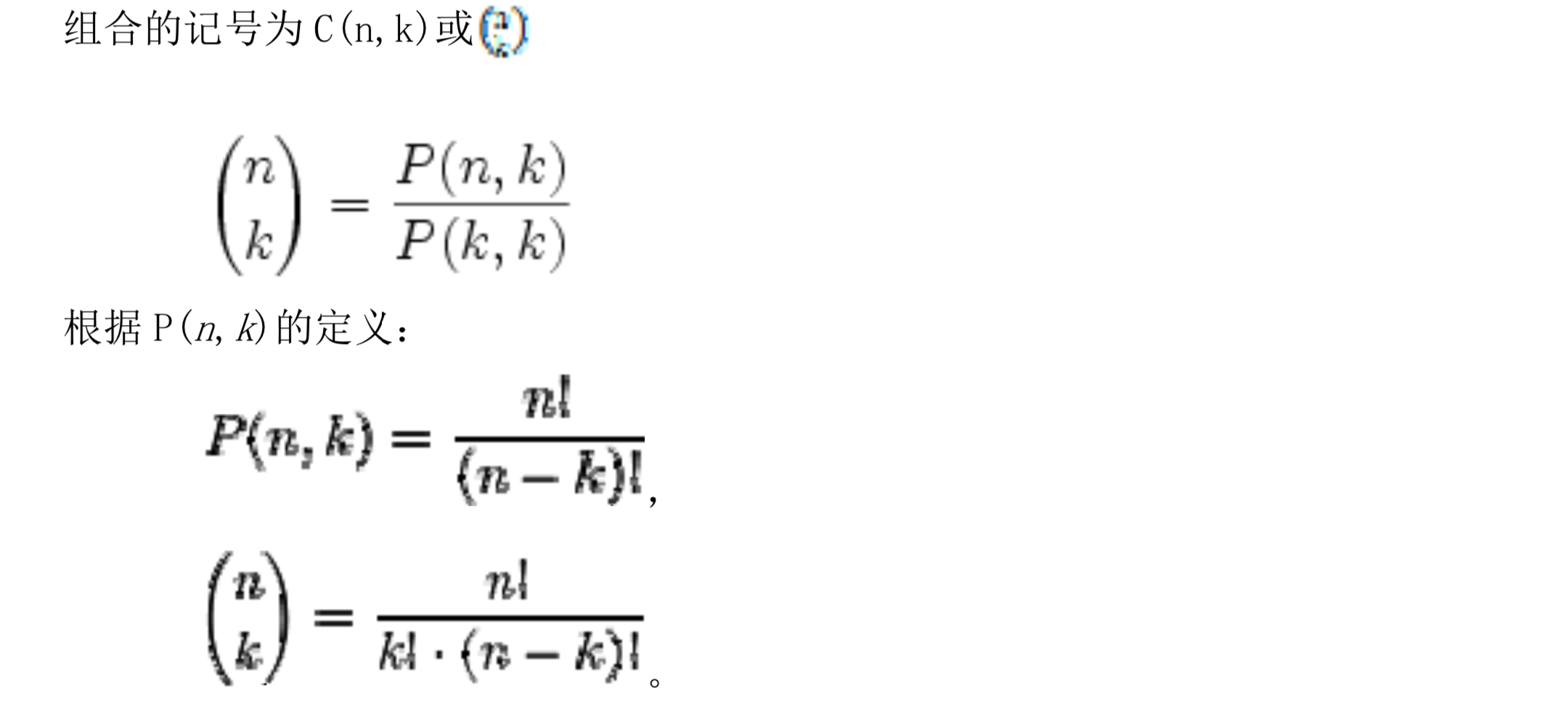
更多的查看:https://oi-wiki.org/math/combinatorics/combination/
示例代码
#include <bits/stdc++.h>using namespace std;typedef long long ll;int n, m;ll C(int n, int m){ll sum = 1ll;for (int i = 1; i <= m; i++)sum = sum * (n - m + i) / i;return sum;}int main(){cin >> n >> m;cout << C(n, m) << '\n';return 0;}
#include <bits/stdc++.h>using namespace std;typedef long long ll;const int N = 110;int n, m;ll C[N][N];int main(){cin >> n >> m;C[0][0] = 1;for (int i = 1; i <= n; i++){C[i][0] = C[i][i] = 1;for (int j = 1; j <= n; j++) C[i][j] = C[i - 1][j] + C[i - 1][j - 1];}cout << C[n][m] << '\n';return 0;}
杨辉三角Pascal`s triangle
常见计数方法
特殊优先
捆绑与插空
容斥原理
https://oi-wiki.org/math/combinatorics/inclusion-exclusion-principle/#_2
Catalan numbers卡特兰数




说明:
一棵二叉树,根结点占 1 个结点,假设左子树 x 个结点,那么右子树有 n - 1 - x 个结点。
枚举 x for 0 … n-1,即可得到上面的式子。


说明:个合法的组合数,减去非法组合数
,就得到合法的组合数
卡特兰数(Catalan)公式、证明、代码、典例.
https://blog.csdn.net/sherry_yue/article/details/88364746
杨辉三角
https://www.shuxuele.com/pascals-triangle.html
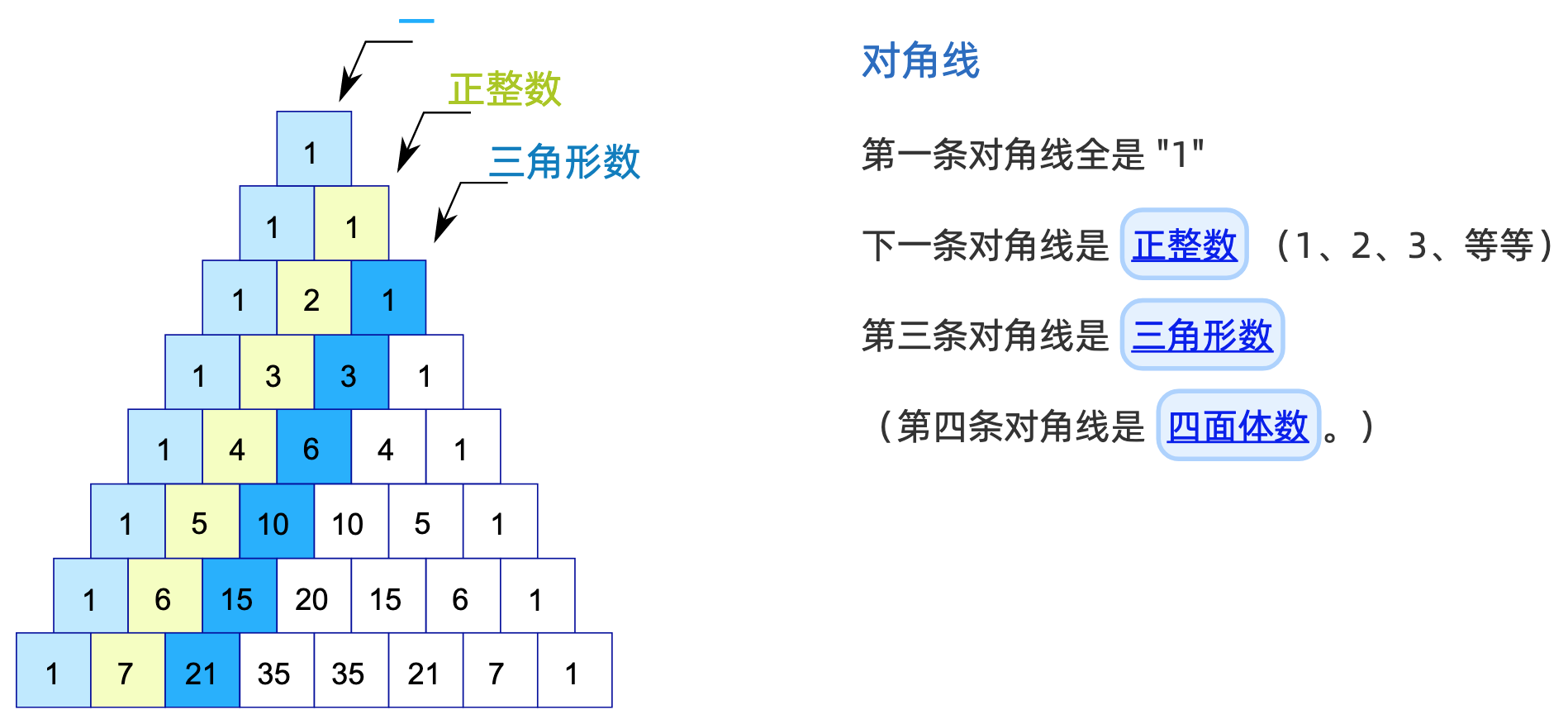


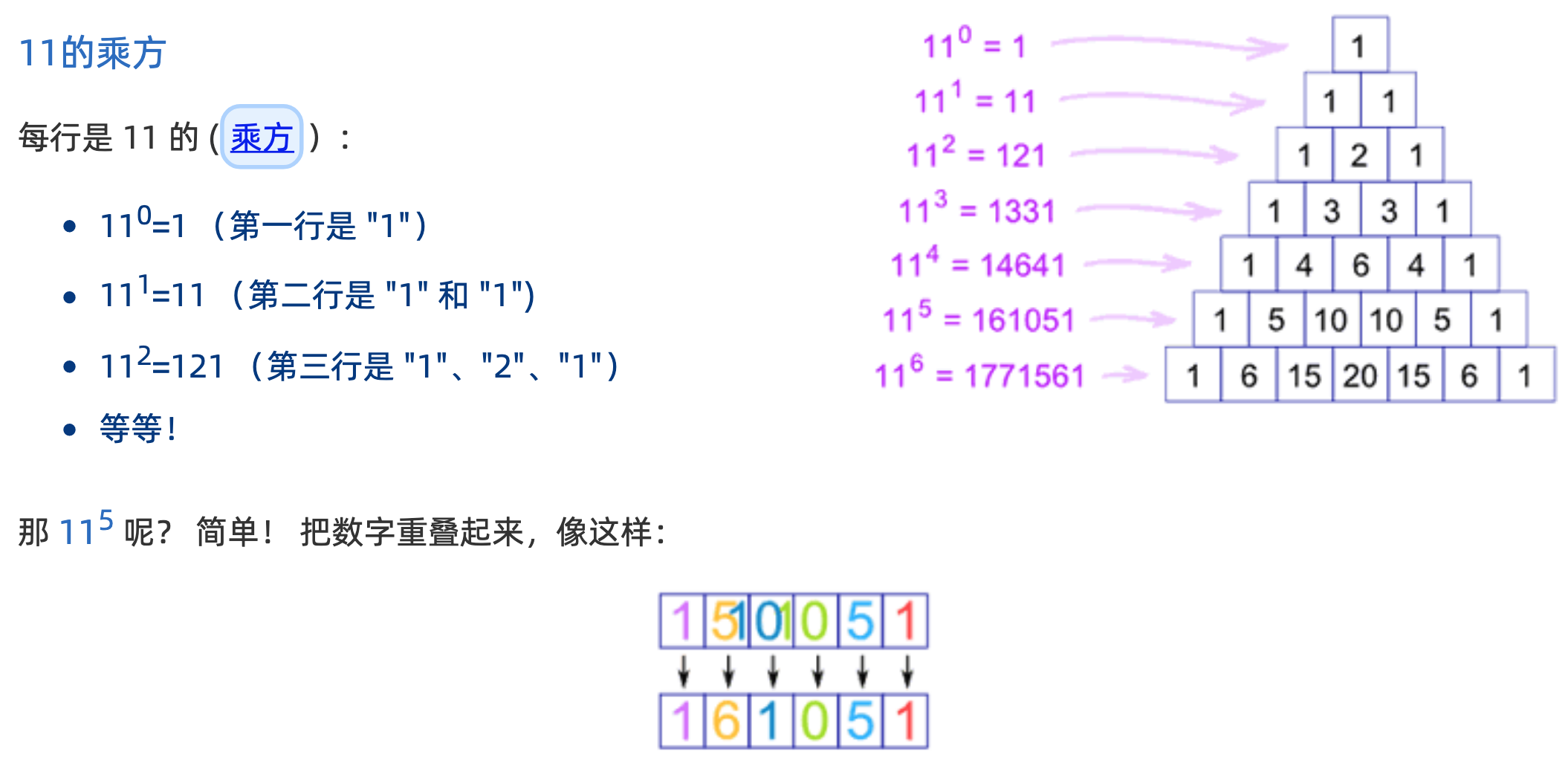

杨辉三角的应用