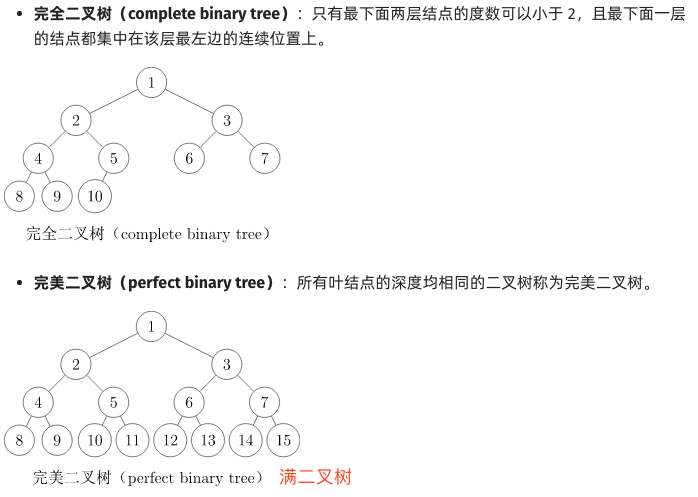
完全二叉树的定义与基本性质

image.png

完全二叉树的数组表示法

  • 对于一棵具有 n 个结点的完全二叉树，对于任意一个结点，编号为 i

if (i > 1) 父结点编号 i / 2
if (2 i > n) 没有左儿子 else 左儿子编号为 2 i
if (2 i + 1 > n) 没有右儿子 else 右儿子编号为 2 i + 1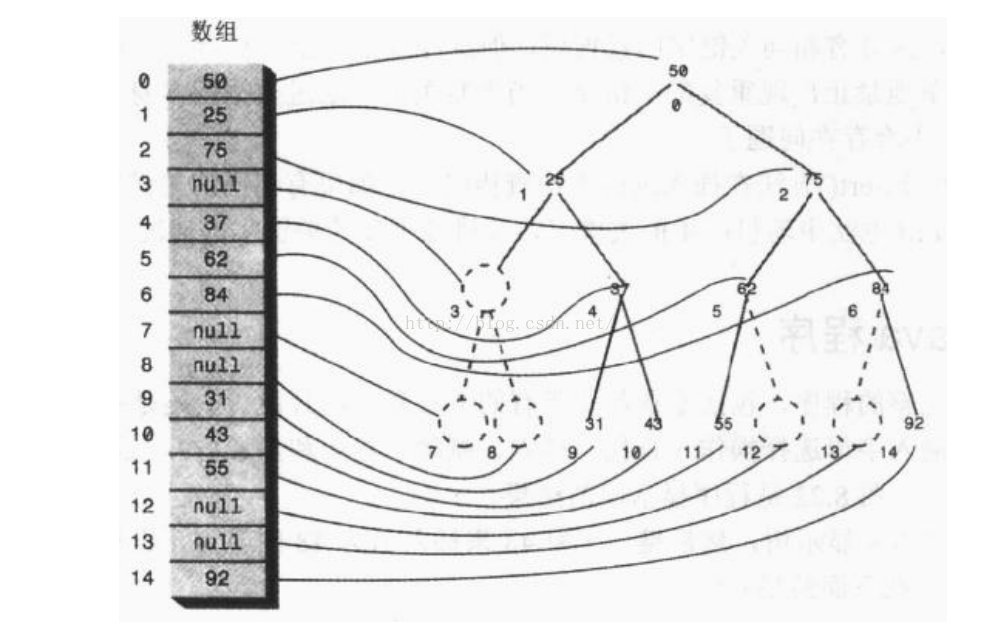
image.png

  1. #include <bits/stdc++.h>
  3. using namespace std;
  5. const int N = 1010;
  7. char data[N];
  8. int node[N];
  9. int n;
  11. void pre_order(int i){
  12.     if (data[i] == '$') return ;
  14.     if (data[i] != '$') cout << data[i];
  15.     if (i * 2 <= n) pre_order(i * 2);
  16.     if (i * 2 + 1 <= n) pre_order(i * 2 + 1);
  17. }
  19. void in_order(int i){
  20.     if (data[i] == '$') return ;
  22.     if (i * 2 <= n) in_order(i * 2);
  23.     if (data[i] != 'S') cout << data[i];
  24.     if (i * 2 + 1 <= n) in_order(i * 2 + 1);
  25. }
  27. void post_order(int i){
  28.     if (data[i] == '$') return ;
  30.     if (i * 2 <= n) post_order(i * 2);
  31.     if (i * 2 + 1 <= n) post_order(i * 2 + 1);
  32.     if (data[i] != 'S') cout << data[i];
  33. }
  35. int main(){
  36.     memset(data, '$', sizeof data);
  38.     cin >> n;         // 结点总数
  39.     for (int i = 1; i <= n; i++) cin >> data[i];  // 根结点下标是1，从上到下，从左到右输入
  41.     pre_order(1);
  42.     puts("");
  44.     in_order(1);
  45.     puts("");
  47.     post_order(1);
  48.     puts("");
  50.     return 0;
  51. }
  53. /*
  54. 输入：
  55. 3
  56. A B C
  58. 输出：
  59. ABC
  60. BAC
  61. BCA
  62. */