ST算法介绍

ST 表是用于解决 可重复贡献问题 的数据结构

ST算法，能在 O(nlogn)时间的预处理后，以O(1)的时间复杂度在线回答
"数列A中下标在l~r之间的数的最大值是多少"
这样的区间最值问题

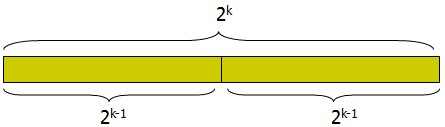
// dp[i][j]表示数列在[i, i + 2 ^ j - 1]里的最大值
// 初始状态是 dp[i][0] = a[i]
// 递推公式 dp[i][j] = max(dp[i][j - 1], dp[i + (1 << (j - 1))][j - 1])
void ST_prework(){
    for (int i = 1; i <= n; i++) dp[i][0] = a[i];
    int Log = (int)(log(1.0 * n) / log(2.0)) + 1;
    for (int j = 1; j < Log; j++)
        for (int i = 1; i <= n - (1 << j) + 1; i++)
            dp[i][j] = max(dp[i][j - 1], dp[i + (1 << (j - 1))][j - 1]);
}

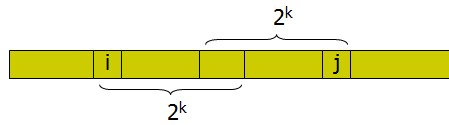
询问时，
先计算出使得2^k 小于区间长度，且最大
那么，就可以用 "从l开始的2^k个数" 和 "以r结尾的2^k个数"，这两段覆盖整个区间[l, r]
即使有重叠也没关系
int ST_query(int l, int r){
    int k = (int)(log(1.0 * (r - l + 1)) / log(2.0));
    return max(dp[l][k], dp[r - (1 << k) + 1][k]);
}

关于log的预处理

1、使用cmath的log函数，执行效率很高，影响不大。需要注意的是，参数和返回值都是double
double log (double x);
2、手动预处理
int Log[N];  // 预处理log
Log[1] = 0;
for (int i = 2; i <= n; i++) Log[i] = Log[i >> 1] + 1;

ST算法特点

ST 表
能较好的维护“可重复贡献”的区间信息（同时也应满足结合律），
时间复杂度较低，
代码量相对其他算法很小。
但是，ST 表能维护的信息非常有限，不能较好地扩展，并且不支持修改操作

例题

POJ - 3368 Frequent values