Primes and factors素数和因子

Number of primes

One interesting class of prime: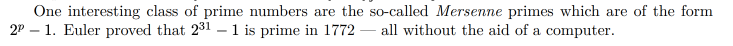

试除法判断素数

bool is_prime(int x)
{
    if (x < 2) return false;
    for (int i = 2; i <= x / i; i++)
        if (x %i == 0) return false;
    return true;
}

分解质因子

void divide(int x)
{
    for (int i = 2; i <= x / i; i++)
        if (x % i == 0)
        {
            int s = 0;  // 计数器，记录个数
            while (x % i == 0) x /= i, s++;
            cout << i << ' ' << s << endl;
        }
    if (x > 1) cout << x << ' ' << 1 << endl;
    puts("");
}

唯一分解定理

朴素筛法O(nlogn)

void get_primes(int n)
{
    for (int i = 2; i <= n; i++)
    {
        if (!st[i])
        {
            primes[cnt++] = i;
        }
        for (int j = i + i; j <= n; j += i) st[j] = true;
    }
}

埃式筛法O(n) O(nloglogn)

void get_primes(int n)
{
    for (int i = 2; i <= n; i++)
    {
        if (st[i]) continue;
        primes[cnt++] = i;
        for (int j = i + i; j <= n; j += i)
            st[j] = true;
    }
}

线性筛 O(n)

// 核心：n只会被他的最小质因子筛掉
void get_primes(int n)
{
    for (int i = 2; i <= n; i++)
    {
        if (!st[i]) primes[cnt++] = i;
        for (int j = 0; primes[j] <= n / i; j++)
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

约数个数

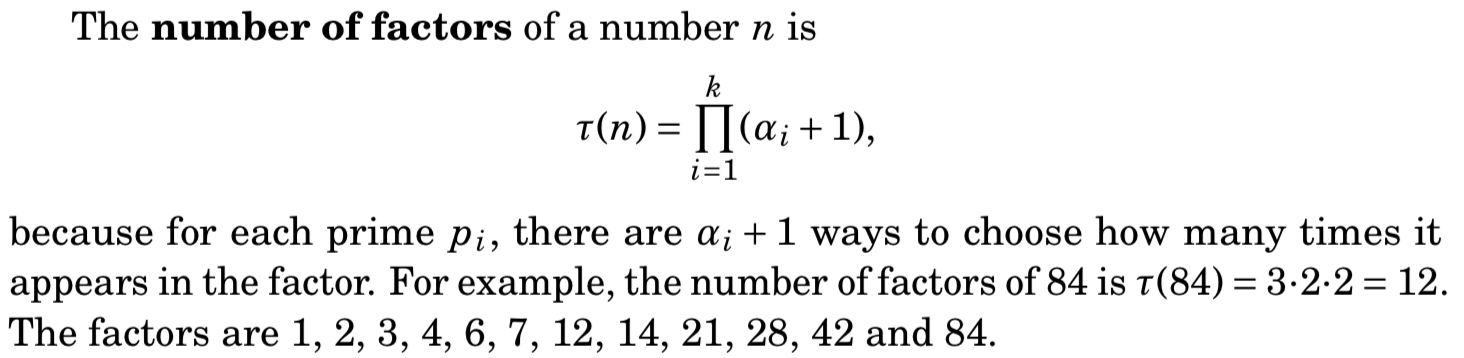
#include <iostream>
#include <unordered_map>
using namespace std;
typedef long long LL;
const int mod = 1e9 + 7;
int main()
{
    int n;
    cin >> n;
    unordered_map<int, int> primes;
    while (n--)
    {
        int x;
        cin >> x;
        for (int i = 2; i <= x / i; i++)
            while (x % i == 0)
            {
                x /= i;
                primes[i] ++;
            }
        if (x > 1) primes[x]++;
    }
    LL res = 1;
    unordered_map<int, int>::iterator it;
    for (it = primes.begin(); it != primes.end(); it++)
        res = res * ((*it).second + 1) % mod;
    cout << res << endl;
    return 0;
}

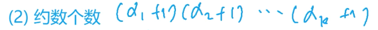
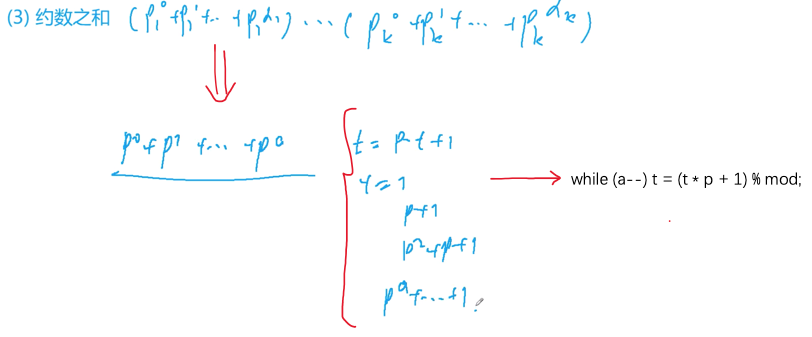
约数之和

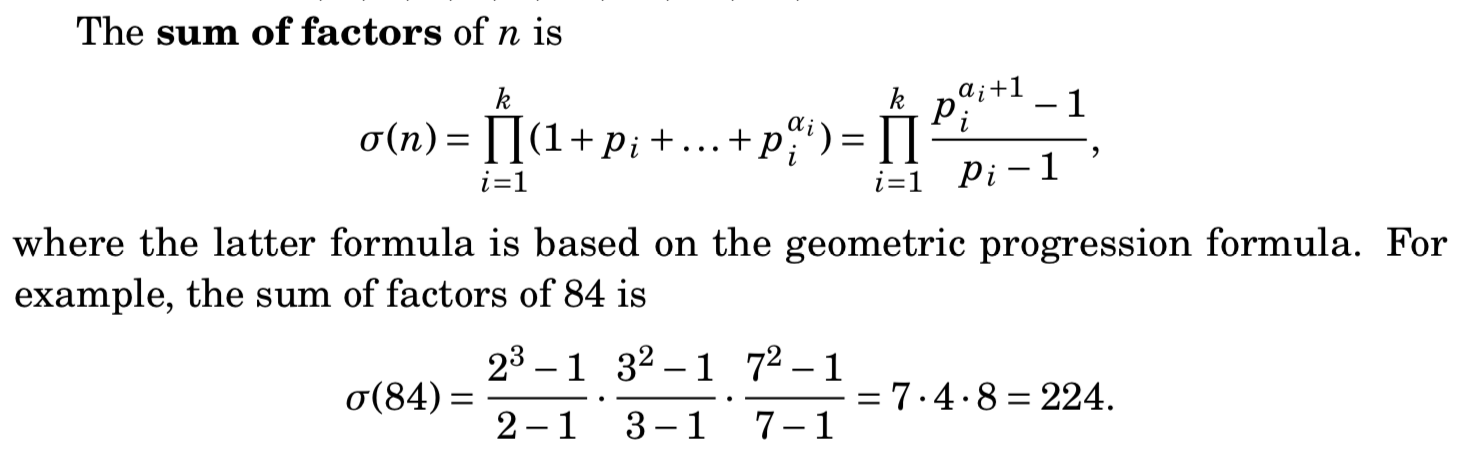
#include <iostream>
#include <algorithm>
#include <unordered_map>
using namespace std;
typedef long long LL;
const int mod = 1e9 + 7;
int main()
{
    int n;
    cin >> n;
    unordered_map<int, int> primes;
    while (n--)
    {
        int x;
        cin >> x;
        for (int i = 2; i <= x / i; i++)
            while (x % i == 0)
            {
                x /= i;
                primes[i]++;
            }
        if (x > 1) primes[x]++;
    }
    LL res = 1;
    for (auto prime : primes)
    {
        int p = prime.first, a = prime.second;
        LL t = 1;
        while (a--) t = (t * p + 1) % mod;
        res = res * t % mod;
    }
    cout << res << endl;
    return 0;
}

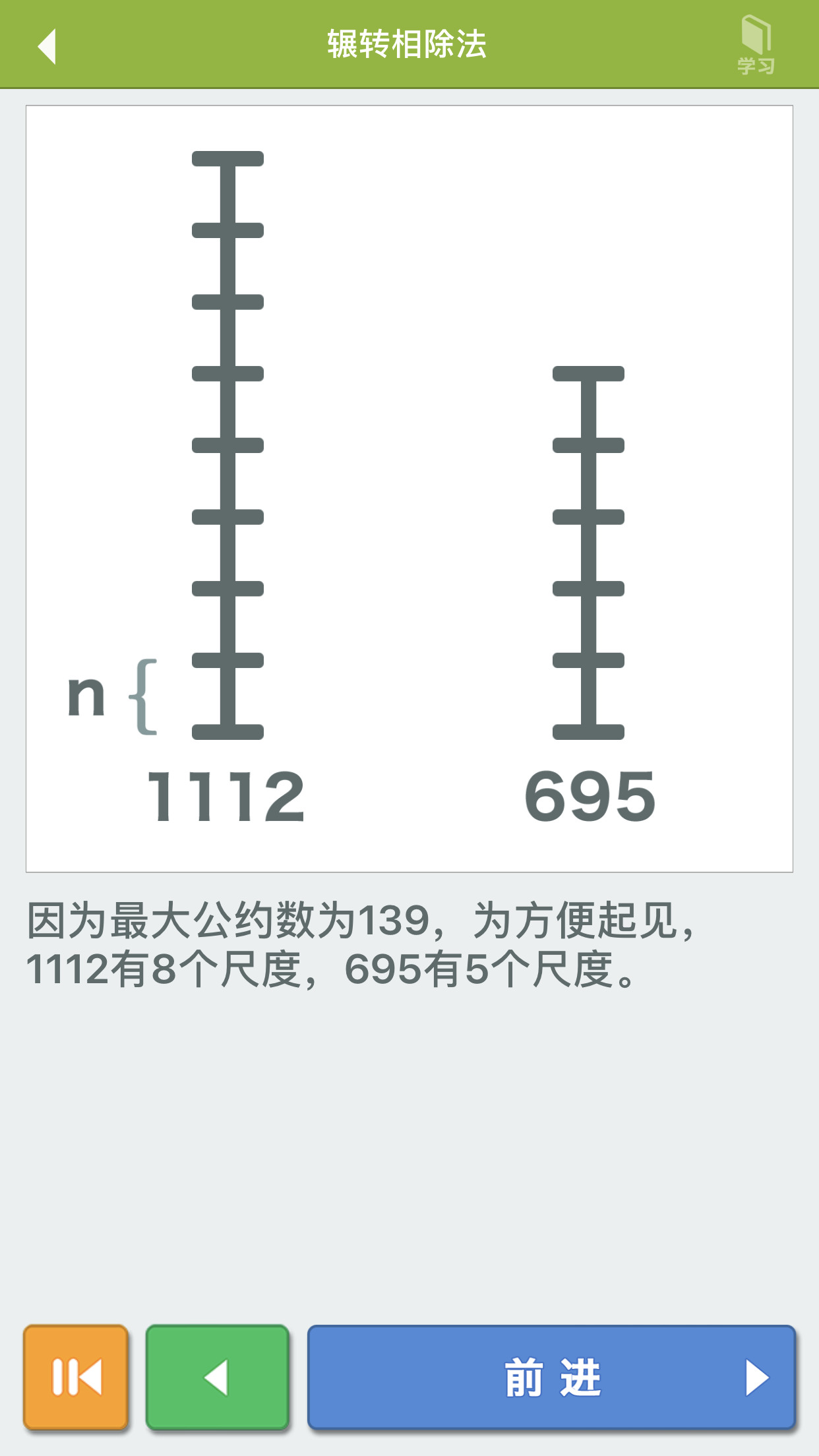
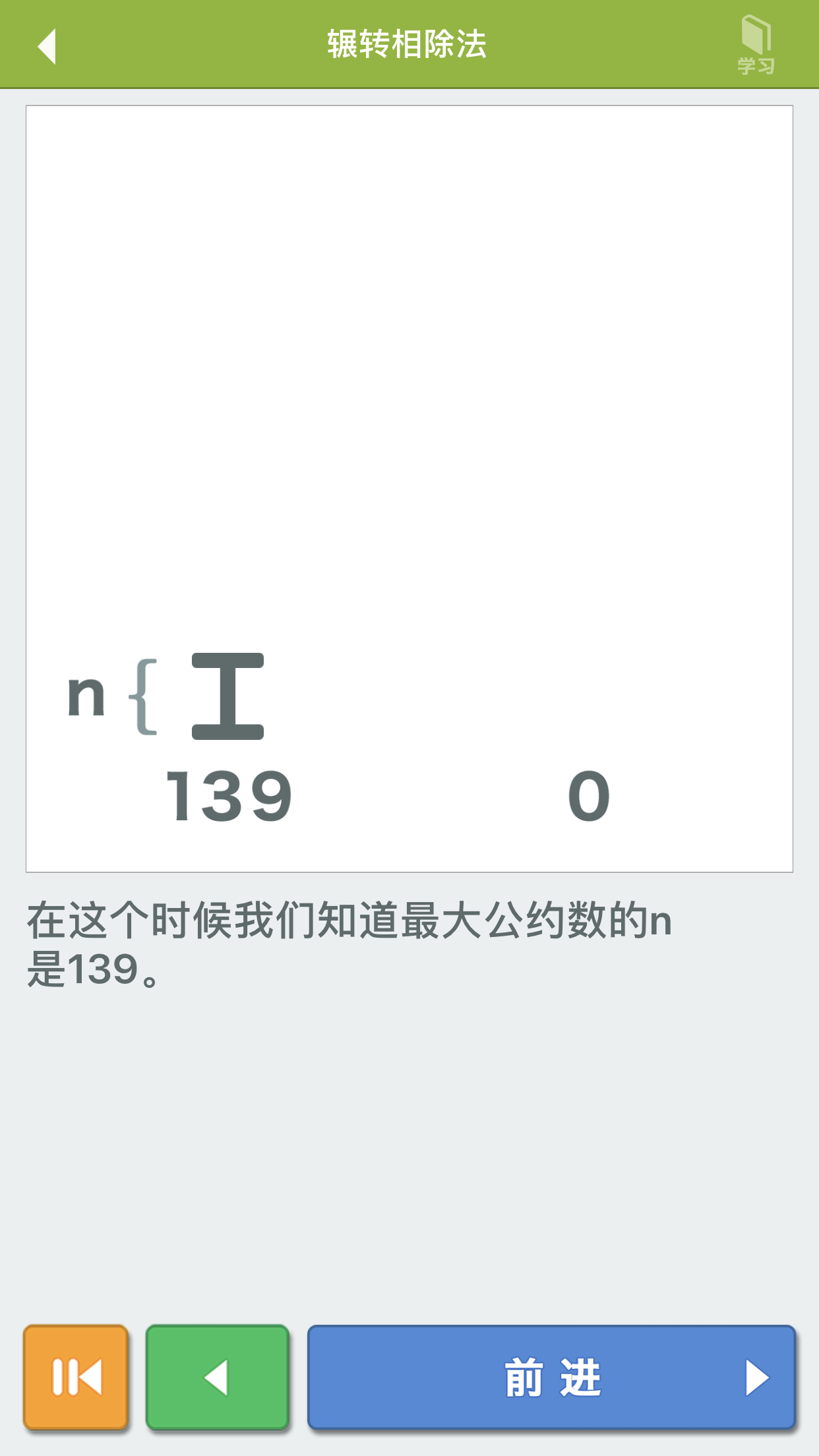
欧几里得算法(辗转相除法)

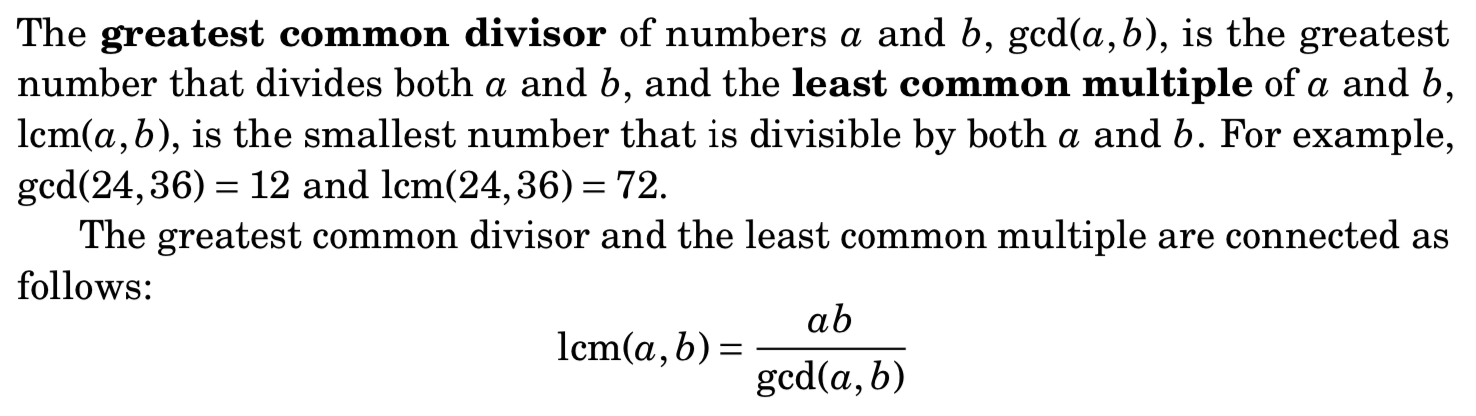
int gcd(int a, int b) {
    if (b == 0)
        return a;
    return gcd(b, a % b);
}
int gcd(int a, int b)
{
    return b ? gcd(b, a % b) : a;
}
int gcd(int a, int b) {
    int tmp;
    while(b != 0) {
        tmp = b;
        b = a % b;
        a = tmp;
    }
    return a;
}

Modular arithmetic模运算

核心：随时取模

大纲要求

•【3】整除、因数、倍数、指数、质数、合数、同余等概念

•【3】唯一分解定理

•【3】欧几里得算法（辗转相除法）

•【4】埃氏筛法和线性筛法求素数