05.探索数据和第一次比例测试

好，我们谈到了我们的研究.60个人给了我们他们最喜欢的网站的偏好。这是一个单样本比例判别法(One sample test of proportions.)。这是它的正式名称，你们可以看到，我用两个数字符号注释了那个部分和那个名字。

一个单样本比例检测

05.Exploring Data and a First Test of Proportions
image.png
image.png
比例测试就是看测试反应的比例。如果你发现自己在计算对象，例如，每个对象都给出了他们的偏好，那么你可能在做一个比例测试。这叫做一个样本，因为我们有一个样本，这个样本是他们的偏好。在一个变量偏好上，我们有他们喜欢网站A还是B的比例，这是一个单样本测试。稍后，我们还会用到双样本比例判别法。

我在这个代码编辑器中会做的是，偶尔我会高亮一行，然后点击运行，或者按control键，回车键。这会运行这行代码。它会复制它并在控制台中发出它。

当它这样做时，其中一些行会给出输出，我们也会在底部的控制台中寻找。

让我们开始吧。我们会加载prefsAB.CSV这是网站A或B的首选项，当我高亮这一行并点击运行，你会看到除了它告诉我它执行了这行之外没有任何反馈。如果我执行的任何一行有错误或警告，它们将显示在下面这里的底部。

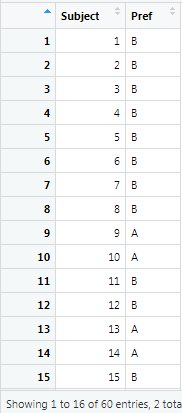
有时查看我们刚加载的东西会很好，我们说，view，按A和B，这样做时，我们会看到有一列用于对象和一列用于pref，很简单。60个受试者每人给了我们他们的偏好，不管他们是喜欢网站A还是网站b，现在我们显然不能很容易地说出可能存在的区别当我们看这个表格的时候。我们把它关掉，然后继续。我们要做的一件事是作为一种良好的练习，我们要把主语重新编码为分类因子。

变量都有不同的类型。你可以把变量想象成我们刚才看到的这些列，分类变量，有时也叫名义变量，是指只有类别的变量。这里的对象已经被编码为一个数字，我们需要告诉我们，实际上，它好像是一个字母，例如，它好像是一个名字。这样它就被认为是一个类别而不是一个数值响应变量。

然后我们可以看一下数据的摘要。我们可以看到，除了这里的6个层次外，还有54个不同的层次，总共60个层次。然后有14个A的回答，46个B的回答，似乎人们更喜欢B。但从统计学角度来看，问题是，我们在那里看到的偏好是否有显著不同?实际上，我们在一个样本测试中问的是，它是否与偶然显著不同?如果30个人喜欢A, 30个人喜欢B，我们显然会说没有区别。在我们说有显著差异之前我们离那个偶然点有多远?我们还可以使用plot命令非常简单地绘制此图。注意这里的美元符号，它告诉我们，我们要的是pref A和B中的pref列。我可以回到上面来复习一下当你习惯R是如何工作的时候提醒你这个表格是什么样子的。你现在可以看到主题了，因为数字和字母一样左对齐。思考是一个因素。顺便说一句，你也可以在prefs AB上键入is factor，美元符号访问subject作为列。现在它说的是真的。在我们重新记录之前，它会说错误。当我们看到这里的pref时，我们可以看到柱状图统计每个的数量。

皮尔森卡方检测

image.png
image.png
X的平方，是17，这是统计值。自由度是1，P值非常非常小，接近于0。这一切意味着什么呢?

与静态计算的分布有关。这里是x²分布。对于我们的目的来说，重要的是理解如果你得到一个重要的结果意味着什么，以及如何写它。这个结果实际上很重要，因为P值小于0.05。这通常被认为是一个阈值，低于这个阈值，我们就会宣布结果具有统计学意义。很明显，这里很小，远小于0.05。自由度是不同测试的参数。很多只有一个自由度，有些有两个，比如F测试，这是我们要报告的部分内容。如果你对自由度是如何计算的感兴趣，每种测试的自由度都是不同的，你可以在网上进一步查找相关细节。

所以在这一点上，我们知道事实上有一个统计上的显著差异在网站B，重新设计，和网站a，旧的网站相比，我想我们应该希望如果我们去设计一个新的网站。

06.Understanding and Reporting Your First Statistical Test

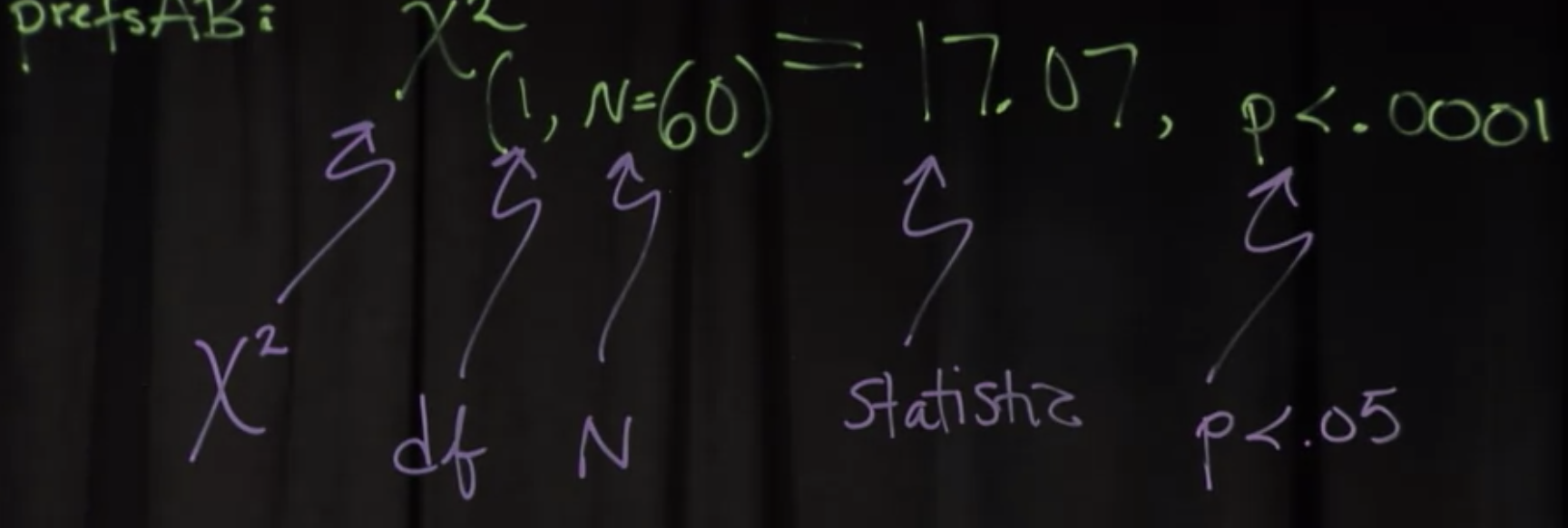
image.png
image.png
我们只需要知道p值是否小于0.05或0.01，比如小于0.0001就足够显著了，并不关心他的具体大
这样就能表明足够显著了。

p值>0.05,其实表明统计学上不显著。我们不需要标记p的具体数值，而是标记为：n.s., non-significant.

p值在0.05——0.1之间，我们也会关注，它表明了一种趋势，可能需要更多的数据和更多的测试者来说明问题；

显著：表明两个事物间有显著区别
不显著：区别不显著。并不代表他们没区别。它只说明依据我们现有的观测数据，看不出显著区别。

07.Exact Tests, Asymptotic Tests, and the Binomial Test精确检验，渐近检验，二项检验

精确检验

这是一个精确检验，叫做二项检验。卡方检验，抽样卡方检验，是渐近检验，这意味着它接近我们得到的p值。数据点越多，样本就越多，效果越好。事实上，有些人认为除非你有1000或更多的数据点否则卡方检验是不好用的。我们当然有更少的，我们只有60个，如果你还记得的话。

所以我们可以使用精确判别法，它的计算量更大，但它能给出准确的p值，二项检验就能做到这一点。我们已经完成了前面的这些步骤来创建这个prfs变量中需要的内容，因此我们只需运行二项式检验。
image.png
你可以看到这是一个精确的测试。它给出了这里的数据输出，你可以看到的p值也非常非常小。很明显，网站B比网站a更受青睐，它会给我们一些其他输出，但就我们的目的而言，我们现在不考虑这个。这就是二项式判别法，我们用60个数据点的二项式判别法来报告p值。
image.png
image.png
你可以看到我把单样本卡方检验和二项检验用红色表示在第一个表格的最上面一行。在左边这一栏，你可以看到我们对一个样本做了测试，它有两个反应类别，受试者可以说他们喜欢网站a或网站b。

以上就是我们所做的测试。如果有两个以上的响应类别怎么办?我们仍然可以使用单样本卡方检验，但如果我们想要一个精确的检验，我们需要远离只能处理两个反应类别的二项检验，而使用多项式检验。让我们回到我们的代码，继续看一下这些分析。

两个以上响应类别，精确检验不适合用二项检验，而用多项式检验。

08. More One-Sample Tests of Proportions

您可以看到，我们有一个新的数据文件要读入，abc.csv，所以现在有三个响应类别，首选项A, B和C，我们将遵循与前面类似的模式。读过文件后，我们会查看它，你可以看到左边有主题，右边有偏好，现在不仅有a和b，还有c，这是一个新的网站替代方案。从研究设计的角度来看，我们必须考虑是否是在实验结束前，因为一些人提前接触了其他两种方案，因为次序造成最后出现的方案排在最后。出于我们的目的，我们假设当前是一组新的60名参与者进行测试，他们之前没有见过另外两名参与者。
image.png
为了更好的练习，我们将重新编码主题列作为分类因素。我们也可以对数据进行总结。我们可以看到，总结中有8个网站A的偏好，比以前更少了。B是21 C是31，在某种意义上，我们可能认为C进来了，吸走了a和B的偏好，可能成为新的受欢迎的。但统计问题是，对C的31个偏好在统计上是否显著?关于B的21，很明显，它们都比A要大一些，这可能对我们很有意义，仅仅从表面上看。
我们创建了一个交叉表格，一个告诉我们偏好的表格。当我们有多个示例时，这些表就更有趣了。所以我们可以再次看到ab和c在我们的表格中然后我们再次进行x平方分布检验。我们可以看到结果是现在有两个自由度，而不是一个。
image.png
因为我们有三个反应类别所以这种x平方检验的自由度就是反应类别的数目减去1。我们还可以看到，我们的P值确实显著小于0.05。这里我为我们的三个响应类别数据添加了x平方检验结果。按(A, B, c)我们可以看到我们有X²正如我提到的我们现在有两个自由度。我们仍然有60个对象，60个样本。卡方统计量是13.30,p值小于0.01。这就是我们报告第二个结果的方式。你可以从这里推断出所有你可能做的x平方分布测试。这就是渐近检验。我们提到的多项式判别法是一个精确的判别法为此我们需要加载x项库。做一下。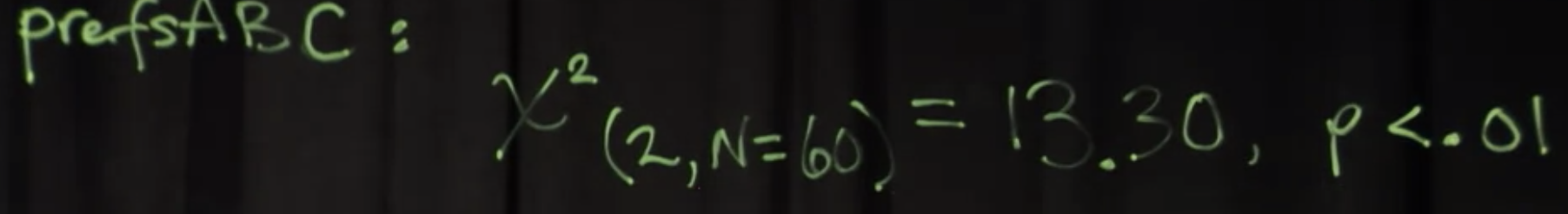
image.png

x多功能函数给出了一系列概率的检验。我们在测试我们的偏好。c函数只创建一个列表。所以我们可以传入一列值，这些值是没有偏好时的概率。那就是三分之一的受访者将为每个类别,A,B和C如果没有偏爱的任何网站,我们预计三分之一的人喜欢他们每个人,然后这个函数有多种方式来计算通过的概率和统计的名字。
image.png
不知道的函数，可以先输入？再输入函数名来查询。

顺便说一句，如果你想查询任何函数的信息，在我们的演播室里一个非常有用的东西就是输入一个问号，然后输入你感兴趣的函数。假设我们不知道stat name参数是什么意思我们想知道更多我们可以输入问号xmulti。我们可以看到，我知道在你的屏幕上，字体可能非常小，但它是一个帮助页面，给我们所有关于这个函数和它的参数的信息。这是学习更多知识的好方法。

So, let’s go ahead and execute the x multifunction, the multinomial distribution test, multinomial test, and we can see it gives us a p value, that’s an exact p value. Also quite a bit less than 0.05. So, again, we’d expect a difference, given those proportions. Now, what that tells us, is there is a difference between some levels of some numbers, of A, B, and C. It doesn’t actually tell us what the difference is between A and B, B and C, or A and C. Those pair wise differences are what are called post hoc tests or post hoc pair wise comparisons. They’re post hoc in the sense that they follow a statistically significant overall, or what’s called omnibus test. We just did that omnibus test, with the multi nomial test, with x multi. If we want to know about the comparison of the separate differences, well then we can go ahead and run post hoc binomial tests, binomial again in sense that now we’re just back to testing each of them against a hypothesized probability.

那么，让我们继续执行x多项式函数，多项式分布判别法，多项式判别法，我们可以看到它给了我们一个p值，一个确切的p值。也比0.05小一些。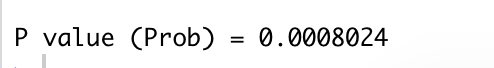
image.png
所以，我们现在知道ABC是有显著差异的（但我们并不知道具体A和B，B和C，A和C的差异有多少）。那些成对的差异是所谓的事后测试或事后的成对比较。他们是事后的，因为他们遵循了统计上的显著性，也就是所谓的综合测试。我们刚刚用多元判别法做了综合判别法，用x的多元判别法。如果我们想知道单独差异的比较，那么我们可以进行后二项检验，二项检验也就是说，现在我们只是用假设的概率来检验它们。

例如，我们可以在这条线中看到a水平测试和假设概率1 / 3的对比。
如果我们知道这个测试所显示的是，我们把偏好a的行加起来，把它们和表中的所有行进行比较。把它和1 / 3的概率进行比较。我们对所有的A, B, C水平都这样做，来看看哪些是明显不同于随机的。我们将把所有这些结果存储在AA BB CC中，然后我们将继续做所谓的调整。并报告结果。现在需要对这种调整做一点解释。

当我们进行统计检验时，我们说如果p小于0.05，就会有显著的结果，这意味着有1 / 20的概率，我们可能认为有统计上显著的结果，但实际上只是偶然。0.05的概率是1 / 20。如果我们做多重比较，如果我们做20次，我们会期望1次碰巧是显著的。所以我们必须为此做出调整。我们用Bonferroni校正。这里的方法称为home，它实际上是首选方法。它包含了Bonferroni，但它不是一个严格的测试。这是一个顺序测试，根据p值的低程度调整每个p值。第一个p值是3
image.png
第一个p值在这个例子中是三次测试乘以三，所以增加了三次。第二个是翻倍的，最大的还是原样。如果其中任意一点不小于0.05，序列就停止。这叫做Holm的顺序Bonferroni程序。所以底线是，任何时候我们做多个测试，我们都想用这种方式进行修正。现在我们可以看到，我们有一个显著的结果a，它与1 / 3的概率显著不同。人们不喜欢它，它只有八种偏好。
对B的偏好是21，这是接近概率的，然后对C的偏好是31，这是超过一半的参与者。当然，21几乎是60的三分之一。这就告诉我们它们是否与个别的概率有显著的不同，我们看到A较低，C较高。

09. Two-Sample Tests of Proportions

我们问是否有多个样本(sample)，目前为止我们看到的测试只是针对偏好的一个样本，但如果我们有多个呢?在这些不同的样本中，我们是否可能有两个以上的反应类别?对于这些，我们需要进行两次比例抽样检验。或者一般来说，按比例结束样本检验。当我们重新访问有网站A或网站B偏好的数据文件时，我们可以在这里讨论这个。
但是现在，我们还要加上受访者的性别，他们是男性还是女性。我们来加载prefs AB性别它会给我们这些信息我们会看看男性和女性的偏好是否有差异。
image.png
我们能采集到的样本sample有2类，分别是偏好类型，性别类型。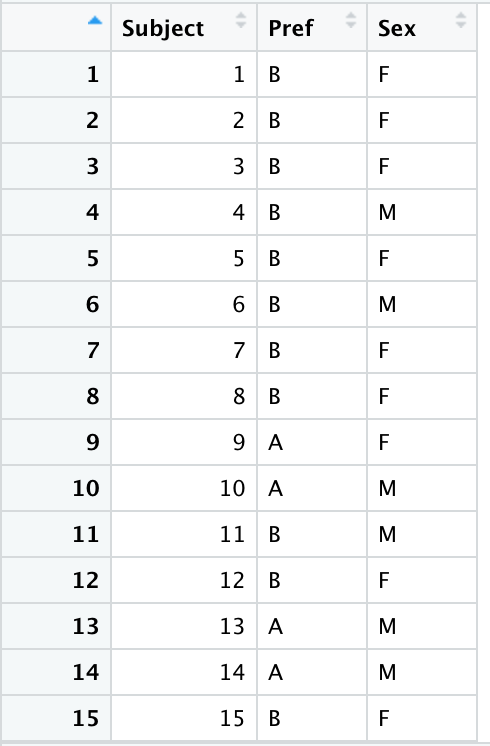
image.png
作为一个好的实践，我们将subject重新编码为一个因子而不是一个数值，因为它只是一个数字或者认为它只是一个数值。
创建男性、女性偏好的交叉表：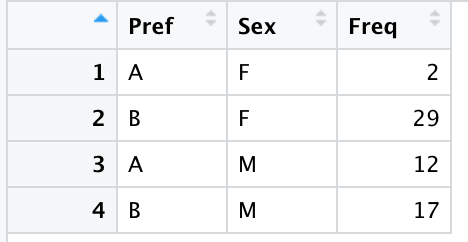
image.png
总计仍是60人。

执行皮尔森卡方统计结果：得知统计性显著。

image.png
image.png

G测试：渐进测试，是卡方的进阶，测试更准确

image.png
执行结果：
image.png

fisher’s 精确检验

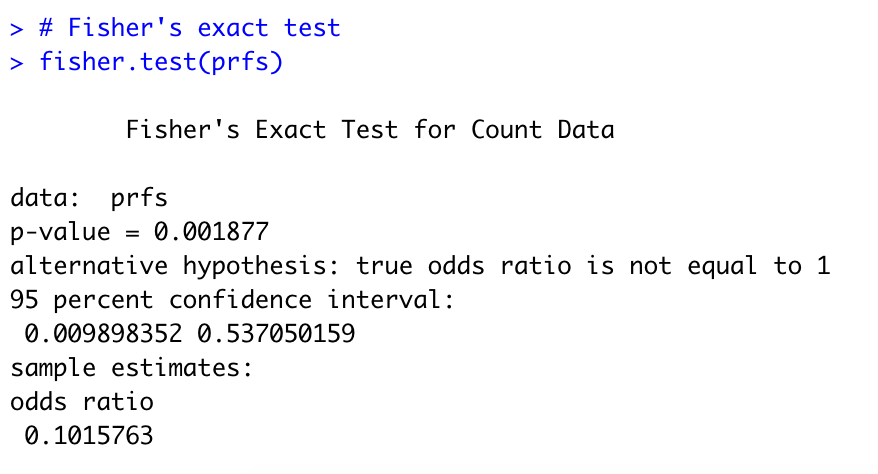
image.png
image.png

如果我们有三个响应？人们喜欢ABC，并且知道他们的性别。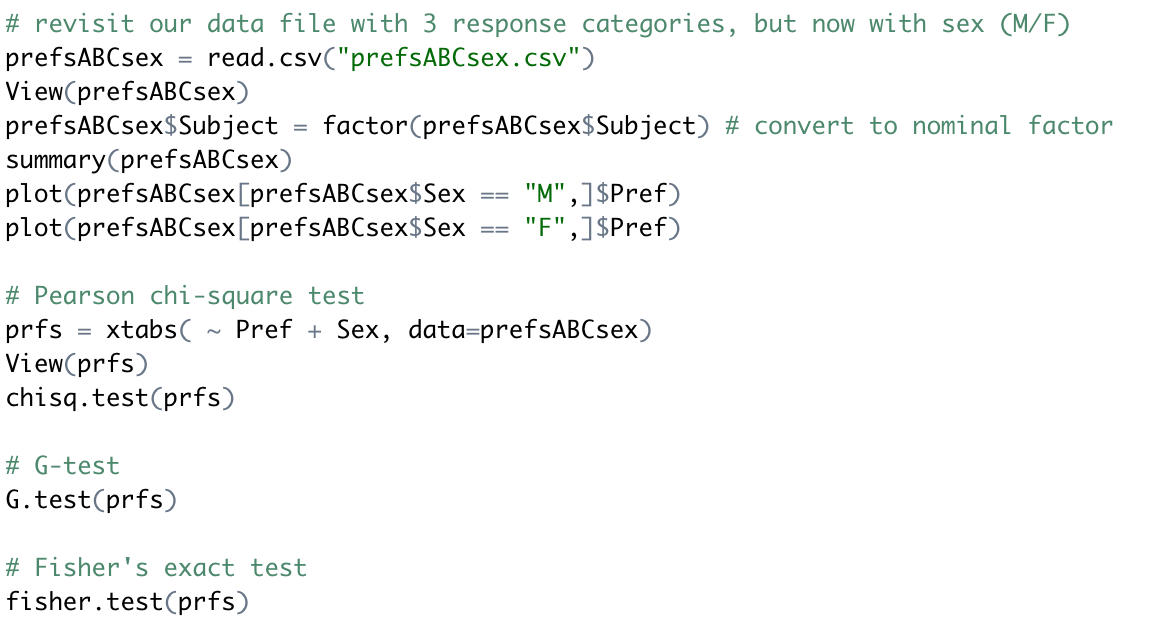
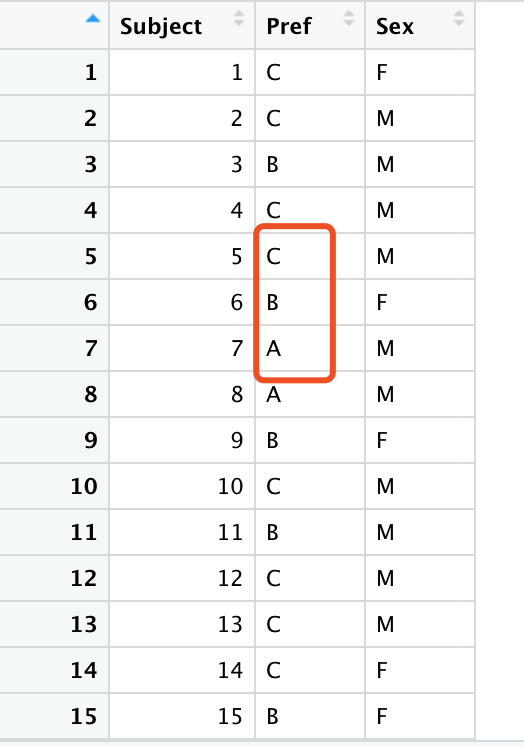
image.png
image.png
创建交叉表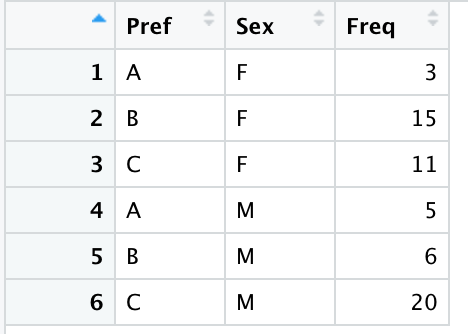
image.png

image.png
我们得出p值<0.05;

测试G-test，Fisher’s test: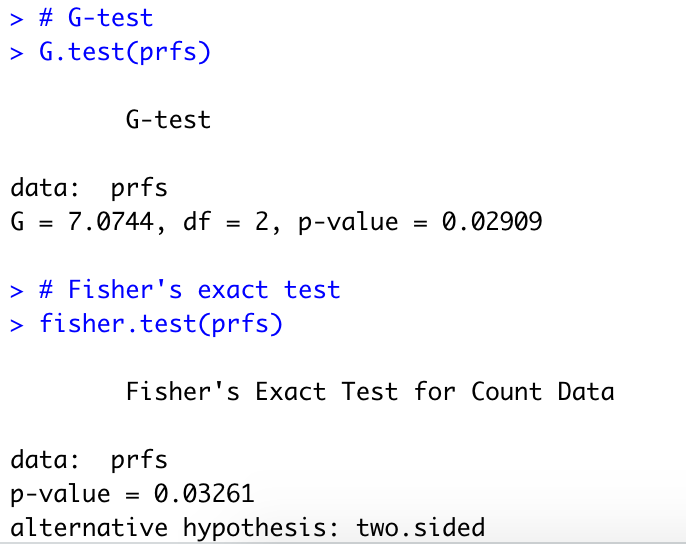
image.png
这三组测试结果相似，同样，值也是<0.05;这会给我们信息，得出相同的结论。

我们了解了确实是存在差异，但并不知道差异具体在哪里。可以执行“后检测”。
女性偏好ABC
男性偏好ABC
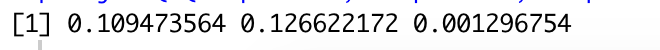
image.png
image.png
对男性，偏好ABC的差异均不显著。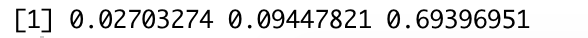
image.png
女性也同样。
我们现在讲解的是下面第三行的内容。
image.png

接下来我们会讲方差分析，这在实验中更常见实验对象给出的比他们的偏好更多。他们实际执行任务，我们测量这些任务，然后分析结果。我们下一讲。