1.1 超参数的调试（调参）

超参数有哪些？学习率α、动量梯度下降法参数β、Adam算法参数（β1、β2、ε）、神经网络的层数、神经网络各隐层的节点数、学习率衰减系数、mini-batch大小等
image.png
随机选择超参数一般胜过表格法（按照表格中的调整值一步步调整各参数，效率较低）
image.png
使用由粗到细的方法（coarse to fine）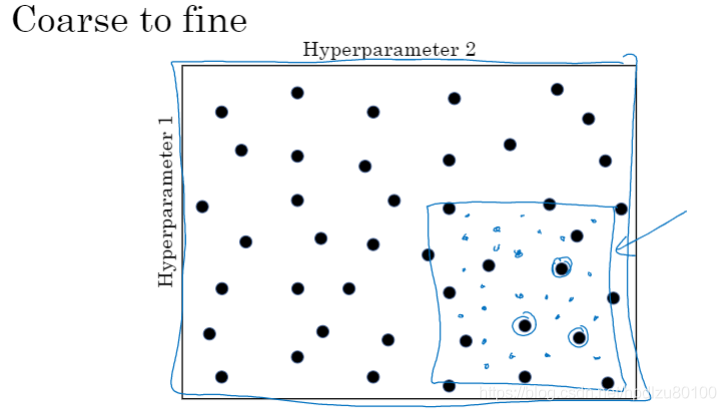
image.png

1.2 为超参数选择合适的范围

使用普通刻度（均匀刻度，uniform scale）随机选择超参数，如神经网络的层数、神经网络各隐层的节点数
image.png
选择合适的超参数刻度（如，学习率可使用对数刻度，而不是均匀分布的普通刻度）image.png
对于指数加权平均数（如，动量梯度下降参数β），应使用指数刻度而不是均匀刻度。如果使用均匀刻度，会发现当β接近1时，模型受更多数据量的影响，如，β从0.999提高到0.9995时，要考虑的历史数据量从1000上升到了2000，远高于β从0.9000提高到0.9005时的情况。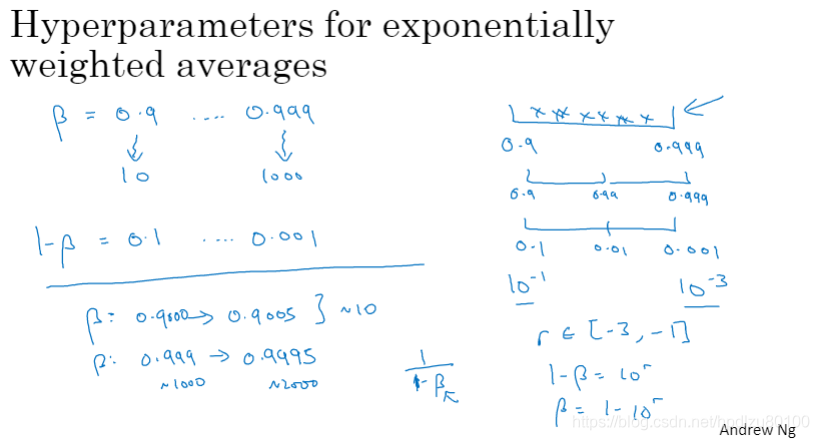
image.png

1.3 超参数训练的实践：Pandas VS Caviar

可从跨学科领域获取灵感（cross-fertilization），重新调整超参数
image.png
两种调参方式：熊猫育子方式（Panda）和鱼子方式（Caviar）
熊猫方式：针对一个模型精心调节参数，让其变得更优秀
鱼子方式：并行训练多个模型，选择最好的模型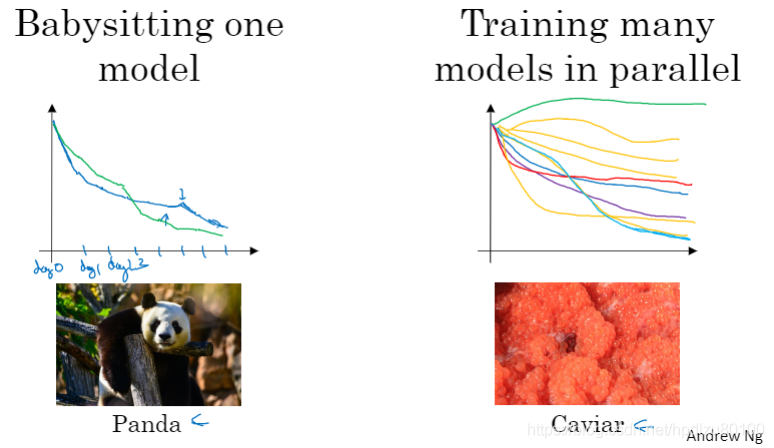
image.png

1.4 正则化网络的激活函数

正则化输入可以加速学习过程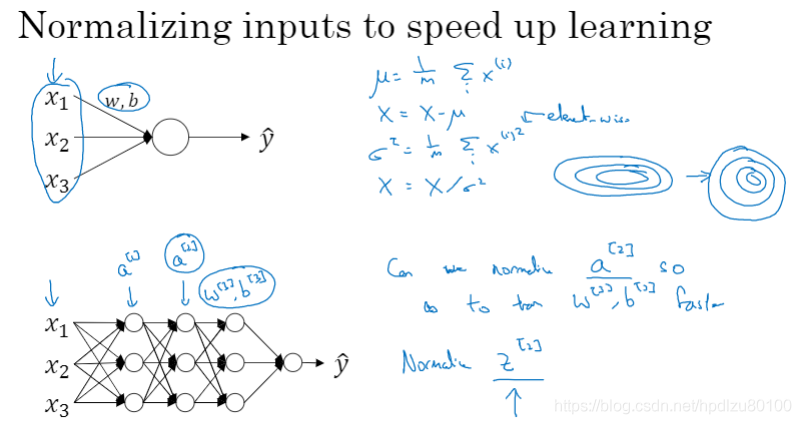
image.png
Batch Norm（批次正则化、批次归一化）的实现
image.png

1.5 在神经网络中应用Batch Norm

在神经网络中加入Batch Norm处理（介于线性值Z和激活函数a之间）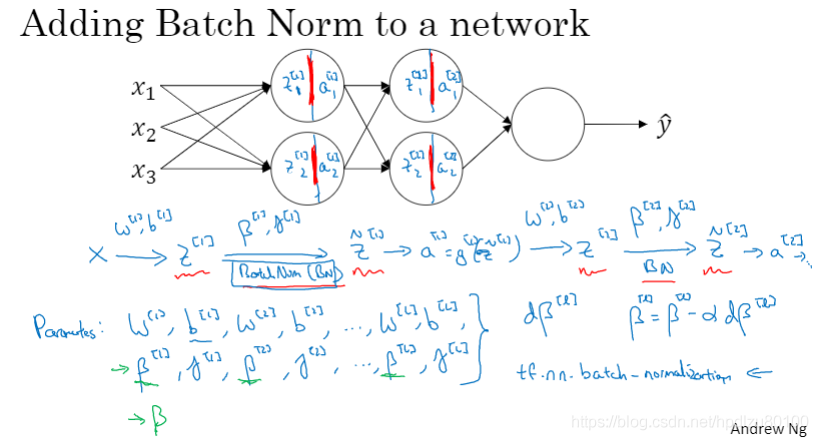
image.png
在mini-batch中使用Batch Norm（由于引入了Batch Norm参数β和γ，Z中的偏移项b可以省略或置零）
image.png
引入Batch Norm后梯度下降的实现
image.png