C1W2——神经网络基础——练习题

Note: The output of a neuron is a = g(Wx + b) where g is the activation function (sigmoid, tanh, ReLU, …).



Note: “*” operator indicates element-wise multiplication. Element-wise multiplication requires same dimension between two matrices. It’s going to be an error.

Ans: C（注意：截图所示答案D错误，正确答案为C）
Note: A stupid way to validate this is use the formula Z^(l) = W^(l)A^(l) when l = 1, then we have
- A^(1) = X
- X.shape = (n_x, m)
- Z^(1).shape = (n^(1), m)
- W^(1).shape = (n^(1), n_x)

Ans: D

Ans: B

Ans: B

1. What does a neuron compute?

• A neuron computes an activation function followed by a linear function (z = Wx + b)
• A neuron computes a linear function (z = Wx + b) followed by an activation function
• A neuron computes a function g that scales the input x linearly (Wx + b)
• A neuron computes the mean of all features before applying the output to an activation function

Note: The output of a neuron is a = g(Wx + b) where g is the activation function (sigmoid, tanh,ReLU, …).

1. Which of these is the “Logistic Loss”?
   
   Note: We are using a cross-entropy loss function.

2. Suppose img is a (32,32,3) array, representing a 32x32 image with 3 color channels red, green and blue. How do you reshape this into a column vector?
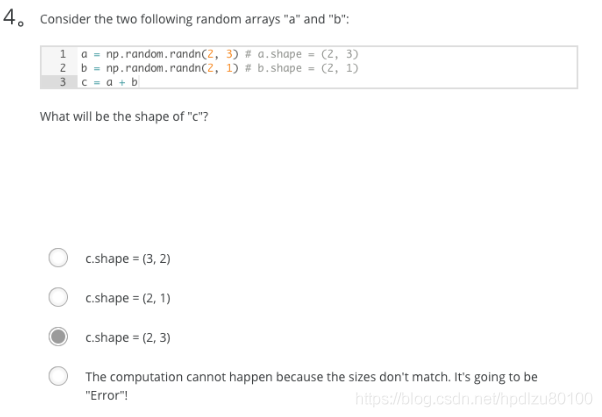
   x = img.reshape((32 * 32 * 3, 1))

3. Consider the two following random arrays “a” and “b”:
   a = np.random.randn(2, 3) _# a.shape = (2, 3)_
b = np.random.randn(2, 1) _# b.shape = (2, 1)_
c = a + b
   What will be the shape of “c”?
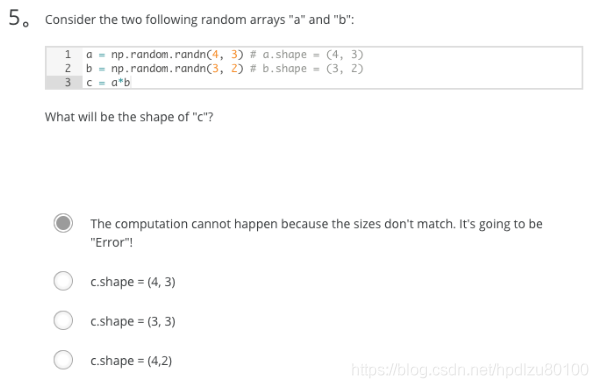
   b (column vector) is copied 3 times so that it can be summed to each column of a. Therefore, c.shape = (2, 3).

4. Consider the two following random arrays “a” and “b”:
   a = np.random.randn(4, 3) _# a.shape = (4, 3)_
b = np.random.randn(3, 2) _# b.shape = (3, 2)_
c = a * b
   What will be the shape of “c”?
   “*” operator indicates element-wise multiplication. Element-wise multiplication requires same dimension between two matrices. It’s going to be an error.

5. Suppose you have n_x input features per example. Recall that X=[x^(1), x^(2)…x^(m)]. What is the dimension of X?

(n_x, m)
Note: A stupid way to validate this is use the formula Z^(l) = W^(l)A^(l) when l = 1, then we have

• A^(1) = X
• X.shape = (n_x, m)
• Z^(1).shape = (n^(1), m)
• W^(1).shape = (n^(1), n_x)

1. Recall that np.dot(a,b) performs a matrix multiplication on a and b, whereas ab performs an element-wise multiplication.
   Consider the two following random arrays “a” and “b”:
   a = np.random.randn(12288, 150) _# a.shape = (12288, 150)_
b = np.random.randn(150, 45) _# b.shape = (150, 45)_
c = np.dot(a, b)
   What is the shape of c?
   *c.shape = (12288, 45), this is a simple matrix multiplication example.

2. Consider the following code snippet:
   _# a.shape = (3,4)_
_# b.shape = (4,1)_
for i in range(3):
for j in range(4):
c[i][j] = a[i][j] + b[j]
   How do you vectorize this?
   c = a + b.T

3. Consider the following code:
   a = np.random.randn(3, 3)
b = np.random.randn(3, 1)
c = a * b
   What will be c?
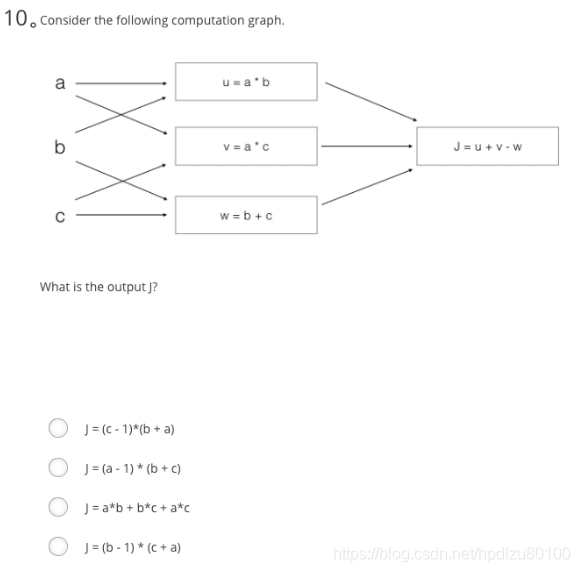
   This will invoke broadcasting, so b is copied three times to become (3,3), and ∗ is an element-wise product so c.shape = (3, 3).

4. Consider the following computation graph.
   What is the output J?

J = u + v - w
= a * b + a * c - (b + c)
= a * (b + c) - (b + c)
= (a - 1) * (b + c)
Answer: (a - 1) * (b + c)