1. import numpy as np
    2. import pandas as pd
    1. data = pd.read_csv(r"dataset/boston.csv", header=0)
    2. # data.drop(["class"], axis=1, inplace=True)
    3. data.head()
    2.     Unnamed: 0    crim    zn        indus    chas    nox        rm        age        dis        rad    tax    ptratio    black    lstat    medv
    3. 0    1            0.00632    18.0    2.31    0        0.538    6.575    65.2    4.0900    1    296    15.3    396.90    4.98    24.0
    4. 1    2            0.02731    0.0        7.07    0        0.469    6.421    78.9    4.9671    2    242    17.8    396.90    9.14    21.6
    5. 2    3            0.02729    0.0        7.07    0        0.469    7.185    61.1    4.9671    2    242    17.8    392.83    4.03    34.7
    6. 3    4            0.03237    0.0        2.18    0        0.458    6.998    45.8    6.0622    3    222    18.7    394.63    2.94    33.4
    7. 4    5            0.06905    0.0        2.18    0        0.458    7.147    54.2    6.0622    3    222    18.7    396.90    5.33    36.2
    1. class LinearRegression:
    2.     '''使用梯度下降回归算法'''
    3.     def __init__(self, learning_rate, times):
    4.         '''初始化
    5.         parameters
    6.         -----
    7.         learn_rate: 学习率。梯度下降步长 
    8.         times: 迭代次数
    9.         '''
    10.         self.learning_rate = learning_rate
    11.         self.times = times
    12.     def fit(self, X, y):
    13.         '''对样本进行预测
    14.         Parameters:
    15.         X: 特征矩阵，可以是List也可以是Ndarray，形状为： [样本数量,特征数量]
    16.         y: 标签数组
    17.         '''
    18.         X = np.asarray(X)
    19.         y = np.asarray(y)
    20.         # 创建权重，初始值为0(也可以试试其他值)，* 长度比X特征数多1，多出的就是w0
    21.         self.w_ = np.zeros(1 + X.shape[1]) # X.shape[1] 为特征数
    22.         # 创建损失值列表，用来每次迭代的损失值。
    23.         # 损失值计算公式：(1/2 )*( 预测值 - 真实值)^2
    24.         self.loss_ = []
    25.         # 开始迭代
    26.         for x in range(self.times):
    27.             # 为什么使用 self.w_[1:] ？ 因为X特征个数比w少1个，所以这里w0先去掉，点乘后再加上
    28.             # 矩阵可以使用*运算，但是这里是ndarray数组只能用点乘，1表示x0
    29.             y_hat = np.dot(X, self.w_[1:]) + self.w_[0]
    30.             # 计算误差
    31.             error = y - y_hat
    32.             # 将损失值加入损失列表
    33.             self.loss_.append(np.sum(error**2)/2)
    34.             # 根据差距调整权重w_
    35.             # 调整为 w(j)=w(j)+learn_rate*sum((y - y_hat)*x(j))
    36.             # 更新w0，x看成1直接更新
    37.             self.w_[0] += self.learning_rate * np.sum(error * 1)
    38.             # ****************************************************
    39.             # ************  重点：这里一定要搞明白 ***************
    40.             # ****************************************************
    41.             # 使用x1到xn的某一列向量(即某一特征)的转置来更新w，也就是将w向x进拟合
    42.             self.w_[1:] += self.learning_rate * np.dot(X.T, error)
    43.     def predict(self, X):
    44.         '''根据参数进行预测
    45.         Paramaters
    46.         -----
    47.         X： [样本数量, 特征数量]
    48.         -----
    49.         Returns: 预测结果
    50.         '''
    51.         X = np.asarray(X)
    52.         result = np.dot(X, self.w_[1:]) + self.w_[0]
    53.         return result
    1. class StandardScaler:
    2.     '''对数据集进行标准化处理'''
    3.     def fit(self, X):
    4.         '''根据传递的样本，计算每个特征列的均值和标准差
    5.         Parameters
    6.         -----
    7.         X: 训练数据。用来计算均值和标准差
    8.         '''
    9.         X = np.asarray(X)
    10.         self.std_ = np.std(X, axis=0) # 按列计算标准差
    11.         self.mean_ = np.mean(X, axis=0) # 按列计算#值
    12.     def transform(self, X):
    13.         '''对给定数据进行标准化处理
    14.         * 将X每一列都变成标准正太分布的形式，即满足均值为0，标准差为1
    15.         * 标准化也叫标准差标准化，经过处理的数据符合标准正态分布。
    17.         Parameters
    18.         -----
    19.         X: 类数组类型。待转换的数据
    20.         '''
    21.         return (X - self.mean_) / self.std_
    22.     def fit_transform(self, X):
    23.         ''' fit后transform
    24.         '''
    25.         self.fit(X)
    26.         return self.transform(X)
    1. lr = LinearRegression(learning_rate=0.001, times=20)
    2. t = data.sample(len(data), random_state=0)
    3. train_X = t.iloc[:400, :-1]
    4. train_y = t.iloc[:400, -1]
    5. test_X = t.iloc[400:, :-1]
    6. test_y = t.iloc[400:, -1]
    7. lr.fit(train_X, train_y)
    8. result = lr.predict(test_X)
    9. # display(result)
    10. display(np.mean((result - test_y)**2))
    11. display(lr.w_)
    12. display(lr.loss_)

    1.1804176210461773e+210

    array([-2.68833075e+099, -7.57608494e+101, -1.29174503e+100,
    -2.67102000e+100, -3.24034515e+100, -1.81386180e+098,
    -1.52555272e+099, -1.67597187e+100, -1.90402088e+101,
    -9.69839266e+099, -3.06079801e+100, -1.19382162e+102,
    -5.02206239e+100, -9.48116678e+101, -3.57226707e+100])

    [116831.44,
    2083552221174028.0,
    4.883479637283036e+25,
    1.14536821770387e+36,
    2.686348040018552e+46,
    6.300564127408661e+56,
    1.477735116047291e+67,
    3.465881830645266e+77,
    8.128883677155966e+87,
    1.9065494170189406e+98,
    4.4716234404365476e+108,
    1.0487751334726054e+119,
    2.4597985390359684e+129,
    5.769214638613026e+139,
    1.353112339006075e+150,
    3.1735914100271017e+160,
    7.443345350908508e+170,
    1.7457631703262697e+181,
    4.09451517185836e+191,
    9.603281119422997e+201]

    1. # 为了避免每个特征数量级的不同对梯度下降造成的影响。我们对每个特征进行标准化
    2. lr = LinearRegression(learning_rate=0.0005, times=20)
    3. t = data.sample(len(data), random_state=0)
    4. train_X = t.iloc[:400, :-1]
    5. train_y = t.iloc[:400, -1]
    6. test_X = t.iloc[400:, :-1]
    7. test_y = t.iloc[400:, -1]
    9. # 标准化
    10. ss = StandardScaler()
    11. train_X = ss.fit_transform(train_X)
    12. test_X = ss.fit_transform(test_X)
    13. ss2 = StandardScaler()
    14. train_y = ss2.fit_transform(train_y)
    15. test_y = ss2.fit_transform(test_y)
    17. # 训练 预测
    18. lr.fit(train_X, train_y)
    19. result = lr.predict(test_X)
    20. display(np.mean((result - test_y)**2))
    21. display(lr.w_)
    22. display(lr.loss_)

    0.14911890500740144

    array([ 1.47715173e-16, -2.67726470e-03, -7.77999440e-02, 3.22218582e-02,
    -4.15123849e-02, 7.21847299e-02, -1.22496354e-01, 3.18411097e-01,
    -8.44203177e-03, -2.09306424e-01, 1.02744566e-01, -5.29297011e-02,
    -1.81988334e-01, 9.71339528e-02, -3.93923586e-01])

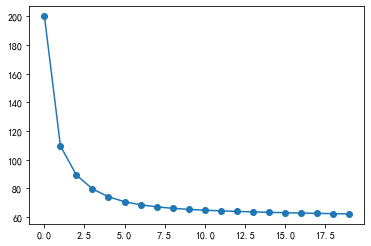
    [200.0, 109.56340745551384,
    89.24537638439179,
    79.69665810311717,
    74.15994999919499,
    70.76479029645887,
    68.5986097420355,
    67.15477786507567,
    66.1444617646852,
    65.4007703140392,
    64.82595473196506,
    64.36185638542904,
    63.973228857262946,
    63.638247945534275,
    63.343061508525125,
    63.07862649070146,
    62.83885168788381,
    62.619493019046615,
    62.41748706751545,
    62.23054285212329]

    1. import matplotlib as mpl
    2. import matplotlib.pyplot as plt
    3. mpl.rcParams["font.family"] = "SimHei"
    4. mpl.rcParams["axes.unicode_minus"] = False
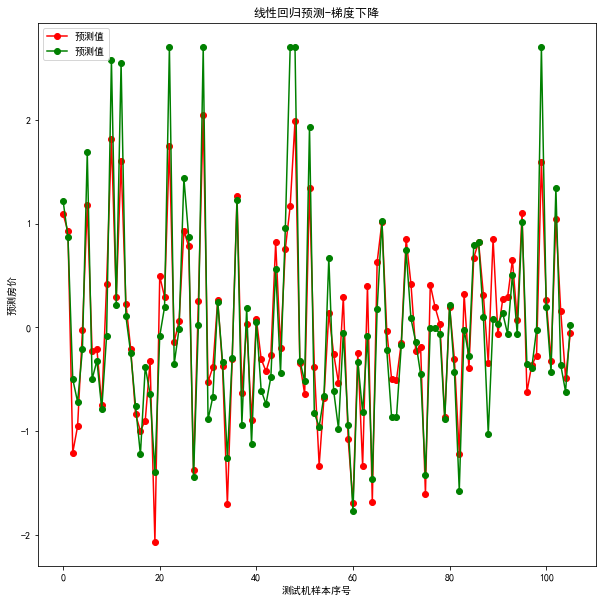
    1. plt.figure(figsize=(10,10))
    2. plt.plot(result, "ro-", label="预测值")
    3. plt.plot(test_y.values, "go-", label="预测值") # pandas读取时serise类型，我们需要转为ndarray
    4. plt.title("线性回归预测-梯度下降")
    5. plt.xlabel("测试机样本序号")
    6. plt.ylabel("预测房价")
    7. plt.legend()
    8. plt.show()

    image.png

    1. # 绘制累计误差值
    2. plt.plot(range(1,lr.times+1),lr.loss_, "o-")

    image.png

    1. # 因为放假更新涉及多个维度，不方便可视化
    2. # 为了可视化，我们只选择其中一个维度（RM），并画出直线，进行拟合
    3. lr = LinearRegression(learning_rate=0.0005, times=20)
    4. t = data.sample(len(data), random_state=0)
    5. train_X = t.iloc[:400, 6:7]
    6. train_y = t.iloc[:400, -1]
    7. test_X = t.iloc[400:, 5:6]
    8. test_y = t.iloc[400:, -1]
    9. # 标准化
    10. ss = StandardScaler()
    11. train_X = ss.fit_transform(train_X)
    12. test_X = ss.fit_transform(test_X)
    13. ss2 = StandardScaler()
    14. train_y = ss2.fit_transform(train_y)
    15. test_y = ss2.fit_transform(test_y)
    16. lr.fit(train_X, train_y)
    17. result = lr.predict(test_X)
    18. # display(result)
    19. display(np.mean((result - test_y)**2))

    2.002805351917207

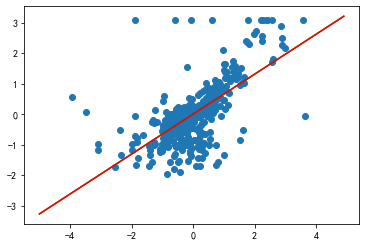
    1. # 展示rm对对于价格的影响
    2. plt.scatter(train_X["rm"], train_y)
    3. # 展示权重
    4. display(lr.w_)
    5. # 构建方程 y = w0 + x*w1 = -3.05755421e-16 + x *  6.54993957e-01
    6. x = np.arange(-5,5,0.1)
    7. y = -3.05755421e-16 + x *  6.54993957e-01
    8. plt.plot(x, y, "g") # 绿色直线显示我们的拟合直线
    9. # *********  x.reshape(-1,1) 把一维转为二位 ****************
    10. plt.plot(x, lr.predict(x.reshape(-1,1)), 'r')
    12. # 可以看到我们预测的和你和的完全重合了

    array([-3.05755421e-16, 6.54993957e-01])
    image.png