• 数据介绍

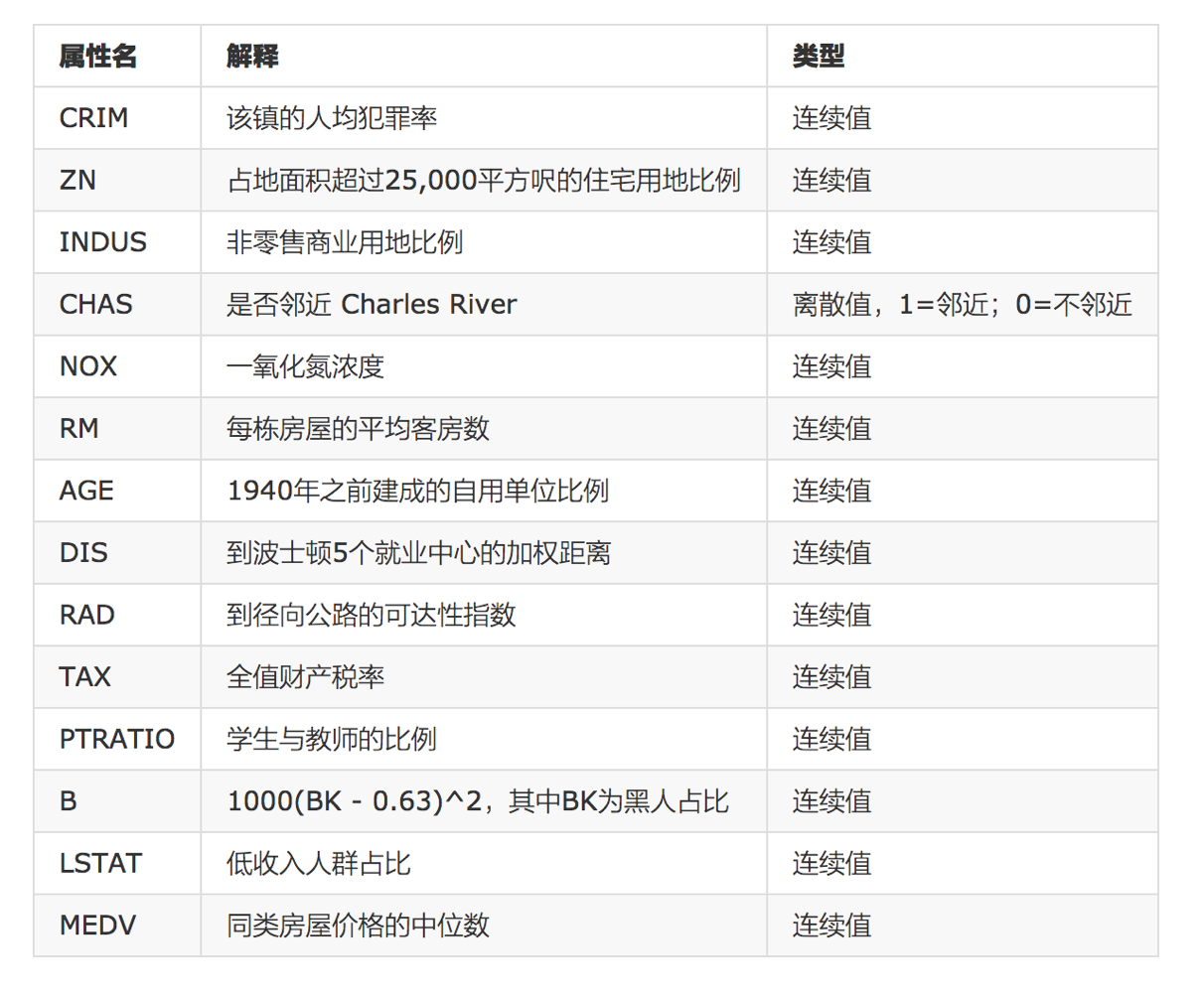
  给定的这些特征，是专家们得出的影响房价的结果属性。我们此阶段不需要自己去探究特征是否有用，只需要使用这些特征。到后面量化很多特征需要我们自己去寻找

1 分析

回归当中的数据大小不一致，是否会导致结果影响较大。所以需要做标准化处理。

• 数据分割与标准化处理
• 回归预测

• 线性回归的算法效果评估

  2 回归性能评估

  均方误差(Mean Squared Error)MSE)评价机制：
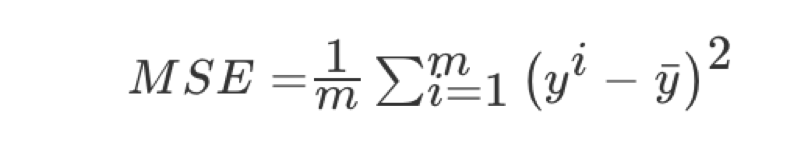
  注：yi为预测值，¯y为真实值

• sklearn.metrics.mean_squared_error(y_true, y_pred)

  • 均方误差回归损失
  • y_true:真实值
  • y_pred:预测值

  • return:浮点数结果

    3 代码

    ```python def linear_model1(): “”” 线性回归:正规方程 :return:None “””

    1.获取数据

    data = load_boston()

    2.数据集划分

    x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22)

    3.特征工程-标准化

    transfer = StandardScaler() x_train = transfer.fit_transform(x_train) x_test = transfer.fit_transform(x_test)

    4.机器学习-线性回归(特征方程)

    estimator = LinearRegression() estimator.fit(x_train, y_train)

    5.模型评估

    5.1 获取系数等值

    ypredict = estimator.predict(x_test) print(“预测值为:\n”, y_predict) print(“模型中的系数为:\n”, estimator.coef) print(“模型中的偏置为:\n”, estimator.intercept_)

    5.2 评价

    均方误差

    error = mean_squared_error(y_test, y_predict) print(“误差为:\n”, error)

def linear_model2(): “”” 线性回归:梯度下降法 :return:None “””

# 1.获取数据
data = load_boston()
# 2.数据集划分
x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22)
# 3.特征工程-标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.fit_transform(x_test)
# 4.机器学习-线性回归(特征方程)
estimator = SGDRegressor(max_iter=1000)
estimator.fit(x_train, y_train)
# 5.模型评估
# 5.1 获取系数等值
y_predict = estimator.predict(x_test)
print("预测值为:\n", y_predict)
print("模型中的系数为:\n", estimator.coef_)
print("模型中的偏置为:\n", estimator.intercept_)
# 5.2 评价
# 均方误差
error = mean_squared_error(y_test, y_predict)
print("误差为:\n", error)

我们也可以尝试去修改学习率
```python
estimator = SGDRegressor(max_iter=1000,learning_rate="constant",eta0=0.1)

此时我们可以通过调参数，找到学习率效果更好的值。