C2W2 Quiz - Optimization algorithms

image.png
Ans: C
Note: [i]{j}(k) superscript means i-th layer, j-th minibatch, k-th example

image.png
Ans: A
Note: Vectorization is not for computing several mini-batches in the same time.

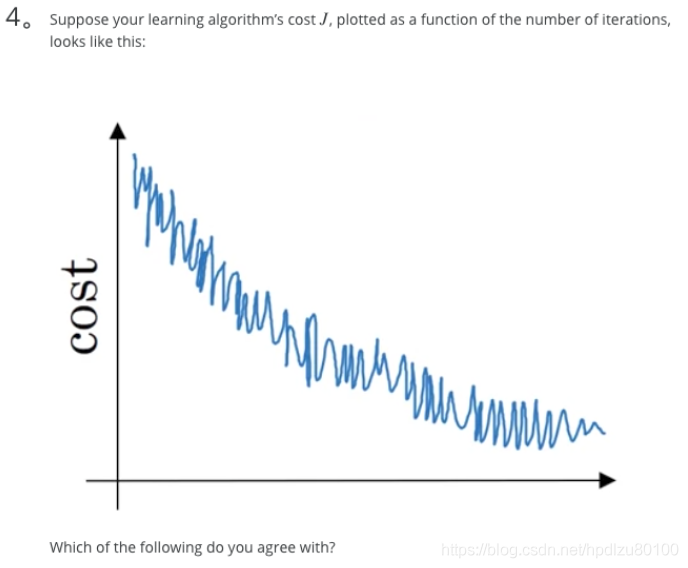
image.png
Ans: B、C
image.png
image.png
Ans : D
image.png
Ans: A
image.png
Ans: B
Note: This will explode the learning rate rather than decay it.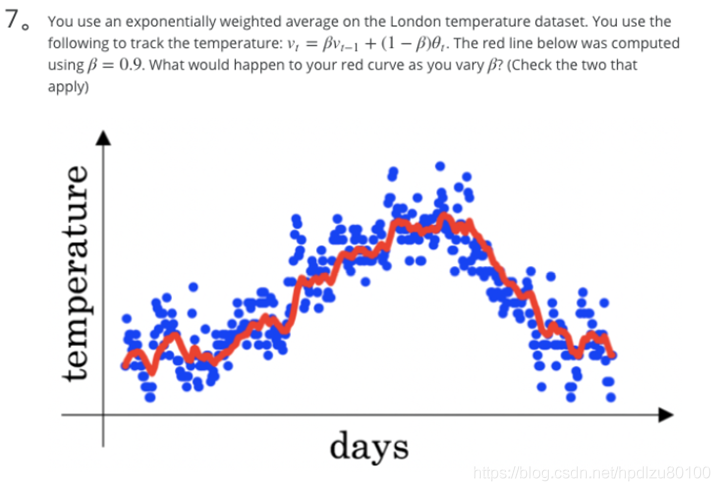
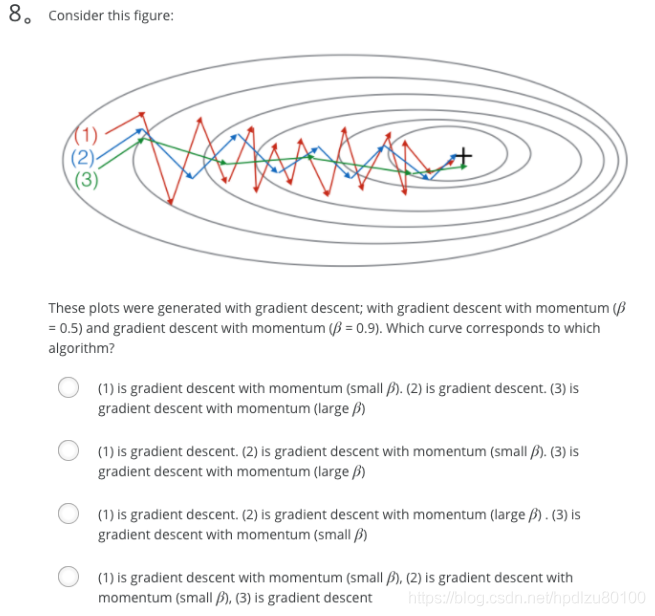
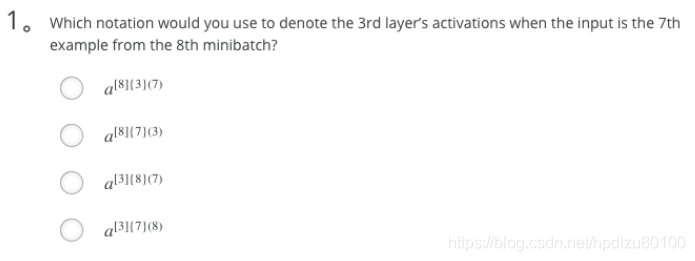
image.png
image.png
Ans: B、C
image.png
Ans: B
image.png
Ans: A、C、D、E
image.png
Ans: B

  1. Which notation would you use to denote the 3rd layer’s activations when the input is the 7th example from the 8th minibatch?
  • a^[3]{8}(7)

Note: [i]{j}(k) superscript means i-th layer, j-th minibatch, k-th example

  1. Which of these statements about mini-batch gradient descent do you agree with?
  • You should implement mini-batch gradient descent without an explicit for-loop over different mini-batches, so that the algorithm processes all mini-batches at the same time (vectorization).
  • Training one epoch (one pass through the training set) using mini-batch gradient descent is faster than training one epoch using batch gradient descent.
  • One iteration of mini-batch gradient descent (computing on a single mini-batch) is faster than one iteration of batch gradient descent.

Note: Vectorization is not for computing several mini-batches in the same time.

  1. Why is the best mini-batch size usually not 1 and not m, but instead something in-between?
  • If the mini-batch size is 1, you lose the benefits of vectorization across examples in the mini-batch.
  • If the mini-batch size is m, you end up with batch gradient descent, which has to process the whole training set before making progress.
  1. Suppose your learning algorithm’s cost J, plotted as a function of the number of iterations, looks like this:
  • If you’re using mini-batch gradient descent, this looks acceptable. But if you’re using batch gradient descent, something is wrong.

Note: There will be some oscillations when you’re using mini-batch gradient descent since there could be some noisy data example in batches. However batch gradient descent always guarantees a lower J before reaching the optimal.

  1. Suppose the temperature in Casablanca over the first three days of January are the same:
    Jan 1st: θ_1 = 10
    Jan 2nd: θ_2 = 10
    Say you use an exponentially weighted average with β = 0.5 to track the temperature: v_0 = 0, v_t = βv_t−1 + (1 − β)θ_t. If v_2 is the value computed after day 2 without bias correction, and v^corrected_2 is the value you compute with bias correction. What are these values?

v_2 = 7.5, v^corrected_2 = 10

  1. Which of these is NOT a good learning rate decay scheme? Here, t is the epoch number.
  • α = e^t * α_0

Note: This will explode the learning rate rather than decay it.

  1. You use an exponentially weighted average on the London temperature dataset. You use the following to track the temperature: v_t = βv_t−1 + (1 − β)θ_t. The red line below was computed using β = 0.9. What would happen to your red curve as you vary β? (Check the two that apply)
  • Increasing β will shift the red line slightly to the right.
  • Decreasing β will create more oscillation within the red line.

  1. Consider this figure:
    These plots were generated with gradient descent; with gradient descent with momentum (β = 0.5) and gradient descent with momentum (β = 0.9). Which curve corresponds to which algorithm?
    (1) is gradient descent. (2) is gradient descent with momentum (small β). (3) is gradient descent with momentum (large β)

  2. Suppose batch gradient descent in a deep network is taking excessively long to find a value of the parameters that achieves a small value for the cost function J(W[1],b[1],…,W[L],b[L]). Which of the following techniques could help find parameter values that attain a small value forJ? (Check all that apply)

  • Try using Adam
  • Try better random initialization for the weights
  • Try tuning the learning rate α
  • Try mini-batch gradient descent
  • Try initializing all the weights to zero
  1. Which of the following statements about Adam is False?
  • Adam should be used with batch gradient computations, not with mini-batches.

Note: Adam could be used with both.