1.1 Mini-batch 梯度下降法

Mini-batch是指将大的数据集分成更小规模的子集
image.png
采用mini-batch梯度下降，在每次遍历完一个mini-batch后即可更新参数，而不用等待遍历完全部训练集才更新参数
image.png

1.2 理解 mini-batch 梯度下降法

Mini-batch梯度下降不如Batch梯度下降那么平滑，但是整体趋势还是下降的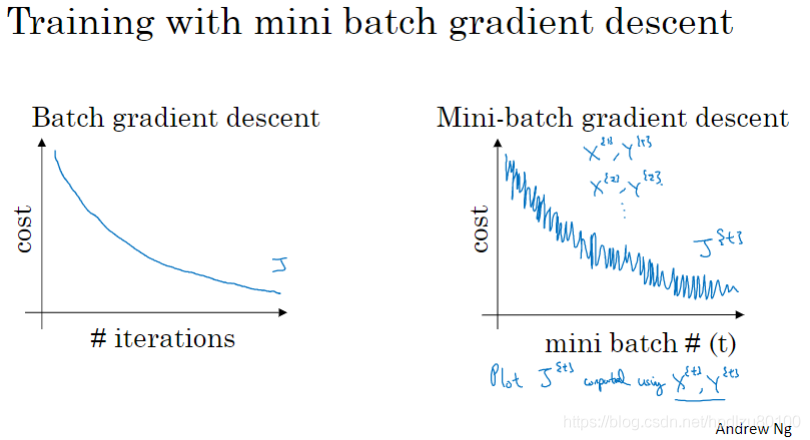
image.png
选择mini-batch的大小：
当size = m时，即为普通的batch梯度下降
当size = 1时，即为随机（stochastic）梯度下降
通常，选择折中的大小，mini-batch的大小也可作为一个超参数（hyper-parameter）进行确定
image.png
Mini-batch的大小通常选择为2的整数次幂（否则，训练速度可能会断崖式下降）
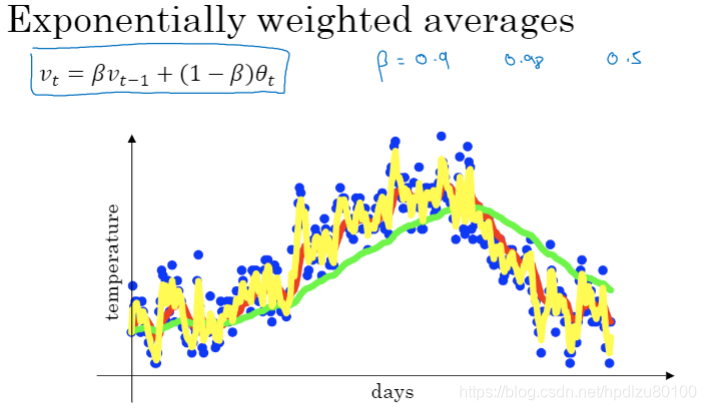
image.png

1.3 指数加权平均

通过加权平均，可以让数据更加“平滑”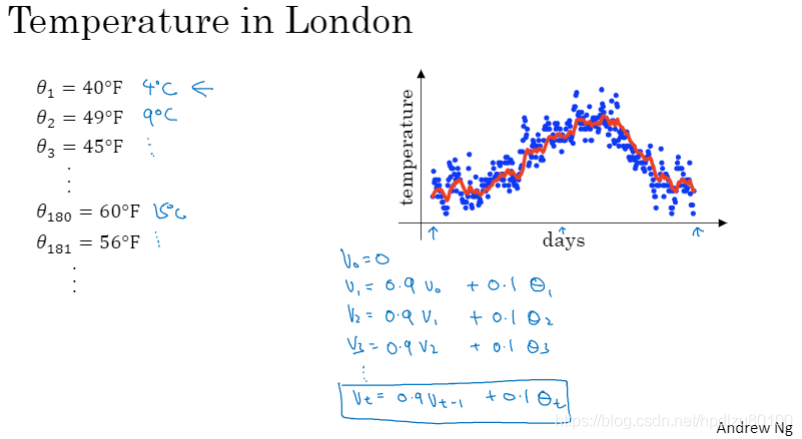
image.png
指数加权平均（vt = βvt-1 + (1-β)θt），β值越高，数据曲线更平滑，但同时曲线会更加向右偏移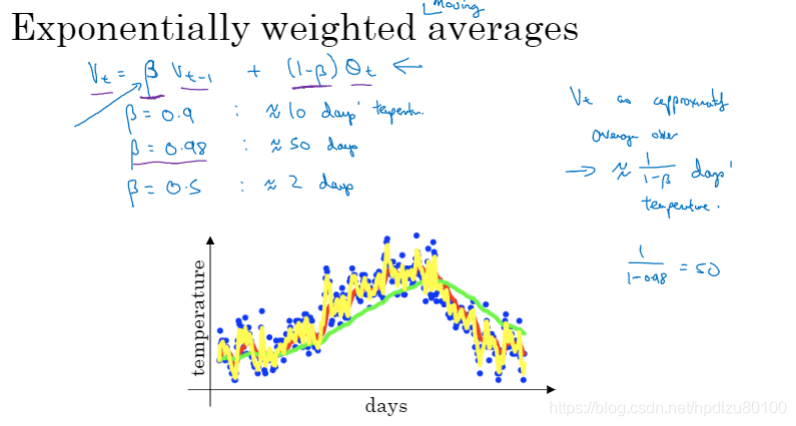
image.png

1.4 理解指数加权平均

image.png
指数加权平均中的β有什么含义？β值越高，相当于在计算新值（当前值）时考虑了更多的历史数据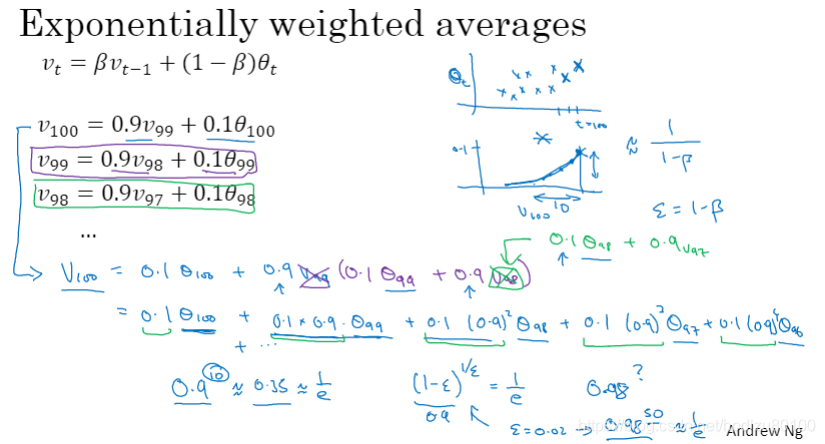
image.png
指数加权平均的实现示例，其优点是占用内存小（只用一行代码表示旧值）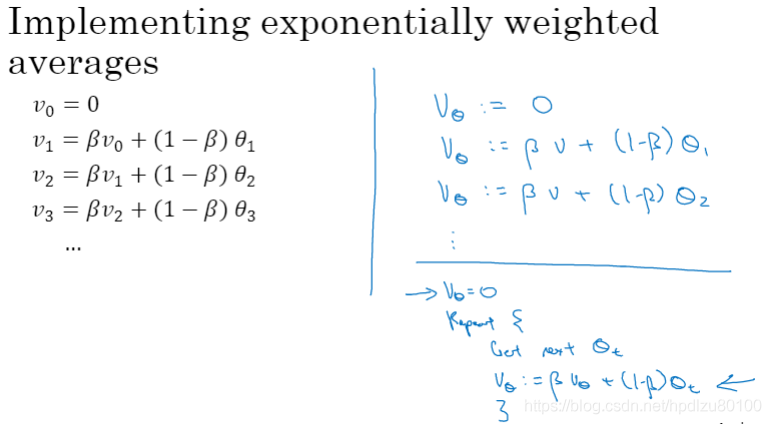
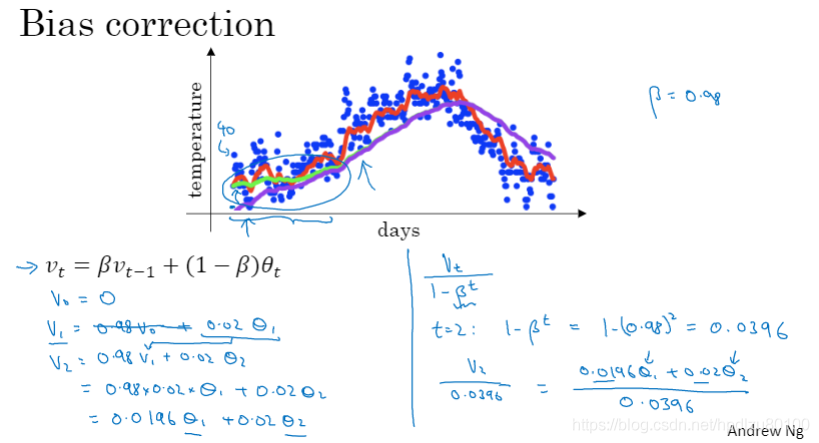
image.png

1.5 指数加权平均的偏差修正

采用指数加权平均后，头部数据值会明显偏低（出现偏差），可对此进行修正
image.png