1 Bagging集成原理

目标：把下面的圈和方块进行分类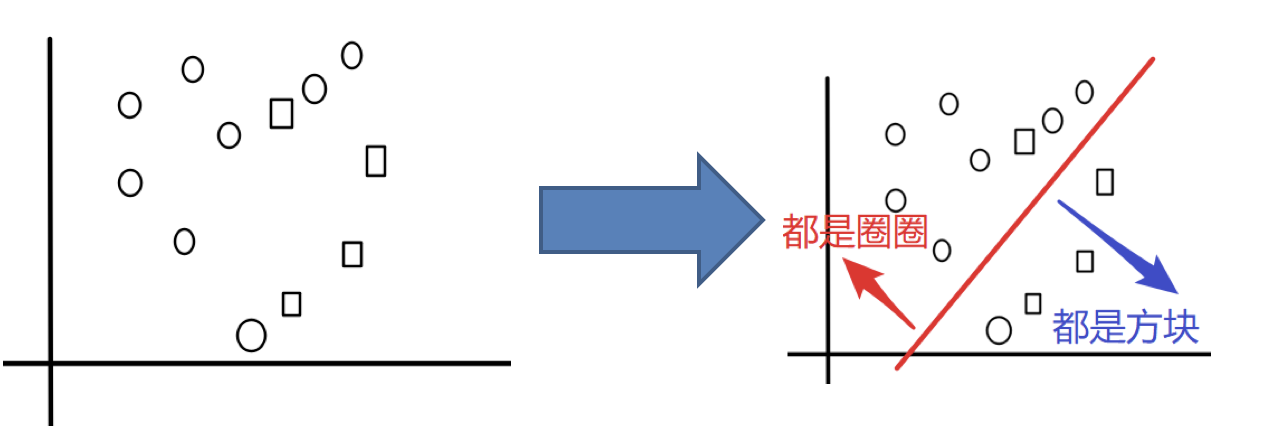bagging1.png
实现过程：
1.采样不同数据集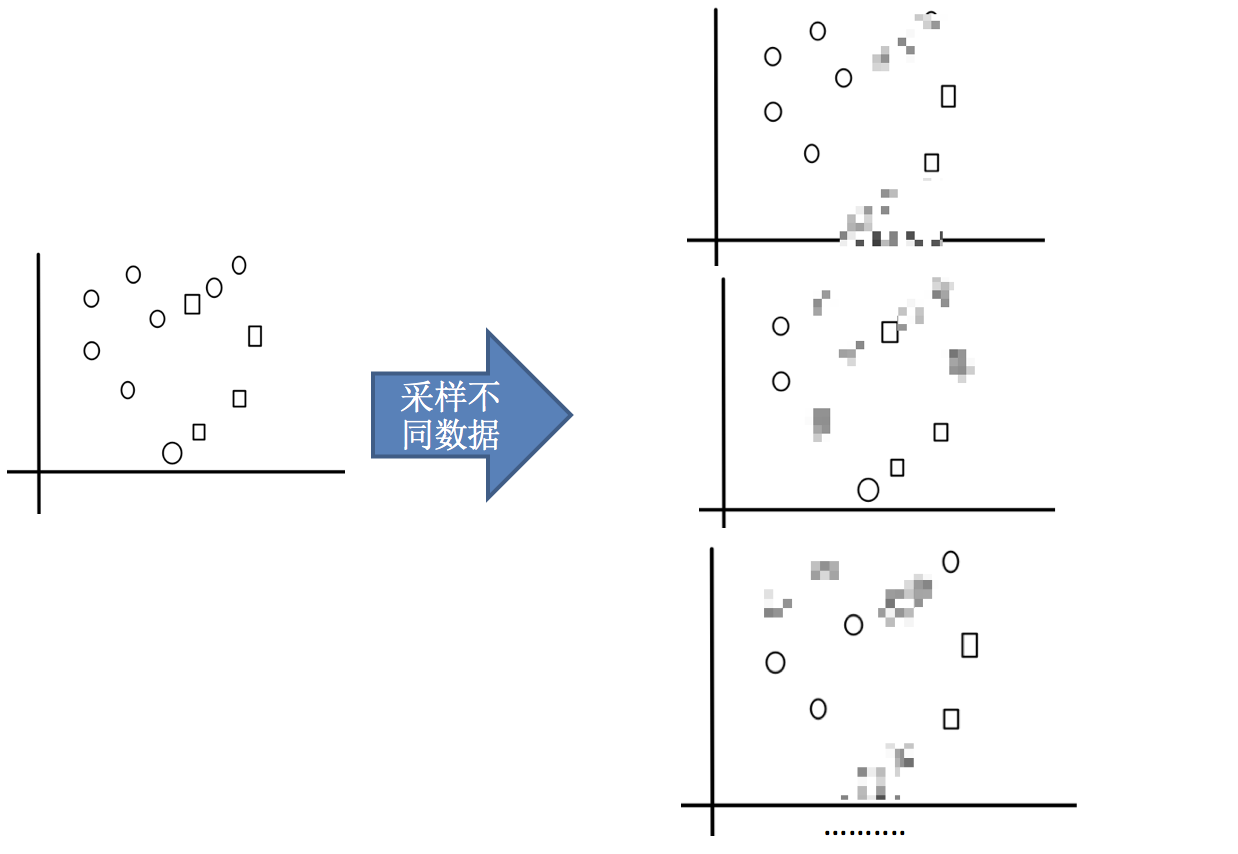bagging2.png
2.训练分类器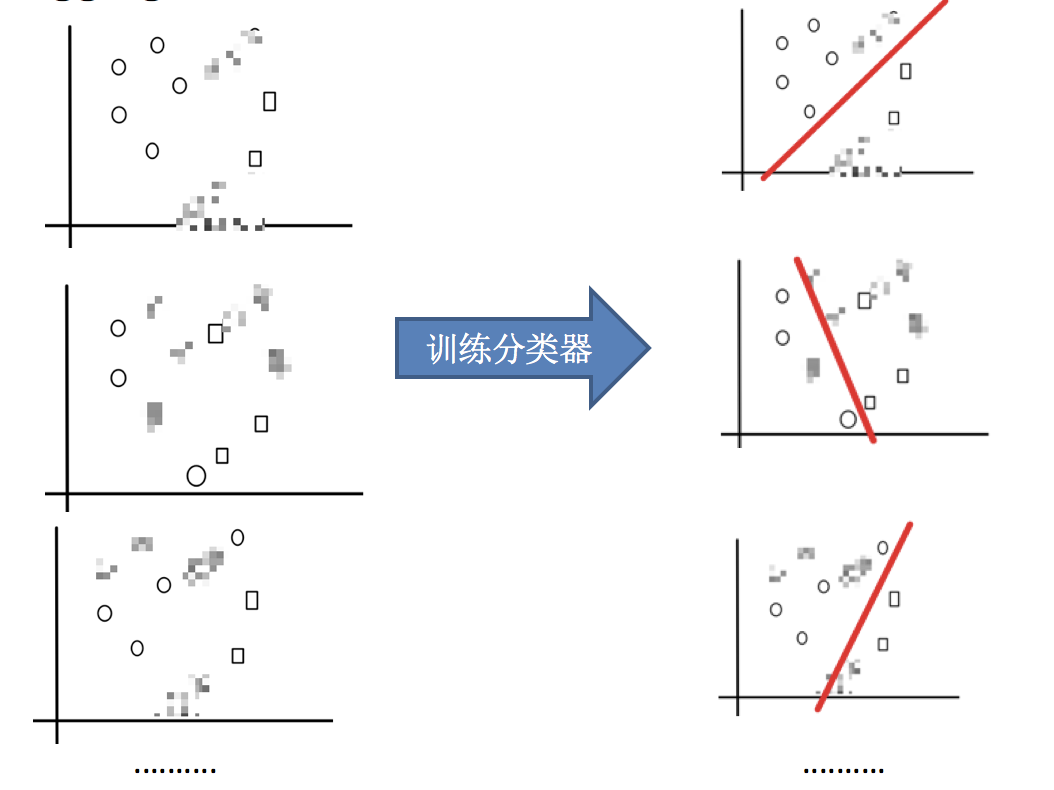bagging3.png
3.平权投票，获取最终结果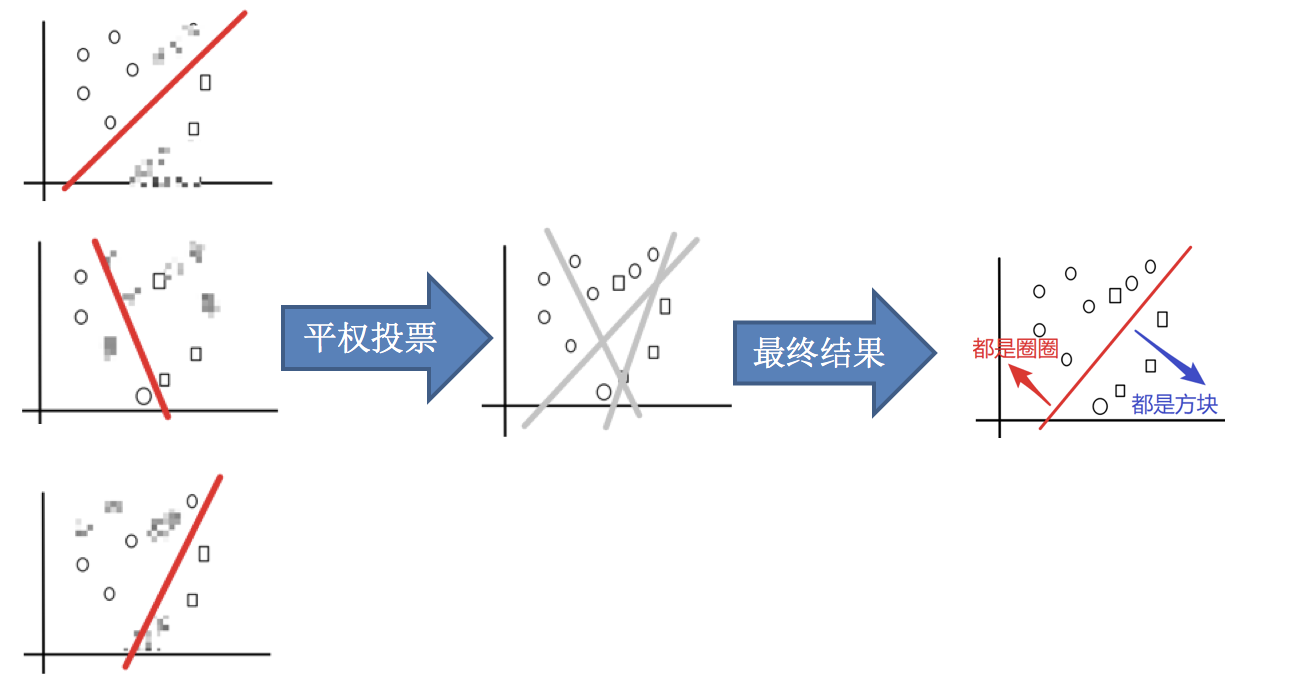bagging4.png
4.主要实现过程小结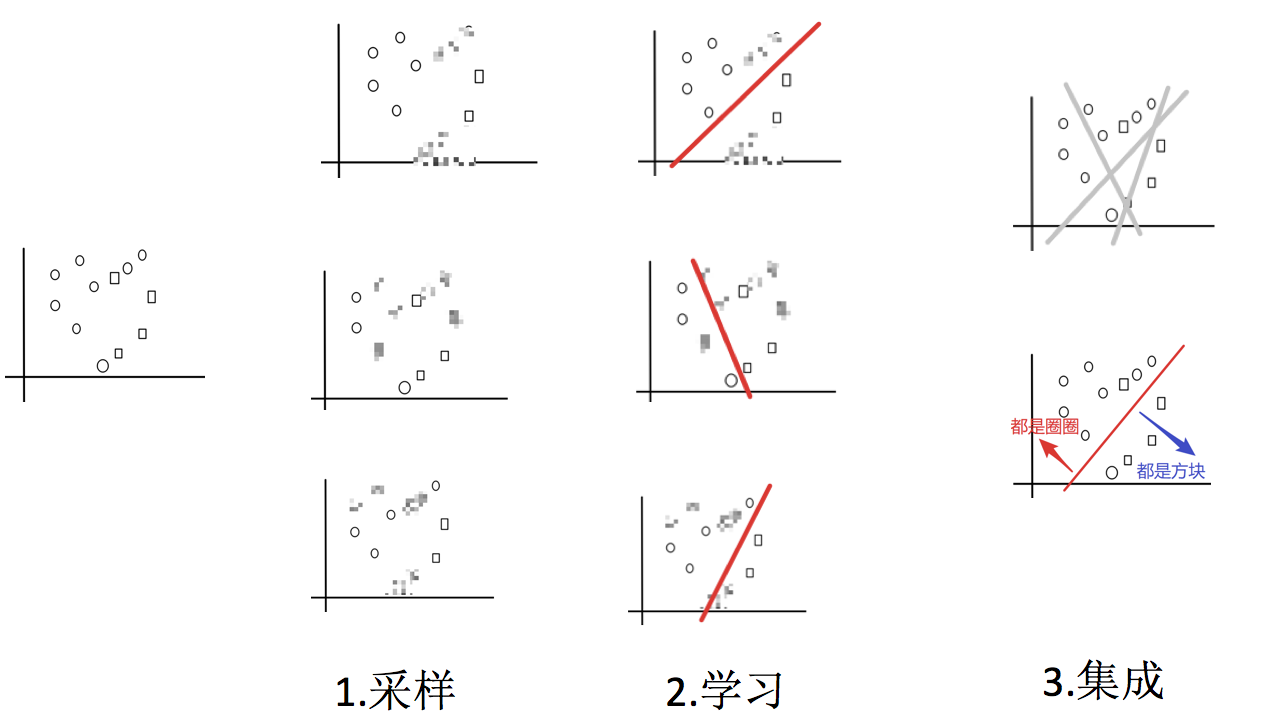bagging5.png

2 随机森林构造过程

在机器学习中，随机森林是一个包含多个决策树的分类器，并且其输出的类别是由个别树输出的类别的众数而定。
随机森林 = Bagging + 决策树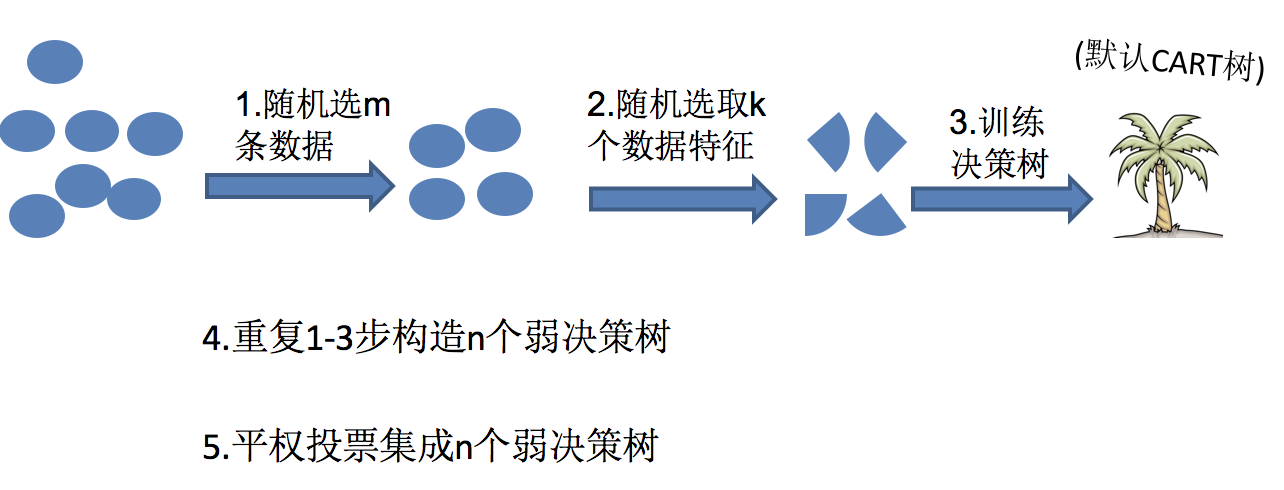tf1.png
例如, 如果你训练了5个树, 其中有4个树的结果是True, 1个树的结果是False, 那么最终投票结果就是True

随机森林够造过程中的关键步骤（用N来表示训练用例（样本）的个数，M表示特征数目）：
1）一次随机选出一个样本，有放回的抽样，重复N次（有可能出现重复的样本）
2） 随机去选出m个特征, m <<M，建立决策树

  • 思考

    • 1.为什么要随机抽样训练集？ 如果不进行随机抽样，每棵树的训练集都一样，那么最终训练出的树分类结果也是完全一样的
    • 2.为什么要有放回地抽样？如果不是有放回的抽样，那么每棵树的训练样本都是不同的，都是没有交集的，这样每棵树都是“有偏的”，都是绝对“片面的”（当然这样说可能不对），也就是说每棵树训练出来都是有很大的差异的；而随机森林最后分类取决于多棵树（弱分类器）的投票表决。

      3 随机森林api介绍

  • sklearn.ensemble.RandomForestClassifier(n_estimators=10, criterion=’gini’, max_depth=None, bootstrap=True, random_state=None, min_samples_split=2)

    • n_estimators：integer，optional（default = 10）森林里的树木数量120,200,300,500,800,1200
    • Criterion：string，可选（default =“gini”）分割特征的测量方法
    • max_depth：integer或None，可选（默认=无）树的最大深度 5,8,15,25,30
    • max_features=”auto”,每个决策树的最大特征数量
      • If “auto”, then max_features=sqrt(n_features).
      • If “sqrt”, then max_features=sqrt(n_features)(same as “auto”).
      • If “log2”, then max_features=log2(n_features).
      • If None, then max_features=n_features.
    • bootstrap：boolean，optional（default = True）是否在构建树时使用放回抽样
    • min_samples_split:节点划分最少样本数
    • min_samples_leaf:叶子节点的最小样本数

  • 超参数：n_estimator, max_depth, min_samples_split,min_samples_leaf

    4 随机森林预测案例

  • 实例化随机森林

    1. # 随机森林去进行预测
    2. rf = RandomForestClassifier()

  • 定义超参数的选择列表

    1. param = {"n_estimators": [120,200,300,500,800,1200], "max_depth": [5, 8, 15, 25, 30]}

  • 使用GridSearchCV进行网格搜索 ```python

    超参数调优

    gc = GridSearchCV(rf, param_grid=param, cv=2)

gc.fit(x_train, y_train)

print(“随机森林预测的准确率为：”, gc.score(x_test, y_test)) ```

注意

  • 随机森林的建立过程
  • 树的深度、树的个数等需要进行超参数调优

5 bagging集成优点

Bagging + 决策树/线性回归/逻辑回归/深度学习… = bagging集成学习方法
经过上面方式组成的集成学习方法:

  1. 均可在原有算法上提高约2%左右的泛化正确率
  2. 简单, 方便, 通用