3.6.2 法截线

法截线【一般】

在平面上，最重要的线元素是直线，参考椭球面上的线元素全为曲线，其中最重要的参考椭球面曲线元素是法截线。

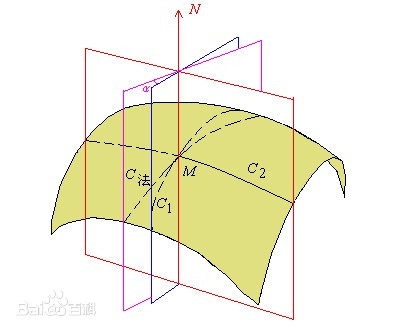
法截面

包含过椭球面上任意一点的法线P的平面叫法截面。

一条法线可以生成无数个法截面。

法截线

法截面与椭球面的交线叫做法截线。

法截弧

法截线的分段叫法截弧。

参考椭球面上同一点上，不同方向的法截弧的曲率半径一般都不相同。

主法截线【选读】

• 子午圈与赤道面相垂直的大圆。
• 卯酉圈与子午圈相垂直的法截圈。卯酉圈是与P点处子午面垂直的法截面EPE′与椭球的交线，它的曲率中心n正好位于椭球的旋转轴OO′上。

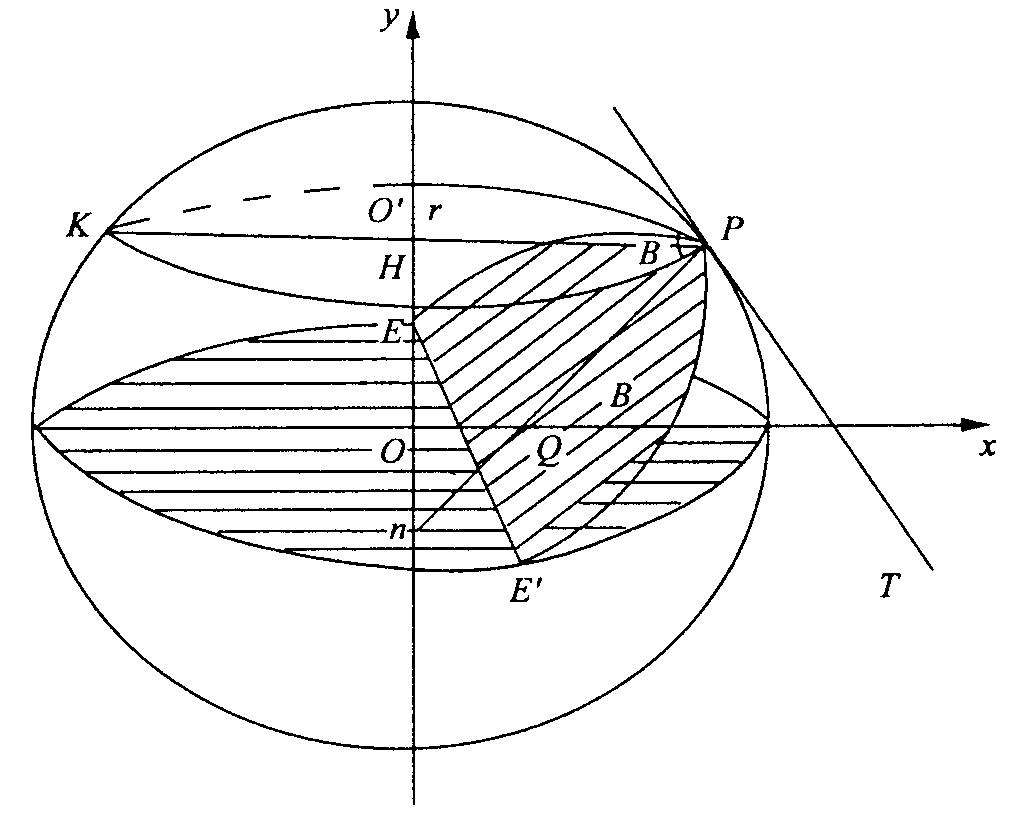
子午法截弧为参考椭球面上南北方向，大地方位角为0°或180°，卯酉法截弧为参考椭球面上东西方向，大地方位角为90°或270°，两者正交。
假设人站在参考椭球面上面向北极点，则人站立方向为法线方向，子午圈方向即南北方向，卯酉圈方向为东西方向，子午面和卯酉面都包含人的站立线。

曲率半径【选读】

• 子午圈上的曲率半径

子午圈的曲率半径在赤道上小于赤道半径，随着纬度的增大而增大，在极点上等于极曲率半径。

• 卯酉圈上的曲率半径

当纬度为0°时卯酉圈就等于赤道，随着纬度的增加，卯酉圈的曲率半径增大，纬度为90°时等于极曲率半径。

• 椭球上任意方向法截弧曲率半径

任意方向法截弧曲率半径的极小值即子午圈曲率半径，极大值即卯酉圈曲率半径，故子午圈曲率半径和卯酉圈曲率半径称为主曲率半径。
曲面上任意点的平均曲率半径是该点上主曲率半径的几何平均值。

主曲率半径和任意方向法截弧曲率半径计算公式：【扩展】 其中

式中 R——任意方向平均曲率半径； M——子午圈曲率半径； N——卯酉圈曲率半径； c——极曲率半径； a——长半轴； b——短半轴； e——偏心率； B——所在纬度。