2.1.5 偶然误差

2.1.5.1 偶然误差规律

相同观测条件下，对同一标的进行多次测量，所得观测值的偶然误差的分布符合正态分布曲线特点。
一定的观测条件下的（即等精度）若干观测值，对应一种确定的误差正态分布曲线。

正态分布曲线较陡峭，表示一组等精度观测值的观测条件较好，误差聚集分布于较小的值域区间内，故整体上误差较小，精度较高；反之，表示观测条件较差，精度较低，误差分布离散。

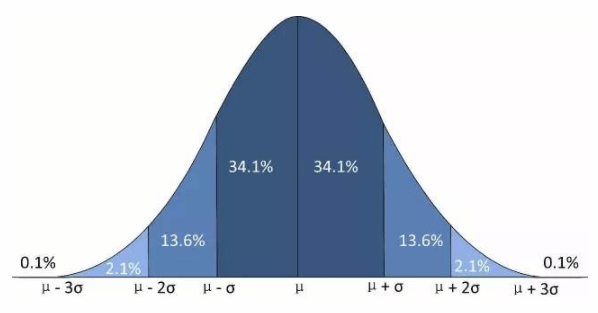
误差曲线

在偶然误差直方图中，用横坐标表示真误差大小，用纵坐标表示误差在一定区间内出现的频率。

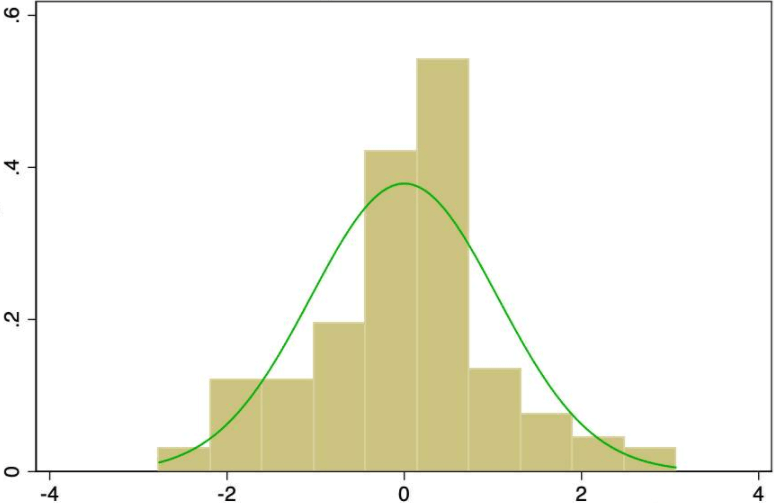
误差直方图

2.1.5.2 偶然误差分布特性

偶然误差的分布呈现有限性、渐降性、对称性、抵偿性四个特征。

• 有限性：一定观测条件下，误差的绝对值有一定限值。
• 渐降性：绝对值较小的误差比绝对值较大的误差出现的概率大。
• 对称性：绝对值相等的正负误差出现的概率相同。
• 抵偿性：偶然误差的数学期望（随机变量可能取值的理论平均值）为零，即当观测次数无限多时，误差平均值无限接近于零。