1. 计算校验位数
要使用海明码纠错,首先就要确定发送的数据所需要要的校验码(也就是“海明码”)位数(也称“校验码长度”)。它是这样的规定的:假设用N表示添加了校验码位后整个信息的二进制位数,用K代表其中有**效信息位数**,r表示添加的**校验码位**,它们之间的关系应满足:**N=K+r≤2r-1**。
计算公式:2^r>=K+r+1
举例:求信息1011的海明码。
| 信息码位数 | 1 | 2~4 | 5~11 | 12~26 | 27~57 | 58~120 | 121~247 |
|---|---|---|---|---|---|---|---|
| 校验码位数 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
1011有4位那么R=3,即2^3>=4+3+1.
求1010110为例进行海明码编码。
1010110有7位那么R=4,即2^4>=7+4+1.
2.确定校验码位置
校验码不是直接附加在信息码的前面、后面或中间的,而是分开插入到不同的位置。
校验码必须是在2n次方位置,如第1、2、4、8、16、32,……位(对应20、21、22、23、24、25,……,是从最左边的位数起的),这样一来就知道了信息码的分布位置,也就是非2n次方位置,如第3、5、6、7、9、10、11、12、13,……位(是从最左边的位数起的)。
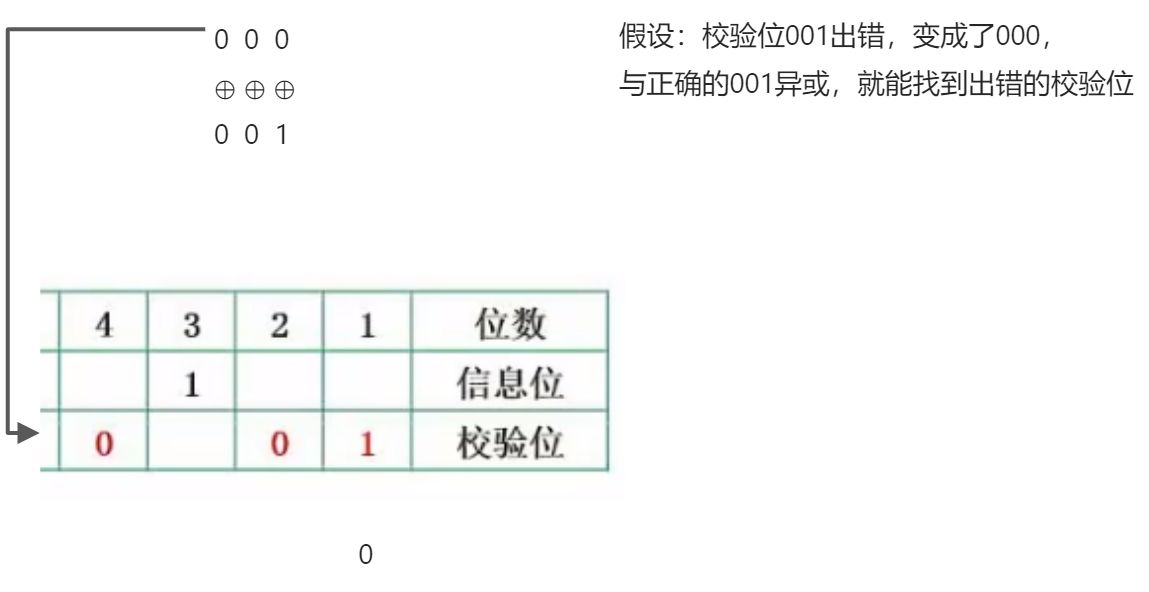
比如:1011 1010
| 位数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 信息位 | 1 | 1 | 1 | 0 | ||||
| 校验位 | 0 | 1 | 0 | 1 |
3. 确定校验码
即便确定了所需的校验码位数和这些校验码的插入位置,但这还不够,还得确定各个校验码值。
只能采用奇校验,还是偶校验来确定。
1)计算方法
我们把整个校验位与编码位用图说话: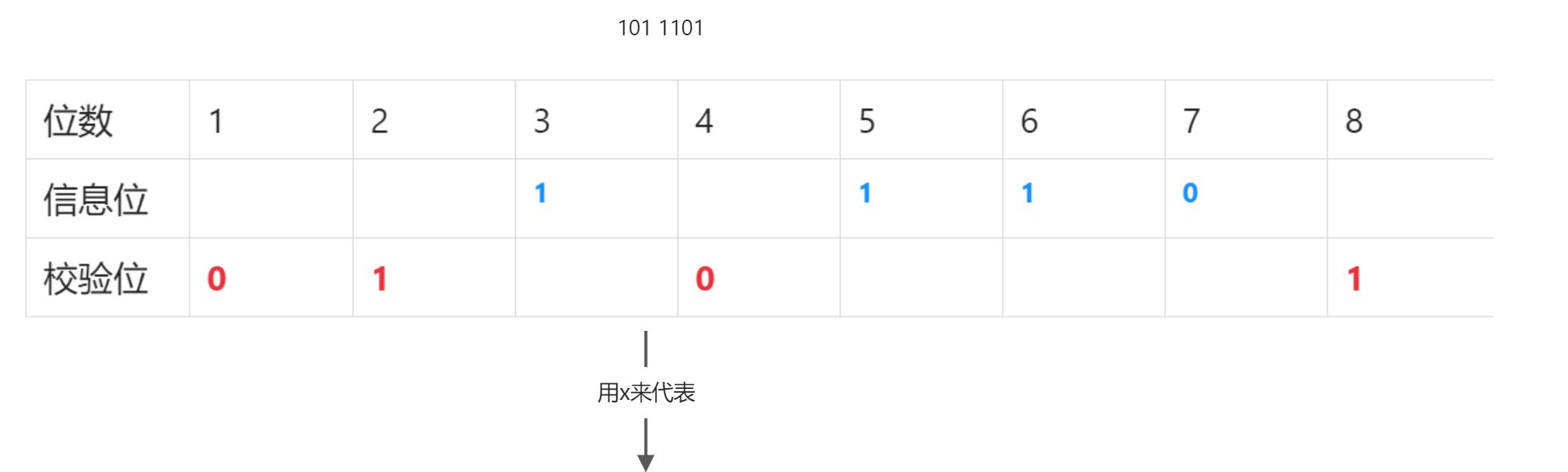
将图竖过来,其实就是2^n,2^0、2^1、2^2、2^3…(在不同的校验位上,以2^n在位数上校验,用奇校验或偶校验)
| 位数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 校验位 | x1→p1 | X | X | X | X | X | X | ||||||
| x2→p2 | X | X | X | X | X | X | |||||||
| x3→p4 | X | X | X | X | |||||||||
| x4→p8 | X | X | X | X | |||||||||
| x5→p16 |
以1011 1010 为例:
将其位数转换为二进制:
| 位数 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 信息位 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | ||||
| 校验位 | x1 | x2 | x3 | x4 |
然后按照p1(x1)、p2(x2)、p3(x3)、p4(x4)异或计算:
异或的运算规则:
0^0=0; 0^1=1; 1^0=1; 1^1=0;
首先计算p1:
将位数对应栏的所有最后一位为1(xxx1格式)相异或为0,即:
| 位数 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 信息位 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | ||||
| 校验位 | x1 | x2 | x3 | x4 |
拿到所有的信息位,进行异或操作:
x1^1^0^1^1^1 = 0
则 x1= 0;
接着计算x2,同样的道理,取出位数的对应栏的所有倒数第二位为1(xx1x格式)相异或为0,即:
| 位数 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 信息位 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | ||||
| 校验位 | x1 | x2 | x3 | x4 |
x2^1^0 = 0
则 x2 = 1;
以此类推,其实就是2^n校验位。
x3^0^1^1=0,x3 =0
x4^1^0^1^0=0,x4 = 0
最终结果:011001101010(海明码)
4. 海明码校验