矩阵的建立

1. 直接输入矩阵

>> A = [1,2,3;4,5,6;7,8,9]
A =
     1     2     3
     4     5     6
     7     8     9

1. 利用已有矩阵建立

   >> A = [1,2,3;4,5,6;7,8,9];
   >> B = [-1,-2,-3;-4,-5,-6;-7,-8,-9];
   >> C = [A,B;B,A]
   C =
     1     2     3    -1    -2    -3
     4     5     6    -4    -5    -6
     7     8     9    -7    -8    -9
    -1    -2    -3     1     2     3
    -4    -5    -6     4     5     6
    -7    -8    -9     7     8     9

2. 可以用实部矩阵和虚部矩阵构成复数矩阵

   >> B = [1,2,3;4,5,6];
   >> C = [6,7,8;9,10,11];
   >> A = B + i*C
   A =
   1.0000 + 6.0000i   2.0000 + 7.0000i   3.0000 + 8.0000i
   4.0000 + 9.0000i   5.0000 +10.0000i   6.0000 +11.0000i

3. 冒号表达式

等价于 linspace 函数

• 这里面的 linspace 函数包含头和尾元素

  >> x = linspace(0,pi,6)
  x =
         0    0.6283    1.2566    1.8850    2.5133    3.1416

  结构矩阵和单元矩阵

1. 结构矩阵

>> a(1).x1 = 10;
>> a(1).x2 = 'liu';
>> a(1).x3 = [11,21;34,78];
>> a(2).x1=12;
>> a(2).x2='wang';
>> a(3).x3=[34,191;27,578];

1. 单元矩阵

>> b = {10, 'liu', [11,21;34,78]; 12,'wang',[34,191;27,578]}
b =
  2×3 cell 数组
    {[10]}    {'liu' }    {2×2 double}
    {[12]}    {'wang'}    {2×2 double}

矩阵操作

矩阵元素的引用方式

1. 通过下标

   1. MATLAB中下标从1开始

      >> A(3,2) = 200

      

      >> A = [1,2,3;4,5,6];
      >> A(4,5) = 10
      A =
      1     2     3     0     0
      4     5     6     0     0
      0     0     0     0     0
      0     0     0     0    10

2. 通过序号来引用

>> A = [1,2,3;4,5,6]
A =
     1     2     3
     4     5     6
>> A(3)
ans =
     2

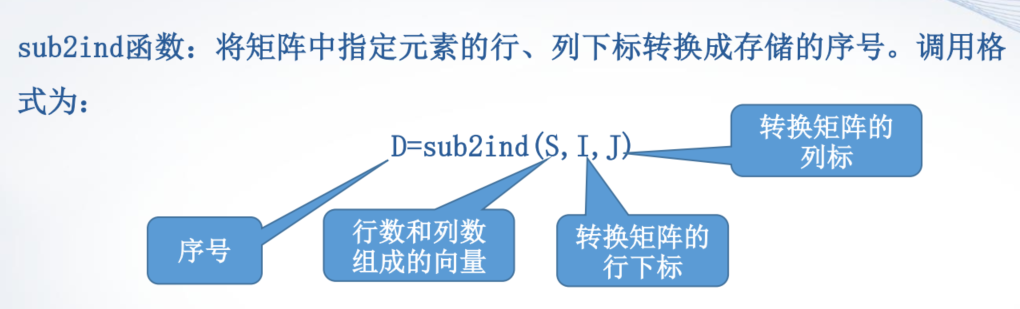
>> A = [1:3;4:6]
A =
     1     2     3
     4     5     6
>> D = sub2ind(size(A), [1,2;2,2], [1,1;3,2])
D =
     1     2
     6     4

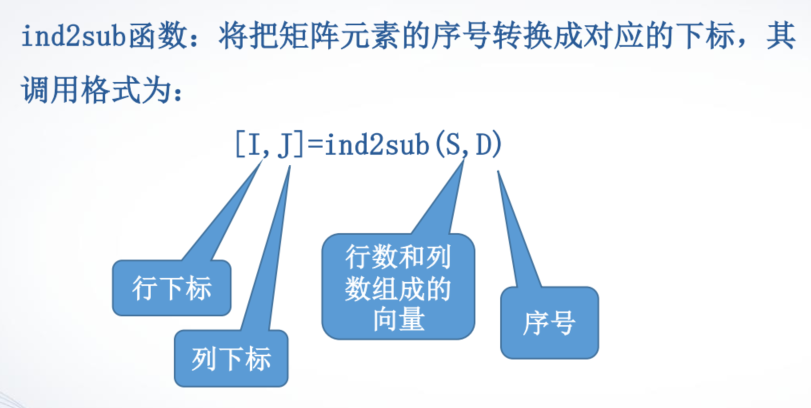
>> [I,J] = ind2sub([3,3], [1,3,5])
I =
     1     3     2
J =
     1     1     2

使用冒号表达式获得子矩阵

>> A = [1,2,3,4,5;6,7,8,9,10;11,12,13,14,15]
A =
     1     2     3     4     5
     6     7     8     9    10
    11    12    13    14    15
>> A(1:2,:)
ans =
     1     2     3     4     5
     6     7     8     9    10
>> A(2:3,1:2:5)
ans =
     6     8    10
    11    13    15

end 运算符：表示某一维的末尾元素下标

利用空元素删除矩阵的元素

>> A = [1,2,3,0,0;7,0,9,2,6;1,4,-1,1,8]
A =
     1     2     3     0     0
     7     0     9     2     6
     1     4    -1     1     8
>> A(:,[2,4]) = []
A =
     1     3     0
     7     9     6
     1    -1     8

该表矩阵的形状

>> x = [23,45,65,34,65,34,33,11,51,23];
>> y = reshape(x, 2, 5)
y =
    23    65    65    33    51
    45    34    34    11    23

A(:) 将矩阵A的每一列元素堆叠起来,成为一个列向量

• 等价于 reshape(A,x,1)

  >> A = [22, 32, 11; 55, 22, 44]
  A =
    22    32    11
    55    22    44
  >> B = A(:)
  B =
    22
    55
    32
    22
    11
    44