有的时候，在二维图像中画出轮廓或者给区域上色，以展示三维数据是很有用的。在 Matplotlib 中有 3 个函数可以帮助我们实现这一功能：

• plt.contour() —- 画出轮廓
• plt.contourf() —- 为轮廓填充颜色
• plt.imshow() —- 展示图像

首先，传统的四连不能忘，但今天的样式变了：

%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('seaborn-white')
import numpy as np

三维函数图像可视化

绘制轮廓图

首先我们从一个简单的函数 开始：

def f(x, y):
    return np.sin(x) ** 10 + np.cos(10 + y * x) * np.cos(x)

使用 plt.contour() 创建一个轮廓图，这个函数需要传入 3 个参数：

• 构成网格中各个点的 x 坐标们
• 构成网格中各个点的 y 坐标们
• 构成网格中各个点的 z 坐标们

  z 值代表图像在点 (x, y) 出的灰度值

处理这种数据最常用的应该就是 np.meshgrid() 函数，它使用 2 个一维数组来建立二维网格：

x = np.linspace(0, 5, 50)
y = np.linspace(0, 5, 40)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)

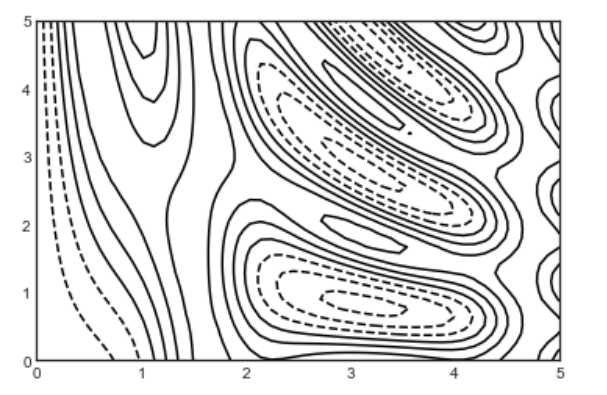
然后我们使用 plt.contour() 画一个只有线条的轮廓图：

plt.contour(X, Y, Z, colors='black')

为轮廓图的曲线着色

注意，如果 colors 指定的是单一的颜色，那么默认情况下 Z 负值在图中使用虚线画出，正值使用实线画出。当然我们也可以通过指定 cmap 参数来给线条着色。下面我们我们将 Z 的取值范围 20 等分，然后进行着色：

plt.contour(X, Y, Z, 20, cmap='RdGy')

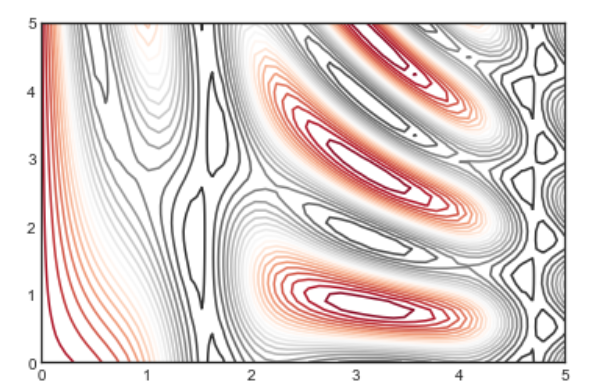
在这里我们使用的是 RdGy ( Red-Gray 的缩写 ) colormap，它能够很好地展示居中的数据。Matplotlib 有很多 colormap 可以使用，你可以通过在 Ipython 中输入 plt.cm 并使用 tab 补全来查看：

plt.cm.<TAB>

为轮廓图填充颜色

但是图中两条线之间的间隙有点误导人，我们可以使用 plt.contourf() 来填充轮廓图中的间隙。 plt.contourf()** 的语法与 plt.contour() 完全一样**。同时，我们还可以使用 plt.colorbar() 来展示颜色条：

plt.contourf(X, Y, Z, 20, cmap='RdGy')
plt.colorbar()

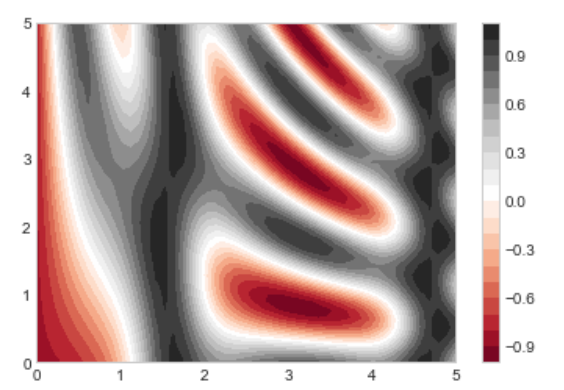
有了颜色条，我们就能很清楚的看到哪里是“山峰”，哪里是“山谷”。

颜色条连续化

还有一个小问题是，颜色条上颜色的步长 ( steps ) 是离散的，而不是连续的，这在有的时候并不是我们想要的。一个解决方法是，我们将 plt.contourf() 的第 4 个参数“Z 值域等分的个数”改的特别高，但这样会使得画图效率特别低。

解决这个问题更好的方式是使用 plt.imshow() 函数，这个函数将二维网格式的数据转换成一张图片。

plt.imshow(Z, extent=[0, 5, 0, 5], origin='lower',
           cmap='RdGy', aspect='equal')
plt.colorbar()

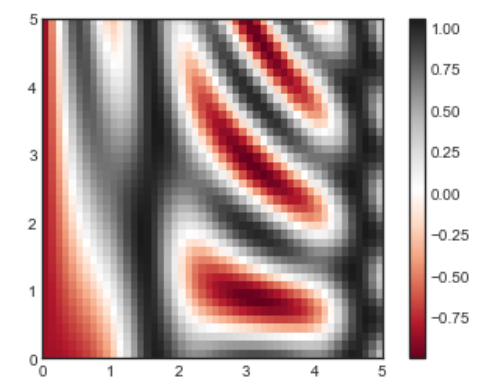
这里有一点 imshow() 小陷阱：

• plt.imshow() 不接受 x 和 y 网格坐标，而是 extent = [xmin, xmax, ymin, ymax]
• plt.imshow() 默认的坐标原点是左上角，所以我们需要使用 origin='lower' 来把原点调整到左下方
• plt.imshow() 的 aspect='equal' 参数是让 x 和 y 轴的单位长度相同

将轮廓图与图像结合

在下面的例子中，我们使用 alpha 改变图像的透明度，使用 plt.clabel() 来指定了轮廓的标签（越来越像等高线图了）：

contours = plt.contour(X, Y, Z, 3, colors='black')
plt.clabel(contours, inline=True, fontsize=8)
plt.imshow(Z, extent=[0, 5, 0, 5], origin='lower', cmap='RdGy', alpha=0.5)
plt.colorbar()

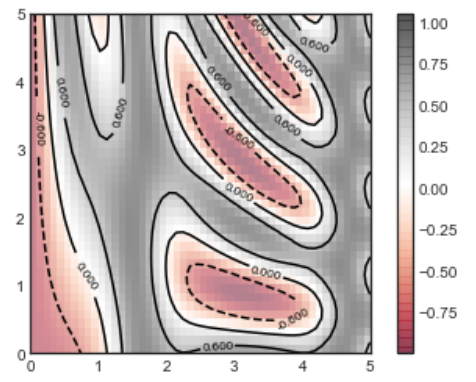
将 plt.contour() , plt.contourf() 以及 plt.imshow() 相结合，可以在三维图像可视化方面创造无限的可能！欲知更多，请看第 12 节使用 Matplotlib 绘制三维图像。