NumPy.random

numpy.random模块对Python内置的random进行了补充， 增加了一些用于高效生成多种概率分布的样本值的函数

  1. In [26]: samples = np.random.normal(size=(4,4))
  3. In [27]: samples
  4. Out[27]:
  5. array([[ 0.80595138,  0.94523723,  0.55290059, -0.49084826],
  6.        [ 2.76919288,  0.16045781, -1.34777518, -1.10624054],
  7.        [ 1.79839502, -1.05902345,  0.52886312,  0.08208192],
  8.        [-0.36451857, -0.27472158, -0.28468561,  0.88335674]])

可以用NumPy的 np.random.seed 更改随机数生成种子

  1. In [28]: np.random.seed(1234)

numpy.random的数据生成函数使用了全局的随机种子。 要避免全局状态， 你可以使用 numpy.random.RandomState ， 创建一个与其它隔离的随机数生成器

  1. In [29]: rng = np.random.RandomState(1234)
  3. In [30]: rng.randn(10)
  4. Out[30]:
  5. array([ 0.47143516, -1.19097569,  1.43270697, -0.3126519 , -0.72058873,
  6.         0.88716294,  0.85958841, -0.6365235 ,  0.01569637, -2.24268495])

numpy.random常用的函数
image.png
image.png

示例：随机漫步

下面是一个通过内置的random模块以纯Python的方式实现1000步的随机漫步

  1. In [31]: import random
  3. In [32]: position = 0
  5. In [33]: walk = [position]
  7. In [34]: steps = 1000
  9. In [35]: for i in range(steps):
  10.     ...:     step = 1 if random.randint(0, 1) else -1
  11.     ...:     position += step
  12.     ...:     walk.append(position)
  13.     ...:
  15. In [36]: import matplotlib.pyplot as plt
  17. In [37]: plt.plot(walk[:100])
  18. Out[37]: [<matplotlib.lines.Line2D at 0x27ba2734b48>]

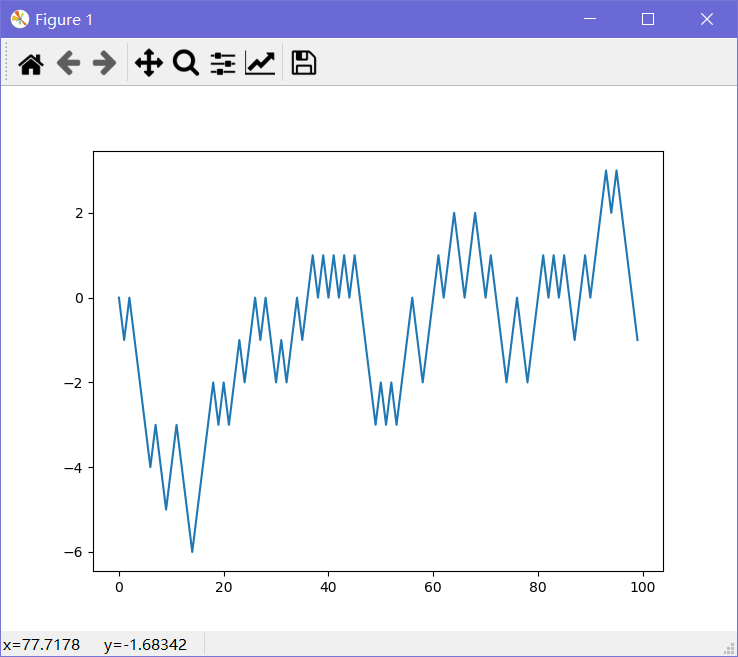
image.png
不难看出， 这其实就是随机漫步中各步的累计和 。用np.random模块一次性随机产生1000个“掷硬币”结果（即两个数中任选一个），将其分别设置为1或-1，然后计算累计和

  1. In [38]: nsteps = 1000
  3. In [39]: draws = np.random.randint(0, 2, size=nsteps)
  5. In [40]: steps = np.where(draws > 0, 1, -1)
  7. In [41]: walk = steps.cumsum()
  9. In [42]: walk.min()
  10. Out[42]: -9
  12. In [43]: walk.max()
  13. Out[43]: 60

现在来看一个复杂点的统计任务——首次穿越时间，即随机漫步过程中第一次到达某个特定值的时间。假设我想要知道本次随机漫步需要多久才能距离初始0点至少10步远（任一方向均可）。 np.abs(walk)>=10 可以得到一个布尔型数组，它表示的是距离是否达到或超过10，而我们想要知道的是第一个10或-10的索引。可以用argmax来解决这个问题，它返回的是该布尔型数组第一个最大值的索引（True就是最大值）

  1. In [44]: (np.abs(walk) >= 10).argmax()
  2. Out[44]: 297

注意，这里使用argmax并不是很高效，因为它无论如何都会对数组进行完全扫描。在本例中，只要发现了一个True，那我们就知道它是个最大值了

一次模拟多个随机漫步

如果你希望模拟多个随机漫步过程（比如5000个），只需对上面的代码做一点点修改即可生成所有的随机漫步过程。只要给numpy.random的函数传入一个二元元组就可以产生一个二维数组，然后我们就可以一次性计算5000个随机漫步过程（一行一个）的累计和了

  1. In [46]: nwalks = 5000
  3. In [47]: nsteps = 1000
  5. In [48]: draws = np.random.randint(0, 2, size=(nwalks, nsteps))
  7. In [49]: steps = np.where(draws > 0, 1, -1)
  9. In [50]: walks = steps.cumsum(1)
  11. In [51]: walks
  12. Out[51]:
  13. array([[  1,   2,   3, ...,  46,  47,  46],
  14.        [  1,   0,   1, ...,  40,  41,  42],
  15.        [  1,   2,   3, ..., -26, -27, -28],
  16.        ...,
  17.        [  1,   0,   1, ...,  64,  65,  66],
  18.        [  1,   2,   1, ...,   2,   1,   0],
  19.        [ -1,  -2,  -3, ...,  32,  33,  34]], dtype=int32)

计算所有随机漫步过程的最大值和最小值

  1. In [52]: walks.min()
  2. Out[52]: -128
  4. In [53]: walks.max()
  5. Out[53]: 122

得到这些数据之后，我们来计算30或-30的最小穿越时间。这里稍微复杂些，因为不是5000个过程都到达了30。 我们可以用any方法来对此进行检查：

  1. In [54]: hits30 = (np.abs(walks) >= 30).any(1)
  3. In [55]: hits30
  4. Out[55]: array([ True,  True,  True, ...,  True, False,  True])
  6. In [56]: hits30.sum() # Number that
  7. Out[56]: 3368

然后我们利用这个布尔型数组选出那些穿越了30（绝对值）的随机漫步（行），并调用argmax在轴1上获取穿越时间

  1. In [57]: crossing_times = (np.abs(walks[hits30]) >= 30).argmax(1)
  3. In [58]: crossing_times
  4. Out[58]: array([133, 395, 343, ..., 409, 297, 747], dtype=int64)