对角阵

image.png

  1. 提取矩阵的对角线元素

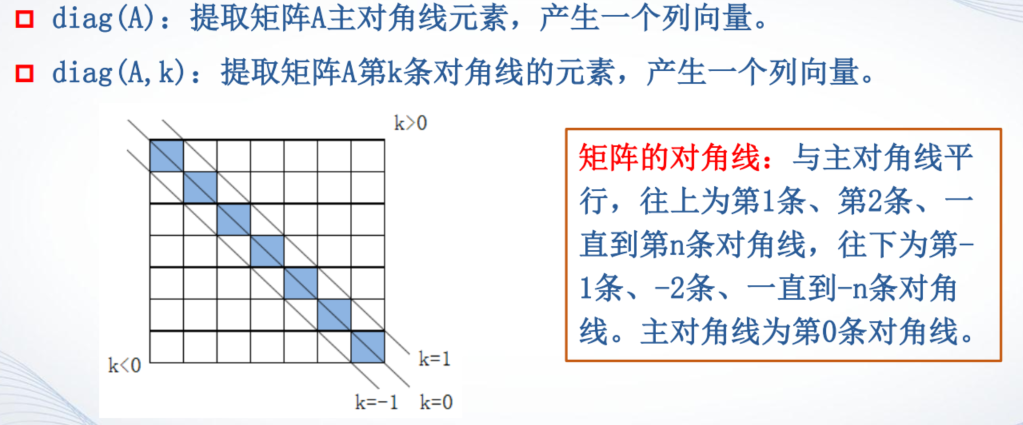
image.png

  1. 构造对角阵

image.png
先建立【MATLAB矩阵】矩阵变换 - 图4矩阵A，然后将A的第一行矩阵乘以1，第二行乘以2，…，第五行乘以5
image.png

  1. >> A = [7,0,1,0,5; 3,5,7,4,1; 4,0,3,0,2; 1,1,9,2,3; 1,8,5,2,9]
  2. A =
  3.        7              0              1              0              5       
  4.        3              5              7              4              1       
  5.        4              0              3              0              2       
  6.        1              1              9              2              3       
  7.        1              8              5              2              9       
  8. >> D = diag(1:5);
  9. >> D * A
  10. ans =
  11.        7              0              1              0              5       
  12.        6             10             14              8              2       
  13.       12              0              9              0              6       
  14.        4              4             36              8             12       
  15.        5             40             25             10             45

image.png

  1. >> D = diag(1:5);
  2. >> D * A
  3. ans =
  4.        7              0              3              0             25       
  5.        3             10             21             16              5       
  6.        4              0              9              0             10       
  7.        1              2             27              8             15       
  8.        1             16             15              8             45

对角阵

  1. 上三角阵

image.png

  1. >> triu(ones(4), -1)
  2. ans =
  3.        1              1              1              1       
  4.        1              1              1              1       
  5.        0              1              1              1       
  6.        0              0              1              1
  1. 下三角阵

image.png

矩阵的转置

image.png

  1. >> A = [1,3; 3+4i, 1-2i]
  2. A =
  3.        1        +    0i             3        +    0i      
  4.        3        +    4i             1        -    2i      
  5. >> A.'
  6. ans =
  7.        1        +    0i             3        +    4i      
  8.        3        +    0i             1        -    2i      
  9. >> A'
  10. ans =
  11.        1        +    0i             3        -    4i      
  12.        3        +    0i             1        +    2i

矩阵的旋转

image.png

  1. >> A = [1,3,2; -3,2,1; 4,1,2]
  2. A =
  3.        1              3              2       
  4.       -3              2              1       
  5.        4              1              2       
  6. >> rot90(A)
  7. ans =
  8.        2              1              2       
  9.        3              2              1       
  10.        1             -3              4 
  11. >> rot90(A, 2)
  12. ans =
  13.        2              1              4       
  14.        1              2             -3       
  15.        2              3              1

矩阵的翻转

image.png
验证魔方阵的主对角线、副对角线元素之和相等

  1. >> A = magic(5);
  2. >> D1 = diag(A);
  3. >> sum(D1)
  4. ans =
  5.       65       
  6. >> B = flipud(A);
  7. >> D2 = diag(B);
  8. >> sum(D2)
  9. ans =
  10.       65

矩阵的求逆

image.png
image.png

  1. >> A = [1,2,3; 1,4,9; 1,8,27]
  2. A =
  3.        1              2              3       
  4.        1              4              9       
  5.        1              8             27       
  6. >> b = [5;-2;6]
  7. b =
  8.        5       
  9.       -2       
  10.        6       
  11. >> x = inv(A) * b
  12. x =
  13.       23       
  14.      -29/2     
  15.       11/3     
  16. >> x = A\b
  17. x =
  18.       23       
  19.      -29/2     
  20.       11/3