对于任意的科学观测，准确的度量误差甚至比准确的度量数据本身更加重要。
当然，搞事情之前还是需要四连：

%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')
import numpy as np

1 基本误差图

可以直接使用 plt.errorbar() 来绘制误差条：

x = np.linspace(0, 10, 50)
dy = 0.8
y = np.sin(x) + dy * np.random.rand(50)
plt.errorbar(x, y, yerr=dy, fmt='.k')

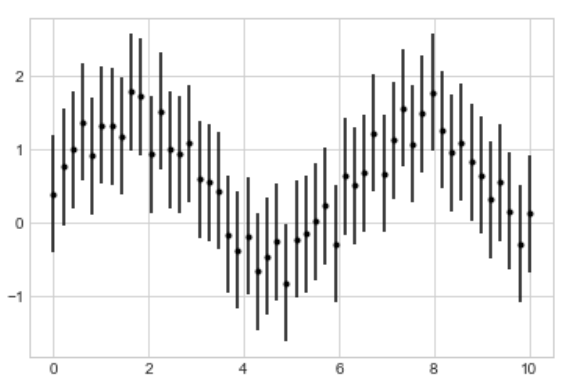
其中 fmt 参数跟前面讲的 plt.plot() 中控制曲线样式的语法是一样的； yerr 控制的是误差的绝对值，即图中每一条竖线代表的范围是 3 误差图 Errorbars - 图2 .

除了上面这些基本的功能外， plt.errorbar() 还有很多对输出图表进行微调的操作，比如让坐标点 (x, y) 更加突出，而竖线变得轻一点：

plt.errorbar(x, y, yerr=dy, fmt='o', color='black',
             ecolor='lightgray', elinewidth=3, capsize=0)

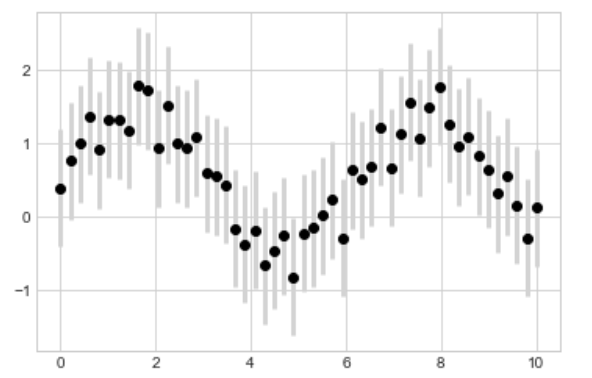
当然还有更多更多其他的选项，比如画出水平线上的误差 xerr 等其他变种。更多资讯好玩的用法详见 plt.errorbar() 的官网文档。

2 连续域上的误差

上一节中数据明显是离散的，但很多情况下我们还是会处理在连续域上的误差（虽然计算机只能处理离散的东西，但是我们将离散的数据变的足够多，不就“连续”了么）。虽然 Matplotlib 没有提供一个这样的函数，但是我们可以使用最原始的 plt.plot() + plt.fill_between() 来达到这样的效果。

接下来我们利用 Scikit-Learn API 中提供的高斯过程回归 ( Gaussian process regression ) 来做一个小例子。

from sklearn.gaussian_process import GaussianProcessRegressor
# Define the model and draw some data
model = lambda x: x * np.sin(x)
x_data = np.array([1, 3, 5, 6, 8])
y_data = model(x_data)
# Compute the Gaussian process fit
gp = GaussianProcessRegressor(random_state=100)
gp.fit(x_data[:, np.newaxis], y_data)
x_fit = np.linspace(0, 10, 1000)
y_fit, MSE = gp.predict(x_fit[:, np.newaxis], return_std=True)
dy_fit = 2 * np.sqrt(MSE) # 2*sigma ~ 95% confidence region

其中 x_fit , y_fit 以及 dy_fit 是我们用来拟合源数据的连续样本。如果我们使用上面的 plt.errorbar() 则只能画出来 1000 个点和 1000 个误差条。而在 plt.fill_between() 中我们使用较浅的颜色来标识连续变量的误差肯定效果更好：

plt.plot(x_data, y_data, 'or')
plt.plot(x_fit, y_fit, '-', color='gray')
plt.fill_between(x_fit, y_fit - dy_fit, y_fit + dy_fit, color='gray', alpha=0.2)
plt.xlim(0, 10)

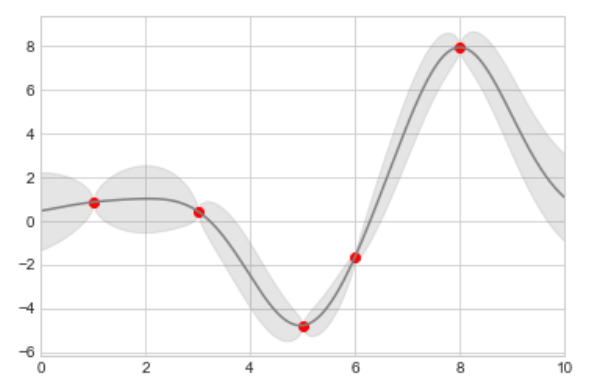
从上图中我们可以总结出高斯过程回归的误差特点：在靠近训练集数据点的地方误差收敛的很好，而在远离这些点的地方误差呈现发散的态势，一般情况下离得越远误差越大。

更多关于 plt.fill_between() 的选项，以及与它非常像的 plt.fill() 函数，可以查看官方文档！

最后，Matplotlib 确实在连续误差上没有太大建树，如果想整点高级玩意，请看使用 Seaborn 进行可视化章节！