特征值和特征向量的命令

image.png

  1. >> A = [1,1,0;1,0,5;1,10,2]
  2. A =
  3.      1     1     0
  4.      1     0     5
  5.      1    10     2
  6. >> [X,D] = eig(A)
  7. X =
  8.     0.0722    0.9751    0.0886
  9.     0.5234   -0.0750   -0.6356
  10.     0.8490   -0.2089    0.7669
  11. D =
  12.     8.2493         0         0
  13.          0    0.9231         0
  14.          0         0   -6.1723

验证特征向量和特征值的定义

  1. >> A * X(:, 1)
  2. ans =
  3.     0.5956
  4.     4.3174
  5.     7.0040
  6. >> D(1) * X(:,1)
  7. ans =
  8.     0.5956
  9.     4.3174
  10.     7.0040

【例题】
image.png

  1. >>R = [-1,2,0;2,-4,1;1,1,-6]
  3. R =
  4.     -1     2     0
  5.      2    -4     1
  6.      1     1    -6
  7. >> S = [1,2;2,3]
  8. S =
  9.      1     2
  10.      2     3
  11. >> A = [R, zeros(3,2); zeros(2,3), S];
  12. >> [X1,D1] = eig(R)
  14. X1 =
  15.     0.8553    0.4517    0.1899
  16.     0.4703   -0.8395   -0.5111
  17.     0.2173   -0.3021    0.8383
  18. D1 =
  19.     0.0996         0         0
  20.          0   -4.7165         0
  21.          0         0   -6.3832
  22. >> [X2,D2] = eig(S);
  23. >> [X3,D3] = eig(A);
  24. >> X2
  25. X2 =
  26.    -0.8507    0.5257
  27.     0.5257    0.8507
  28. >> D2
  29. D2 =
  30.    -0.2361         0
  31.          0    4.2361
  32. >> X3
  33. X3 =
  34.     0.8553    0.4517    0.1899         0         0
  35.     0.4703   -0.8395   -0.5111         0         0
  36.     0.2173   -0.3021    0.8383         0         0
  37.          0         0         0   -0.8507   -0.5257
  38.          0         0         0    0.5257   -0.8507
  39. >> D3
  40. D3 =
  41.     0.0996         0         0         0         0
  42.          0   -4.7165         0         0         0
  43.          0         0   -6.3832         0         0
  44.          0         0         0   -0.2361         0
  45.          0         0         0         0    4.2361

特征值的几何意义

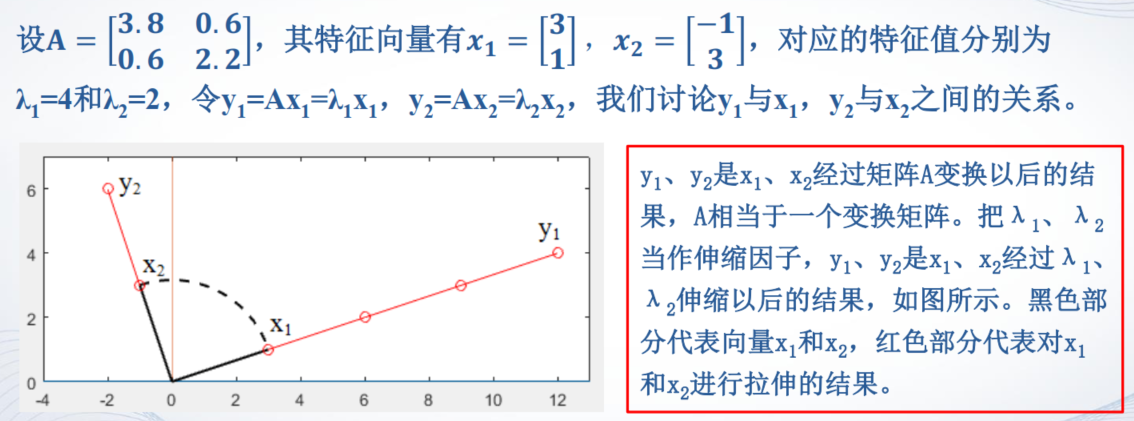
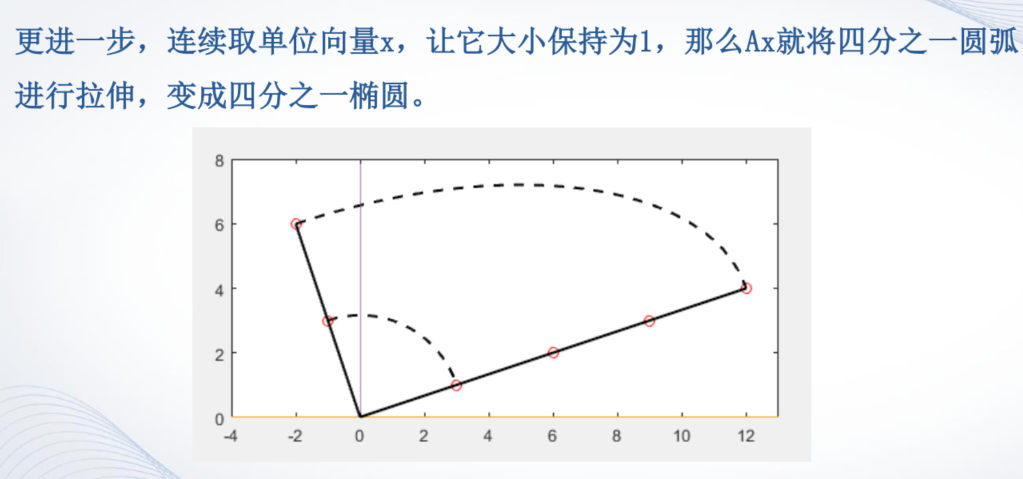
image.png
image.png
image.png
【例题2】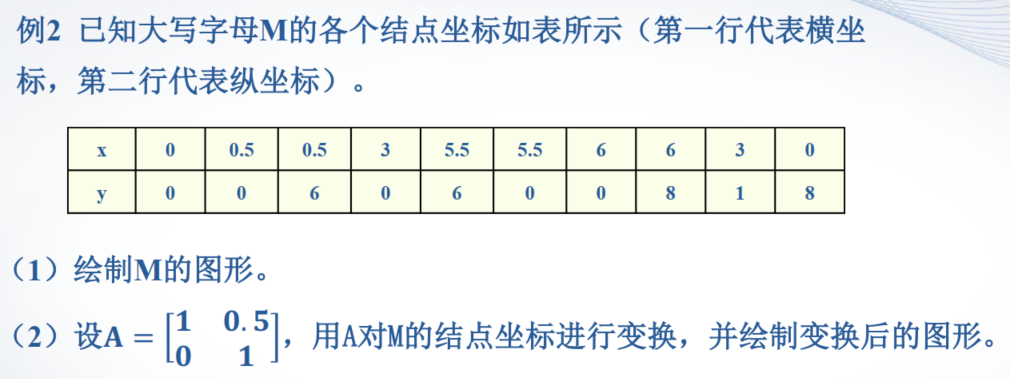
image.png

  1.     >> x = [0,0.5,0.5,3,5.5,5.5,6,6,3,0;0,0,6,0,6,0,0,8,1,8];
  2. >> A = [1,0.5;0,1]
  3. >> y = A*x;
  4. >> subplot(2, 2, 1);
  5. >> fill(x(1,:), x(2:), 'r');
  6. >> fill(x(1,:), x(2,:), 'r');
  7. >> subplot(2, 2, 2);
  8. >> fill(y(1,:), y(2,:), 'r');

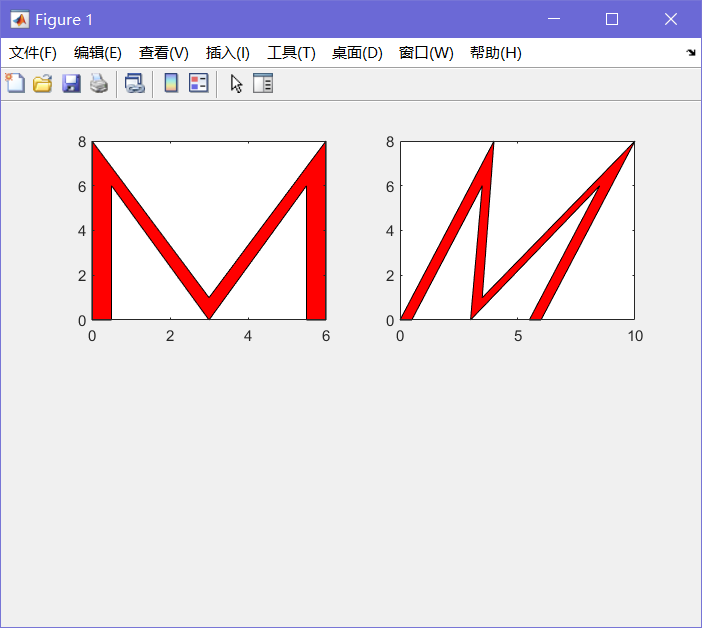
image.png
所以斜体字体可以由普通的字体通过线性变换生成，这样可以减少存储空间