方阵的行列式

>> format rat
>> A = [1,3,2; -3,2,1; 4,1,2]
A =
       1              3              2       
      -3              2              1       
       4              1              2       
>> det(inv(A))
ans =
       1/11    
>> 1 / det(A)
ans =
       1/11

矩阵的秩

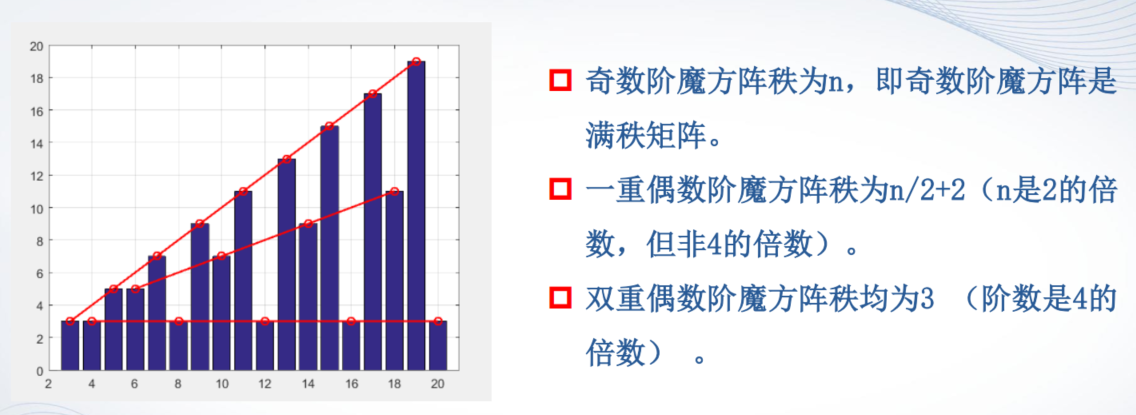
求3~20阶魔方阵的秩

>> for n = 3:20
      r(n) = rank(magic(n));
end
>> bar(r)

矩阵的迹

向量和矩阵的范数

1. 向量的三种常用范数

1. 矩阵的范数

>> x = [2 0 1; -1 1 0; -3 3 0]
x =
       2              0              1       
      -1              1              0       
      -3              3              0       
>> n = norm(x)
n =
    4.7234
>> n = norm(x, 1)
n =
     6

矩阵的条件数

求2~10阶希尔伯特矩阵的条件数

>> for n = 2:10
c(n) = cond(hilb(n));
end
>> format long
>> c'
ans =
   1.0e+13 *
                   0
   0.000000000001928
   0.000000000052406
   0.000000001551374
   0.000000047660725
   0.000001495105864
   0.000047536735691
   0.001525757556663
   0.049315340455101
   1.602502816811318