直方图是我们常常可以作为我们理解数据集的第一步，也是重要一步。

一维直方图绘制

首先还是基操：

%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('seaborn-white')
import numpy as np
data = np.random.randn(1000)

plt.hist(data)

当然 plt.hist() 函数还有很多可选参数：

plt.hist(data, bins=30, density=True, alpha=0.5, 
         histtype='stepfilled', color='steelblue',
         edgecolor='none')

• bins —- 直方图中箱子 ( bins ) 的数量
• density —- 如果该参数为 True ，则将直方图正则化，也即直方图下方的面积和为 1.

直接查看 plt.hist() 的官方文档还是更靠谱的，每个参数都解释的很明白。
histtype='stepfilled'** 与透明度 alpha 一起使用以在直方图中对比不同数据的分布效果更佳呦！**

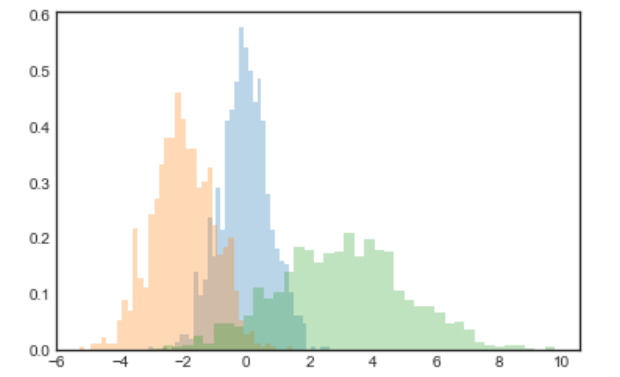
x1 = np.random.normal(0, 0.8, 1000)
x2 = np.random.normal(-2, 1, 1000)
x3 = np.random.normal(3, 2, 1000)
kwargs = dict(histtype='stepfilled', alpha=0.3, density=True, bins=40)
plt.hist(x1, **kwargs)
plt.hist(x2, **kwargs)
plt.hist(x3, **kwargs)

需要说明的是， plt.hist() 是有返回值的。如果我们只想计算直方图参数（计算每一个 bins 中点的数量）而不把直方图画出来，那么可以使用 np.histogram() ：

>>> counts, bin_edges = np.histogram(data, bins=5)
>>> print(counts, bin_edges)
[ 18 200 432 302  48] [-3.35181513 -2.10033581 -0.84885649  0.40262284  1.65410216  2.90558149]

二维直方图绘制

上面我们在绘制一维直方图的时候，通过将一条数轴（x 轴）划分成多个 bins 的方法画出了直方图。那么二维直方图同理，要将一个个二维点分入不同的 bins 里面。比如下面我们定义了一些服从多变量高斯分布的数据点：

mean = [0, 0]
cov = [[1, 1], [1, 2]]
x, y = np.random.multivariate_normal(mean, cov, 10000).T

plt.hist2d() : 二维直方图

plt.hist2d(x, y, bins=30, cmap='Blues')
cb = plt.colorbar()
cb.set_label('counts in bins')

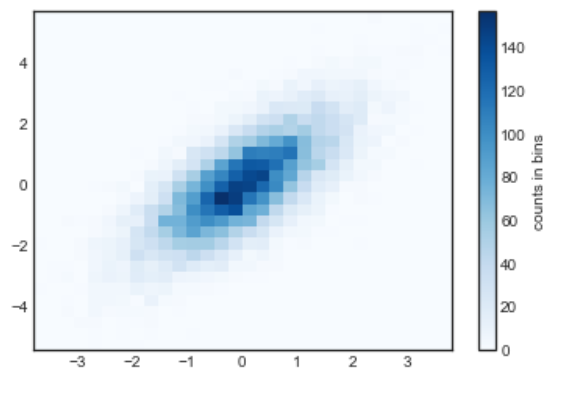
与 plt.hist() 一样， plt.hist2d() 也有在 Numpy 中对应的函数 np.histogram2d() :

counts, xedges, yedges = np.histogram2d(x, y, bins=30)

如果想得到高于二维的直方图参数，可以使用 np.histogramdd() 函数

plt.hexbin() : 六边形 bins

上面画出来的直方图使用正方形进行密铺，另外一种常用的密铺形状是正六边形。Matplotlib 也提供了相应的接口：

plt.hexbin(x, y, gridsize=30, cmap='Blues')
cb = plt.colorbar(label='count in bin')

plt.hexbin() 提供了一堆有意思的可选参数，比如可以指明每一个点的权重，改变返回值的形式等，详见该函数的 docstring.

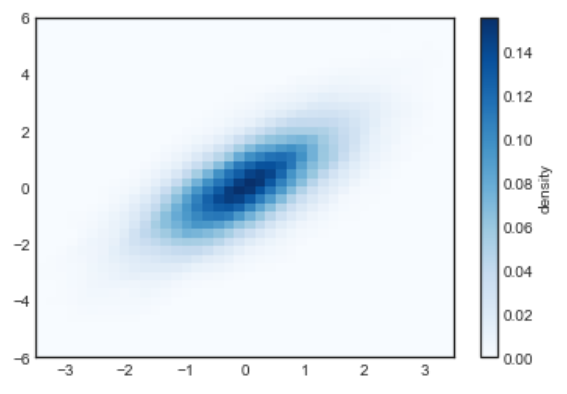
核密度估计 Kernel density estimation

另外一个估计高维数据的密度的方法是核密度估计 (KDE, Kernel Density Estimation). 可以使用 scipy.stats 包直接整！

from scipy.stats import gaussian_kde
# fit an array of size [Ndim, Nsamplpes]
data = np.vstack([x, y])
kde = gaussian_kde(data)
# evaluate on a regular grid
xgrid = np.linspace(-3.5, 3.5, 40)
ygrid = np.linspace(-6, 6, 40)
Xgrid, Ygrid = np.meshgrid(xgrid, ygrid)
Z = kde.evaluate(np.vstack([Xgrid.ravel(), Ygrid.ravel()]))
# Plot the result as an image
plt.imshow(Z.reshape(Xgrid.shape),
           origin='lower', aspect='auto',
           extent=[-3.5, 3.5, -6, 6],
           cmap='Blues')
cb = plt.colorbar()
cb.set_label('density')