通用的特殊矩阵

image.png
image.png

  1. >> A = zeros(2, 3)
  2. A =
  3.      0     0     0
  4.      0     0     0
  5. >> zeros(size(reshape(A, 3, 2)))
  6. ans =
  7.      0     0
  8.      0     0
  9.      0     0

image.png

  1. >> A = fix(10 + (99-10+1) * rand(5));
  2. >> B = 0.6 + sqrt(0.1) * randn(5);
  3. >> C = eye(5);
  4. >> (A+B)*C == A*C + B*C
  5. ans =
  6.   5×5 logical 数组
  7.    1   1   1   1   1
  8.    1   1   1   1   1
  9.    1   1   1   1   1
  10.    1   1   1   1   1
  11.    1   1   1   1   1

用于专门学科的特殊矩阵

  1. Magic Square 魔方矩阵

    1. >> M = magic(3)
    2. M =
    3.   8     1     6
    4.   3     5     7
    5.   4     9     2

    image.png

  2. 范德蒙矩阵

image.png

  1. >> vander(1:5)
  2. ans =
  3.      1     1     1     1     1
  4.     16     8     4     2     1
  5.     81    27     9     3     1
  6.    256    64    16     4     1
  7.    625   125    25     5     1
  1. 希尔伯特矩阵

image.png

  1. >> format rat % 使用有理数输出
  2. >> H = hilb(4)
  3. H =
  4.        1              1/2            1/3            1/4     
  5.        1/2            1/3            1/4            1/5     
  6.        1/3            1/4            1/5            1/6     
  7.        1/4            1/5            1/6            1/7

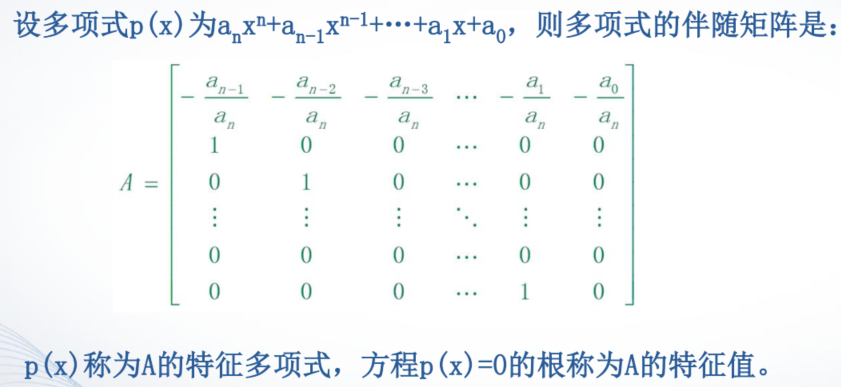
image.png

  1. 伴随矩阵

image.png
image.png

  1. 帕斯卡矩阵

image.png
image.png
生成5阶帕斯卡矩阵，验证它的逆矩阵的所有元素也为整数

  1. >> format rat
  2. >> P = pascal(5)
  3. P =
  4.        1              1              1              1              1       
  5.        1              2              3              4              5       
  6.        1              3              6             10             15       
  7.        1              4             10             20             35       
  8.        1              5             15             35             70       
  9. >> inv(P)
  10. ans =
  11.        5            -10             10             -5              1       
  12.      -10             30            -35             19             -4       
  13.       10            -35             46            -27              6       
  14.       -5             19            -27             17             -4       
  15.        1             -4              6             -4              1