NeRF 神经辐射场

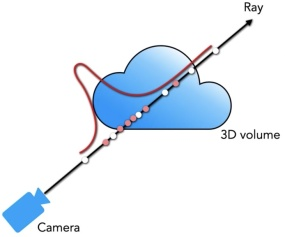
基于标准的神经辐射场场景表示(Neural Radiance Field scene representation)[30]，并受Gafni等人[16]介绍的面部动画动态神经辐射场的启发，我们提出了一个条件辐射场的说话头部使用条件隐式函数和一个额外的音频代码作为输入。

Neural Radiance Field(NeRF)

Mildenhall B, Srinivasan P P, Tancik M, et al. Nerf: Representing scenes as neural radiance fields for view synthesis[C]//European Conference on Computer Vision. Springer, Cham, 2020: 405-421.

本文的贡献如下：

• 包含复杂几何和材质的连续场景的表示方法：使用参数化为 MLP 的 5D 神经辐射场；
• 基于立体渲染技术的可导的渲染流程，用于网络的优化。其中还包括层次化的采样策略，专注于可见的场景内容（visible scene content），充分利用了 MLP 的容量。
• 使用位置编码，将输入 5D 坐标映射到更高维的空间，让 NeRF 可以学习表示高频的场景内容。

NeRF可以简要概括为用一个MLP神经网络从2D图片中隐式地学习静态3D场景。通过沿着相机光线（camera rays）获取 5D 坐标，使用经典的立体渲染（volume rendering）技术，我们将输出的颜色和密度投影到图像上，从而实现视图合成。

3 神经辐射场的场景表示

流程图：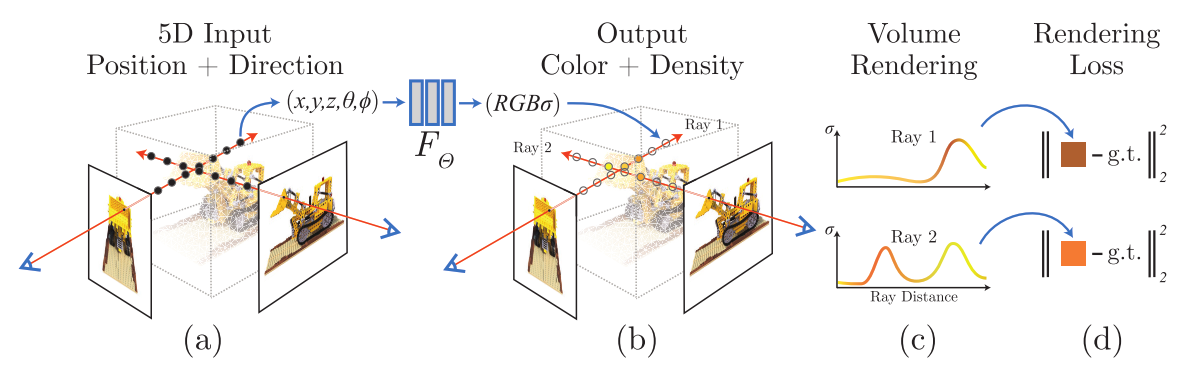

Fig. 2: 神经辐射场场景表示和可导的渲染流程概述。我们的图像合成，通过（图 a）沿着相机光线采样出 5D 坐标（位置和视角方向）；（图 b）把位置喂给 MLP，生成颜色和体积密度；（图 c）使用立体渲染技术，利用这些值得到一张图像。由于这个渲染函数是可导的，因此我们可以最小化合成图像和真实观察图像的残差，进行场景表示的优化。

为了根据某一视角（viewpoint），渲染出这个神经辐射场（Neural Radiance Field, NeRF），我们：

1. 使相机光线穿过场景，生成一组 3D 采样点；
2. 让这些 3D 点和对应的视角方向作为神经网络的输入，生成一组颜色和密度；
3. 使用经典的立体渲染技术，累加这些颜色和密度，得到 2D 图像。

NeRF函数是将一个连续的场景表示为一个输入为5D向量的函数，包括一个空间点的3D坐标位置 x=(x,y,z) ，以及视角方向 d=(θ,ϕ) 。这个神经网络可以写作：FΘ:(x,d)→(c,σ)。其中， σ是对应3D位置（或者说是体素）的密度，而 c=(r,g,b) 是视角相关的该3D点颜色。
我们约束了预测体积密度 σ 的网络的输入仅仅是位置 X，而预测 RGB 颜色 C 的网络的输入是位置和视角方向，通过这种方式可以鼓励网络学习到多视角连续的表示。

• 在具体实现上，MLP FΘ 首先用 8 层的全连接层（使用 ReLU 激活函数，每层有 256 个通道），处理 3D 坐标 x，得到 σ 和一个 256 维的特征向量。
• 这个 256 维的特征向量，与视角方向一起拼接起来，喂给另一个全连接层（使用 ReLU 激活函数，每层有 128 个通道），输出方向相关的 RGB 颜色。

简单来说就是，坐标 x 输入到MLP网络中，并输出 σ 和中间特征，中间特征和视角方向 d 再输入到额外的全连接层中并预测颜色。因此，体素密度只和空间位置有关，而颜色则与空间位置以及观察的视角都有关系。

4 辐射场的立体渲染

体积密度 σ(x) 可以解释为：光线停留在位置 X 处的无穷小粒子的可导概率。
在最近和最远边界为 tn 和 tf 的条件下，相机光线 r(t)=o+td 的颜色 C(r) 为：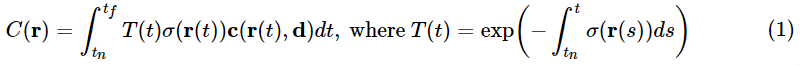

函数 T(t) 表示沿着光线从 tn 到 t 所累积的透明度（accumulated transmittance），即光线从 tn 出发到 t，穿过该路径的概率。视图的渲染需要求这个积分 C(r)，它是就是虚拟相机穿过每个像素的相机光线，所得到的颜色。
我们使用求积法（quadrature）进行积分的数值求解。确定性的求积分不太适合 MLP，我们采用的是分层抽样（stratified sampling）的方法。我们把 [tn,tf] 分成均匀分布的小区段，接着对每个小区段进行均匀采样：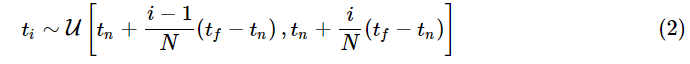

5 神经辐射场的优化

前面所述的核心算法，还不够实现最先进的效果。因此我们还引入了两项优化措施，帮助模型能够表征高分辨率的复杂场景：

1. 输入坐标的位置编码（positional encoding）：帮助 MLP 能够表示高频函数；

NeRF函数的输入为位置和角度信息，作者发现直接将位置和角度作为网络的输入得到的结果是相对模糊的（见实验部分）。而用positon encoding 的方式将位置信息映射到高频则能有效提升清晰度效果。具体而言，这里采用的是与Transformer 中类似的正余弦周期函数的形式。
与 Transformer 架构中使用的位置编码不同，我们这里的编码函数，是为了把连续的输入坐标映射到更高维的空间，好让 MLP 能够更好地近似高频的函数。

1. 层次化的采样方案（hierarchical sampling procedure），可以有效地采样模型的高频表示。

NeRF的渲染过程计算量很大，每条射线都要采样很多点。但实际上，一条射线上的大部分区域都是空区域，或者是被遮挡的区域，对最终的颜色没有啥贡献。因此，作者采用了一种“coarse to fine” 的形式，同时优化coarse 网络和 fine 网络。
首先对于coarse 网络，我们可以采样较为稀疏的 Nc 个点，并将前述的离散求和函数重新表示，计算沿着射线的概率密度函数（PDF），如下图所示。通过这个概率密度函数，我们可以粗略地得到射线上物体的分布情况。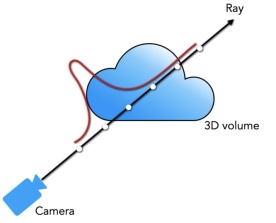

接下来，基于得到的概率密度函数来采样 Nf 个点，并用这 Nf 个点和前面的 Nc 个点一同计算fine 网络的渲染结果。虽然coarse to fine 是计算机视觉领域中常见的一个思路，但这篇方法中用coarse 网络来生成概率密度函数，再基于概率密度函数采样更精细的点算的上是很有趣新颖的做法了。二阶段的采样示意图如下所示：

参考