01. 数据结构与算法基本概念

01. 数据结构与算法的重要性

• Pascal语言之父Nicklaus Wirth（尼古拉斯·沃斯）凭借着“程序=数据结构+算法”这个公式获得了图灵奖。
• 尼古拉斯·沃斯提出的这个公式对计算机科学的影响程度足以类似于物理学中爱因斯坦的（质能方程）。

• “程序=数据结构+算法”这个公式展示了程序的本质，即想要编写出一个好的程序，就必须要懂得数据结构与算法。

  02. 数据结构的基本认识

  2.1 数据结构的研究内容举例

  2.1.1 数学模型

• 通常，用计算机解决一个问题的步骤为：将具体的问题抽象为数学模型；设计算法；编程、调试、运行。

• 其中，将具体问题转换为数学模型的实质是：
  • 分析具体问题，从问题中提取出计算机程序可操作的对象。
  • 接着，分析这个问题中不同操作对象之间的关系。
  • 然后将操作对象以及对象之间的关系用数学语言描述出来，这里所谓的操作对象以及对象之间的关系指的就是数据结构。
  • 最后，让计算机帮助求解描述出来的数学语言。
• 几个例子：
  • 例题1：求解梁架结构中的应力。

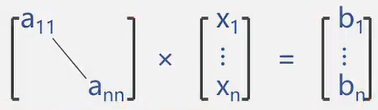
• 例题2：预报人口增长情况。

数学模型（微分方程）：

• 上述两个问题的结果步骤都是：
  • 首先分析问题、提取操作对象。
  • 然后找出操作对象执行的关系，用数学语言加以描述，建立数学方程。
  • 最后，让计算机帮助求解数学方程，如高斯消元法、有限元法、差分法……。
    • 寻找数据元素之间的关系是比较简单的，但是计算会比较复杂，但是计算机的优势就是计算。

      2.1.2 非数值计算

• 随着计算机应用领域的扩展，计算机被越来越多的用于非数值计算。
• 如计算机学院学生学籍管理系统中有如下的一张表。这时候从其他学院转来一位同学，那么就要将这位同学的学籍数据添加到表中；一位同学退学了，就需要将这位同学的学籍数据从表中移除；一位同学从计科专业转到了大数据专业，那么就需要更改表中这位同学对应的数据；老师需要知道某位同学籍贯，就需要到这张表中查询这位同学的数据。

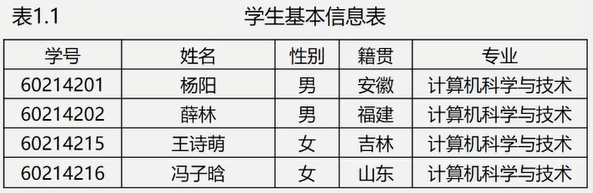
• 在上述四个例子中：

  • 操作对象：每位学生的信息（学号、姓名、性别、籍贯、专业、……），不再是简单的数值数据了。
  • 操作算法：查询、插入、修改、删除等。
  • 操作对象之间的关系：线性关系（一对一的关系）。
  • 数据结构：线性数据结构（线性表）。

    2.1.3 决策问题

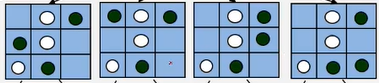
• 现有一个井字棋游戏的布局如下：

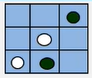
• 这种情况下白子的派生格局有：（2,1）、（1,1）、（1,2）、（2,3）、（3,3）五种。（派生格局指当前情况可能出现的下一种情况的集合）

• 假如白子落在了（1,2）位置上，那么此时黑子的派生格局为：（2,1）、（1,1）、（2,3）、（3,3）四种。

• 由此一般般形成的数据结构就是树结构：

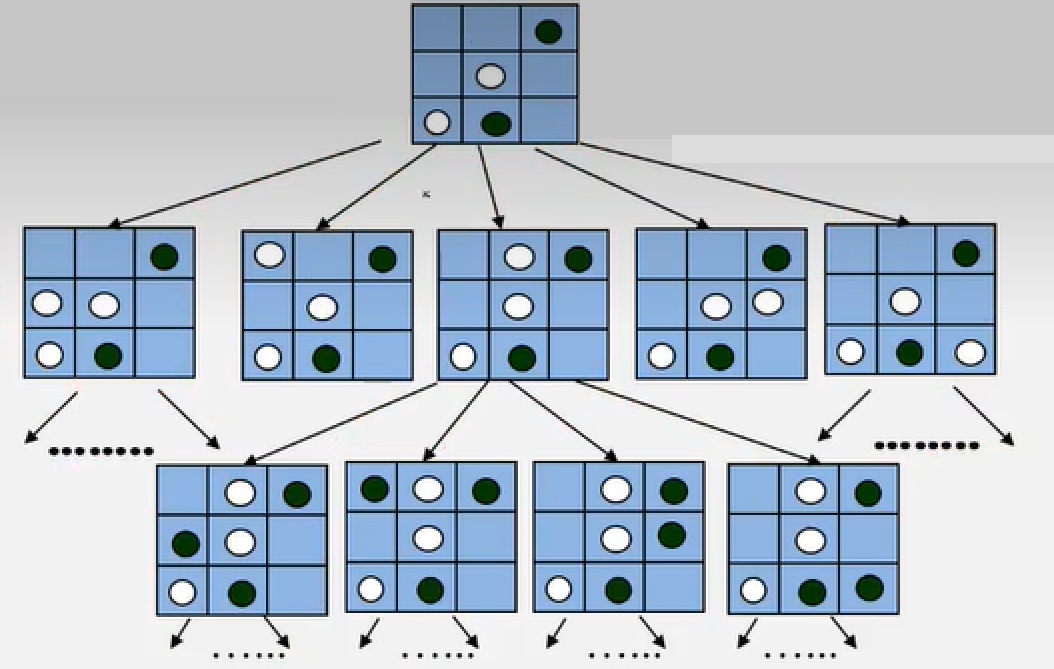
• 这种游戏计算机判断输赢的策略为：每一步的派生格局都已经输入计算机，因此可以根据当前棋盘的格局来预测棋局发展的趋势，甚至最后的结局。

  • 计算机的操作对象为：各种棋局状态，即描述棋盘的格局信息。
  • 操作对象之间的关系：非线性关系（一对多的关系）。
  • 数据结构：非线性结构（树，一个父节点可以有多个子节点，一个子节点只能属于一个父节点）。
  • 计算机的算法：走棋，即选择一种策略使棋局状态发生变化。（由一个格局派生出另一个格局）

    2.1.4 地理信息处理

• 百度地图、高德地图这些软件的导航（即寻求最短路径，或最快路径）功能是使用图数据结构来完成的。

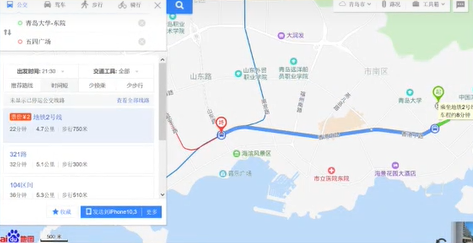
• 计算机处理的方式：
  • 将真实地图上的地点抽象成一个个的节点，将真实地图上的道路抽象成点与点之间的连线。
  • 由此就可以抽象出一个由点和边构成的网状结构，这个网状结构结构称之为图结构。
  • 接着，让计算机分析出点到点之间的最短路径即可。

2.1.5 总结

• 计算机可以解决数学问题（最简单的，直接套公式算出来的问题）。
• 计算机也可以解决无法用数学的公式或方程描述出来的“非数值计算”的程序设计问题。
• 非数值计算问题的数学模型不再是数学方程了，而是诸如表、树和图之类的具有逻辑关系的数据结构。

• 由此可以得出，数据结构是一门研究非数值计算的程序设计中计算机的操作对象以及它们之间的关系和操作的学科。

  2.2 数据结构中的一些基本概念

  2.2.1 数据、数据元素、数据项、数据对象

• 数据（Data）：

  • 想要计算机帮助我们处理问题，就需要把现实世界中的信息抽象到计算机中。
  • 能够输入计算机且能够被计算机处理的各种符号的集合就被称为数据。
  • 数据是信息的载体，是对客观事物符号化的表示，能够被计算机识别、存储和加工。
  • 数据包括数值型数据（整数、实数等），这类数据通常表示可以进行加、减、乘、除、平方、开方等算术运算的数据；以及非数值型数据（文字、图像、图形、声音等），即无法进行算术运算的其他数据。
• 数据元素（Data Element）：
  • 有些数据之间关系比较紧密，在操作时需要作为一个整体进行操作。
  • 如下表中的每一条数据中还有学号、姓名、性别、出生日期、政治面貌等数据。通常来说某一位的学号、姓名、性别、出生日期、政治面貌通常需要作为一个整体来操作，比如某位同学转学了，那么这位同学的学号、姓名、性别、……都要删除；或者是转入了一位新同学，那么这位同学的学号、姓名、性别、……都要输入。

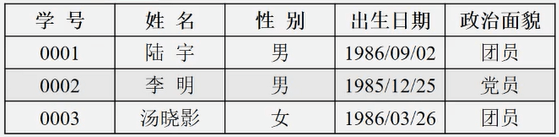
• 数据元素是数据的基本单位，像数据表中一条记录的这种在计算机程序中通常作为一个整体进行考虑和处理的数据基本单位称之为数据元素。
• 数据元素也可以简称为元素，或称之为记录（表格中常用）、结点（树结构中常用）或顶点（图结构中常用）。
  • 数据项（Data Item）：
• 数据项是构成数据元素的不可分割的最小单位。
• 如上表中的一条记录包含学号、姓名、性别、出生日期、政治面貌这五个数据项。
  • 数据、数据元素、数据项之间的关系：
• 数据是由数据元素组成的，数据元素是由数据项组成的。
• 如一张学生表（数据）中有多条学生的个人记录（数据元素），而一条个人记录由学号、姓名、性别、出生日期、政治面貌这五个数据项组成。
  • 数据对象（Data Object）：
• 数据对象是数据中有相同性质的数据元素的集合，是数据的一个子集。
• 例如：整数数据对象是集合、大写字母数据对象是集合、……。
• 数据元素与数据对象的关系：
  • 数据元素是组成数据的基本单位，是数据这个集合中的个体。
  • 数据对象是性质相同的数据元素的集合，是数据这个集合的子集。

    2.2.2 数据结构

• 数据结构的基本概念：
  • 数据元素不是孤立存在的，它们之间存在着某种关系，数据元素之间的关系称为结构（Structure）。
  • 数据结构（Data Structure）是指相互之间存在一种或多种特定关系的数据元素集合，或者说数据结构是带结构的数据元素的集合。
• 数据结构包含逻辑结构、存储结构、运算和实现三部分内容：
  • 数据的运算和实现：即对数据元素可以施加的操作以及这些操作在相应的存储结构上的实现。
• 逻辑结构：
  • 逻辑结构用于描述数据元素之间的逻辑关系。
  • 逻辑结构是独立于计算机存在的，与数据的存储无关，是从具体问题中抽象出来的数学模型。
• 物理结构（存储结构）：
  • 数据元素及其关系在计算机的存储器（内存）中的表示称为数据的物理结构或者数据的存储结构。
  • 这种结构简单来说就是指数据在计算机中的存储方式，与逻辑结构不同，物理结构是依赖于计算机存在的。
• 逻辑结构与存储结构的关系：
  • 存储结构是逻辑关系的映像与元素本身的映像。
  • 逻辑结构是数据结构的抽象，存储结构是数据结构的实现。
  • 逻辑结构与存储结构综合起来建立了数据元素之间的结构关系。
• 逻辑结构的种类：
  • 逻辑结构可以分为线性结构和非线性结构。
  • 线性结构：
    • 有且仅有一个开始节点和一个终端节点，并且所有节点都最多只有一个直接前趋和一个直接后继。
    • 线性结构中的数据元素之间存在着一对一的线性关系。
    • 常见的线性结构有：线性表（数组、链表）、栈、队列、串。
  • 非线性结构：
    • 一个节点可能有多个直接前趋和多个直接后继。
    • 非线性结构中的数据元素之间存在着一对多或者是多对多的关系。
    • 常见的非线性结构有：树（一对多的层次关系）、图（多对多的任意关系）。
  • 有些分类中还会单独存在一类集合结构，所谓集合就是结构中的数据元素之间除了同属于一个集合的关系外，无任何其他关系。

• 存储结构的种类：
  • 存储结构可以分为顺序存储结构、链式存储结构、索引存储结构、散列存储结构四种。
• 
  
• 
  
• 
  
• 
  
• 
  

• 阿斯顿

  03. 算法和算法分析

• 阿斯顿8