01. 函数
1.1 函数的基本概念
- 函数用于描述量与量之间的关系，如：
描述的就是变量A与变量r之间的关系。 - 函数中存在着自变量与因变量，如：
中x是自变量，y是因变量。 - 随着自变量x的变化，因变量y也会发生变化，那么函数在
处取得的函数值即可描述为
。 上述函数
只是一种符号表示，当然也可以写成：
、
、
、……分段函数：
- 反函数：
显函数与隐函数：
奇偶性：
- 奇函数：
，如
；奇函数图像关于原点对称。
- 奇函数：
，如：
，如：
、
- 偶函数：
，如：
；偶函数图像关于y轴对称。
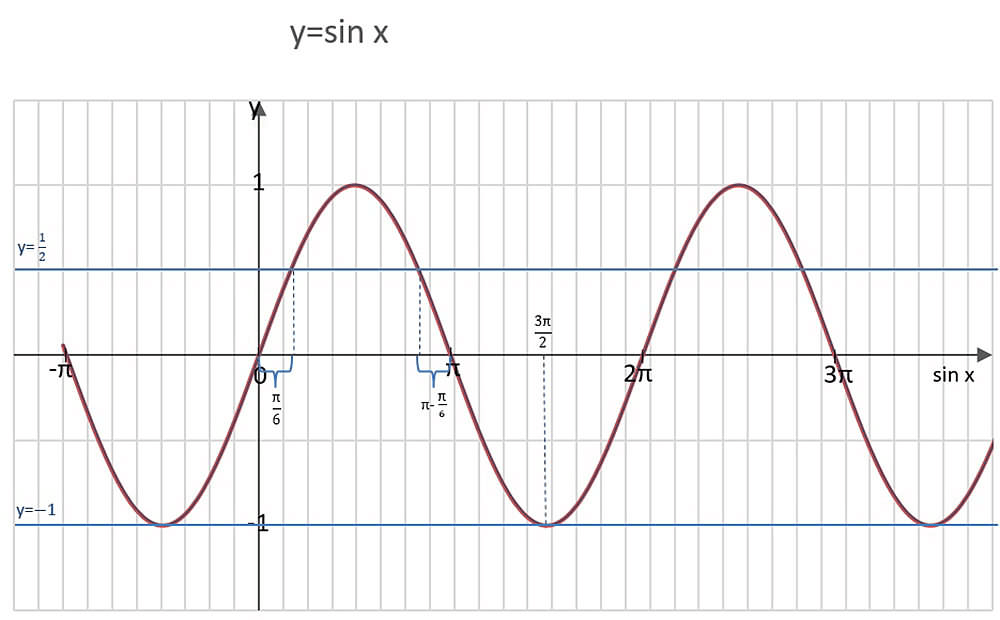
- 周期性：
，常见于
、
等三角函数中。
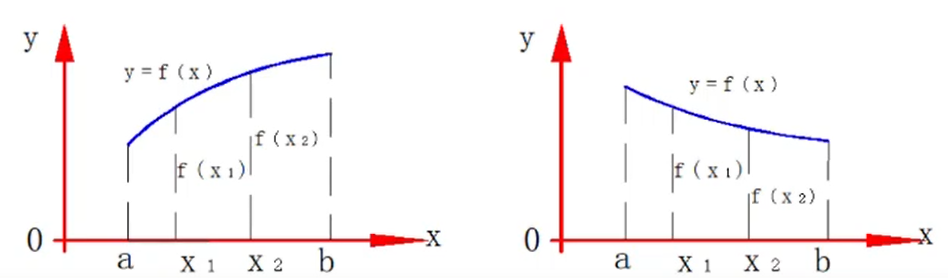
- 单调性：
02. 极限
03. 无穷大与无穷小
04. 连续性与导数
05. 偏导数
06. 方向导数
07. 梯度
若有收获，就点个赞吧
0 人点赞
