01. 集合的基本概念

1.1 集合的介绍

  • 集合的概念：
    • 在数学中就有集合，是指把一定范围的、确定的、可区分的事物当成一个整体，这个整体就称之为集合。
    • 集合中的各个事物就称为集合的元素。
  • 集合的特性：
    • 无序性：集合中每个元素的地位是相同的，不像列表等中的元素有先来后到一说，因此集合无法被索引切片。
    • 互异性：任意两个元素之间不能相同，即同一个元素在一个集合中只能出现一次。
    • 确定性：给定一个集合和一个元素，那么这个元素与集合的关系就是确定的，要么属于，要么不属于。

  • Python中集合的概念与数学中的集合是基本一致的，并且Python中的集合是一个可变的无序序列。

    1.2 集合的定义

    1.2.1 字面量{}定义法

  • 集合由一个大括号包裹，元素用逗号隔开；集合定义时元素的顺序和打印出来的顺序大概率是不相同的。 ```python s = {10, 20, 30, 40} print(s, type(s)) # {40, 10, 20, 30}

在定义时若集合中有相同的元素，则最后也只会保留其中一个。

s = {10, 20, 20, 30, 40, 10, 40, 10} print(s) # {40, 10, 20, 30}

  2. - 这种方式不能定义空集合，因为`{}`会被Python认为是一个空字典。
  3. ```python
  4. s = {}
  5. print(s, type(s))  # {} <class 'dict'>

1.2.2 set()函数构建集合

  • 使用s = set(seq)函数可以将序列seq构造成集合。 ```python set1 = set(“Hello”) # 通过字符串构造 print(set1) # {‘e’, ‘l’, ‘o’, ‘H’}，重复的l只保留了一个，并且顺序是乱的。

set2 = set([12, 31, 53, 43, 51]) # 通过列表构造 print(set2) # {43, 12, 51, 53, 31}

set3 = set(range(1, 10)) # 通过range()序列构造 print(set3) # {1, 2, 3, 4, 5, 6, 7, 8, 9}

  2. - 使用`set()`函数可以构建一个空集合，也是构建空集合的唯一方式。
  3. ```python
  4. s = set()
  5. print(s, type(s))  # set() <class 'set'>

02. 集合的相关操作

2.1 集合的运算

2.1.1 &交际、|并集、^对称差集、-差集

  • s3 = s1 & s2：&用于求s1和s2的交集，并将结果赋值给s3。
    • 所谓交集，就是取两个集合中共同部分的数据组成的集合，图解为：

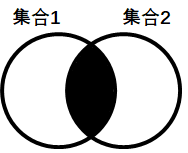
image.png

  • 代码实现交集计算：
    1. s1 = {18, 30, 28, 38, 45}
    2. s2 = {20, 30, 45, 56, 71}
    3. s3 = s1 & s2
    4. print(s3)  # {45, 30}
  • s3 = s1 | s2：|用于求s1和s2的并集，并将结果赋值给s3。
    • 所谓并集，就是将两个集合中的所有元素都取出来，然后构成一个集合。

image.png

  • 代码实现并集计算：
    1. s1 = {18, 30, 28, 38, 45}
    2. s2 = {20, 30, 45, 56, 71}
    3. s3 = s1 | s2
    4. print(s3)  # {38, 71, 45, 18, 20, 56, 28, 30}
  • s3 = s1 ^ s2：^用于求s1和s2的对称差集，并将结果赋值给s3。
    • 所谓对称差集，就是并集 - 交集。

image.png


  • 代码实现对称差集计算：
    1. s1 = {18, 30, 28, 38, 45}
    2. s2 = {20, 30, 45, 56, 71}
    3. s3 = s1 ^ s2
    4. print(s3)  # {18, 20, 38, 71, 56, 28}
  • s3 = s1 - s2：-用于求s1和s2的差集，并将结果赋值给s3。
    • 所谓差集，就是并集 - 集合2，也可以理解成取对称集中的前半部分，还可以理解成集合1 - 交集。

image.png

  • 代码实现差集计算：
    1. s1 = {18, 30, 28, 38, 45}
    2. s2 = {20, 30, 45, 56, 71}
    3. s3 = s1 - s2
    4. print(s3)  # {18, 28, 38}

    2.1.2 复合赋值运算符

  • 针对于2.1.1中的运算符，都有对应的复合赋值运算符。 ```python s1 = {18, 30, 28, 38, 45} s2 = {20, 30, 45, 56, 71} s1 &= s2 print(s1) # {45, 30}

s1 |= s2 print(s1) # {20, 71, 56, 45, 30}

s1 -= s2 print(s1) # set()

s1 ^= s2 print(s1) # {71, 45, 20, 56, 30}

  2. - 2.1.1中的运算符不会影响集合s1和集合s2，但2.1.2中的运算符会影响集合s1，它是直接操作于s1之上的。
  3. <a name="hwFoS"></a>
  4. #### 2.1.3 比较运算符
  6. - `s1 == s2`：判断集合s1与集合s2是否相同。
  7. ```python
  8. s1 = {18, 30, 28, 38, 45}
  9. s2 = {20, 30, 45, 56, 71}
  10. s3 = {18, 30, 28, 38, 45}
  11. print(s1 == s2)  # False
  12. print(s1 == s3)  # True

  • s1 != s2：判断集合s1与集合s2是否不同。

    1. s1 = {18, 30, 28, 38, 45}
    2. s2 = {20, 30, 45, 56, 71}
    3. s3 = {18, 30, 28, 38, 45}
    4. print(s1 != s2)  # True
    5. print(s1 != s3)  # False

    2.1.4 子集与超集运算

  • 子集与超集：若集合A中的任意一个元素集合B中都有，那么称集合A是集合B的子集，集合B是集合A的超集。

    • 真子集：若集合A是集合B的子集，但集合A与集合B并不相等，则称集合A是集合B的真子集。
    • 子集 = 真子集 + 集合本身 + 空集。

  • s1 > s2：判断s2是否为s1的真子集。

    1. s1 = {18, 30, 28, 38, 45}
    2. s2 = {30, 45, 18}
    3. s3 = {18, 30, 28, 38, 45}
    4. print(s1 > s2)  # True
    5. print(s1 > s3)  # False

  • s1 >= s2：判断s2是否为s1的子集。

    1. s1 = {18, 30, 28, 38, 45}
    2. s2 = {30, 45, 18}
    3. s3 = {18, 30, 28, 38, 45}
    4. print(s1 >= s2)  # True
    5. print(s1 >= s3)  # True

  • 同样的道理，s1 < s2用于判断s1是否为s2的真子集；s1 <= s2用于判断s1是否为s2的子集。

    1. s1 = {30, 45, 18}
    2. s2 = {18, 30, 28, 38, 45}
    3. print(s1 < s2)  # True
    4. print(s1 <= s2)  # True

    2.1.5 in、not in成员运算符

  • ele in s：判断元素ele是否是集合s中的元素。

    1. s = {18, 30, 28, 38, 45}
    2. print(18 in s)  # True
    3. print(71 in s)  # False

  • ele not in s：判断元素ele是否不是集合s中的元素。

    1. s = {18, 30, 28, 38, 45}
    2. print(18 not in s)  # False
    3. print(71 not in s)  # True

    2.2 集合的遍历

  • 由于集合是无需序列没有索引，因此不能通过索引遍历元素，也不能用enumerate枚举了。

  • 故元组只能通过for-in直接遍历。

    1. s = {12, 34, 56, 78}
    2. for i in s:
    3.   print(i)

    2.3 集合的增删函数

    2.3.1 add()添加元素

  • s.add(obj)：用于将元素obj添加到集合s中。

    1. s = {12, 34, 56, 71, 29}
    2. s.add(30)
    3. print(s)  # {34, 71, 56, 12, 29, 30}

  • 如果元素已存在，则此操作无效。

    1. s = {12, 34, 56, 71, 29}
    2. s.add(34)
    3. print(s)  # {34, 71, 56, 12, 29}，依旧是原来那些数据。

    2.3.2 remove()删除元素

  • s.remove(obj)：用于将元素obj从集合s中删除。

    1. s = {12, 34, 56, 71, 29}
    2. s.remove(56)
    3. print(s)  # {34, 71, 12, 29}

  • 若元素obj不存在于集合s中，则会报错。

    1. s = {12, 34, 56, 71, 29}
    2. s.remove(83)  # KeyError: 83

    2.3.3 discard()删除元素

  • s.discard(obj)：与s.remove(obj)一样，也用于将元素obj从集合s中删除。

    1. s = {12, 34, 56, 71, 29}
    2. s.discard(56)
    3. print(s)  # {34, 71, 12, 29}

  • 与remove()函数最大的不同在于若元素obj不存在于集合s中，discard()函数不会报错。

    1. s = {12, 34, 56, 71, 29}
    2. s.discard(83)

    2.3.4 clear()清空集合

  • s.clear()：会将集合s中的所有元素 全部删除，让集合s变成一个空集合。

    1. s = {12, 34, 56, 71, 29}
    2. s.clear()
    3. print(s)  # set()

    2.3.5 pop()随机删除一个元素

  • s.pop()：会随机删除集合s中的任意一个元素。

    1. s = {12, 34, 56, 71, 29}
    2. s.pop()
    3. print(s)

  • 但是若集合s已经是一个空集合了，那么在运行pop()函数则会报错。

    1. s = set()
    2. s.pop()  # KeyError: 'pop from an empty set'

  • pop()删除的随机性分析：

    • 集合虽然是个无序序列，但是实际上它还是有序的，这从每次打印的结果可以看出来。
    • 虽然打印出来的数据顺序和集合定义时数据的顺序不一样，但是多运行几次就会发现，每次打印出来的结果是一样的。
    • 这就说明集合在计算前会通过其内部的算法将数据顺序重新进行排序，而排序的结果是确定的。
    • pop()虽说是随机删除一个数据，但实际上它删除的永远是经过排序的集合中的第一个元素。
      1. s = {12, 34, 56, 71, 29}
      2. print(s)  # {34, 71, 56, 12, 29}，每次运行都是这个结果，说明集合实际上是有序的。
      3. s.pop()
      4. print(s)  # {71, 56, 12, 29}，每次删除的都是排序后集合中的第一个元素34，说明pop()并不是随机删除元素。

      2.3.6 copy()拷贝集合

  • s2 = s1.copy()可以将集合s1中的元素拷贝一份给s1。

  • 但是s1和s2在内存中的地址是不一样的，这在列表的深浅拷贝中有介绍过。

    1. s1 = {12, 34, 56, 71, 29}
    2. s2 = s1.copy()
    3. print(s1, id(s1))  # {34, 71, 56, 12, 29} 2114184720160
    4. print(s2, id(s2))  # {34, 71, 56, 12, 29} 2113768597536

    2.4 集合的运算函数

    2.4.1 求交集intersection()/intersection_update()

  • s1.intersection(s2)用于求集合s1与集合s2的交集，等价于s1 & s2

    1. s1 = {18, 30, 28, 38, 45}
    2. s2 = {20, 30, 45, 56, 71}
    3. s3 = s1.intersection(s2)
    4. print(s3)  # {45, 30}

  • s1.intersection_update(s2)也用于求集合s1与集合s2的交集，等价于s1 &= s2

    1. s1 = {18, 30, 28, 38, 45}
    2. s2 = {20, 30, 45, 56, 71}
    3. s1.intersection_update(s2)
    4. print(s1)  # {45, 30}

    2.4.2 求并集union()/update()

  • s1.union(s2)用于求集合s1与集合s2的并集，等价于s1 | s2

    1. s1 = {18, 30, 28, 38, 45}
    2. s2 = {20, 30, 45, 56, 71}
    3. s3 = s1.union(s2)
    4. print(s3)  # {38, 71, 45, 18, 20, 56, 28, 30}

  • s1.update(s2)也用于求集合s1与集合s2的并集，等价于s1 |= s2

    1. s1 = {18, 30, 28, 38, 45}
    2. s2 = {20, 30, 45, 56, 71}
    3. s1.update(s2)
    4. print(s1)  # {38, 71, 45, 18, 20, 56, 28, 30}

    2.4.3 求对称差集symmetric_difference()/symmetric_difference_update()

  • s1.symmetric_difference(s2)用于求集合s1与集合s2的对称差集，等价于s1 ^ s2

    1. s1 = {18, 30, 28, 38, 45}
    2. s2 = {20, 30, 45, 56, 71}
    3. s3 = s1.symmetric_difference(s2)
    4. print(s3)  # {18, 20, 38, 71, 56, 28}

  • s1.symmetric_difference_update(s2)也用于求集合s1与集合s2的对称差集，等价于s1 ^= s2

    1. s1 = {18, 30, 28, 38, 45}
    2. s2 = {20, 30, 45, 56, 71}
    3. s1.symmetric_difference_update(s2)
    4. print(s1)  # {18, 20, 38, 71, 56, 28}

    2.4.4 求差集difference()/difference_update()

  • s1.difference(s2)用于求集合s1与集合s2的差集，等价于s1 - s2

    1. s1 = {18, 30, 28, 38, 45}
    2. s2 = {20, 30, 45, 56, 71}
    3. s3 = s1.difference(s2)
    4. print(s3)  # {18, 28, 38}

  • s1.difference_update(s2)也用于求集合s1与集合s2的差集，等价于s1 -= s2

    1. s1 = {18, 30, 28, 38, 45}
    2. s2 = {20, 30, 45, 56, 71}
    3. s1.difference_update(s2)
    4. print(s1)  # {18, 38, 28}

    2.5 集合的判断函数

    2.5.1 issubset()判断子集

  • s1.issubset(s2)用于判断集合s1是否是s2的子集，等价于s1 <= s2

    1. s1 = {18, 30, 28, 38, 45}
    2. s2 = {30, 45, 18}
    3. print(s1.issubset(s2))  # False
    4. print(s2.issubset(s1))  # True

    2.5.2 issupperset()判断超集

  • s1.issupperset(s2)用于判断集合s1是否是s2的超集，等价于s1 >= s2

    1. s1 = {18, 30, 28, 38, 45}
    2. s2 = {30, 45, 18}
    3. print(s1.issuperset(s2))  # True
    4. print(s2.issuperset(s1))  # False

    2.5.3 isdisjoint()判断两个集合是否有交集

  • s1.isdisjoint(s2)用于判断集合s1和集合s2的交集是否为空，即判断二者是否有交集。

    • 若s1和s2的交集为空集，则isdisjoint()函数返回True，即二者没有交集。

      1. s1 = {18, 30, 28, 38, 45}
      2. s2 = {20, 30, 45, 56, 71}
      3. print(s1 & s2)  # {45, 30}
      4. print(s1.isdisjoint(s2))  # False

    • 若s1和s2的交集不为空集，则isdisjoint()函数返回False，即二者有交集。

      1. s1 = {18, 30, 28, 38, 45}
      2. s2 = {20, 22, 54, 56, 71}
      3. print(s1 & s2)  # set()
      4. print(s1.isdisjoint(s2))  # True

      03. 不可变集合

      3.1 不可变集合的介绍与构建

  • 不可变集合frozenset是一个不可更改元素的集合，frozenset与set的关系类似于list与tuple的关系。

  • 不可变集合只能通过frozenset()函数来构造： ```python

    构造空集合

    s = frozenset() print(s) # frozenset()

构造普通集合

s = frozenset({1, 3, 5, 7, 9}) print(s) # frozenset({1, 3, 5, 7, 9})

通过range()序列构造集合

s = frozenset(range(1, 101, 10)) print(s) # frozenset({1, 71, 41, 11, 81, 51, 21, 91, 61, 31})

  1. <a name="SxQN5"></a>
  2. ### 3.2 不可变集合的运算
  4. - frozenset()不可变集合可以使用2.1 集合的运算中所有的运算符。
  5. - 交集、并集、对称差集、差集：
  6. ```python
  7. s1 = frozenset(range(1, 101, 10))
  8. s2 = frozenset(range(1, 81, 10))
  9. print(s1 & s2)  # frozenset({1, 71, 41, 11, 51, 21, 61, 31})
  10. print(s1 | s2)  # frozenset({1, 71, 41, 11, 81, 51, 21, 91, 61, 31})
  11. print(s1 ^ s2)  # frozenset({81, 91})
  12. print(s1 - s2)  # frozenset({81, 91})

  • 复合赋值运算符：frozenset()不可变集合虽然可以使用所有的复合赋值运算符，但与普通set集合有本质差别。

    1. s1 = frozenset(range(1, 101, 10))
    2. s2 = frozenset(range(1, 81, 10))
    3. s1 &= s2
    4. print(s1)  # frozenset({1, 71, 41, 11, 51, 21, 61, 31})
    • frozenset()是一个不可变的序列，虽然frozenset可以执行复合赋值运算符的操作，但它操作的不是运算符前面的变量的空间，而是将运算结果重新开辟一块空间，再把变量指针指向新的地址。 ```python s1 = frozenset(range(1, 101, 10)) s2 = frozenset(range(1, 81, 10)) print(id(s1)) # 2198778851104 s1 |= s2 print(s1) # frozenset({1, 71, 41, 11, 81, 51, 21, 91, 61, 31}) print(id(s1)) # 2198779017248，地址发生了改变

可变集合（即普通set集合）做这种运算就不会改变地址。

s1 = set(range(1, 101, 10)) s2 = set(range(1, 81, 10)) print(id(s1)) # 2884759109408 s1 &= s2 print(id(s1)) # 2884759109408 ```

  • 其他运算符的操作都与普通set集合没有什么差别。