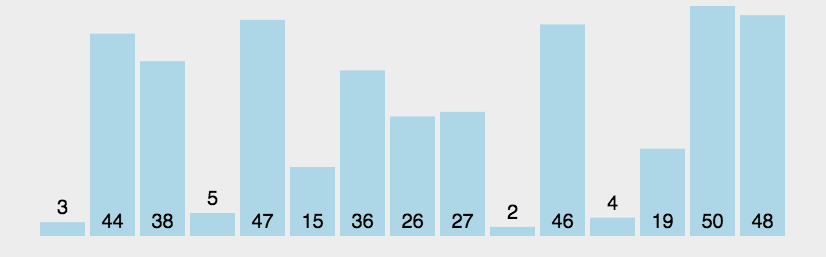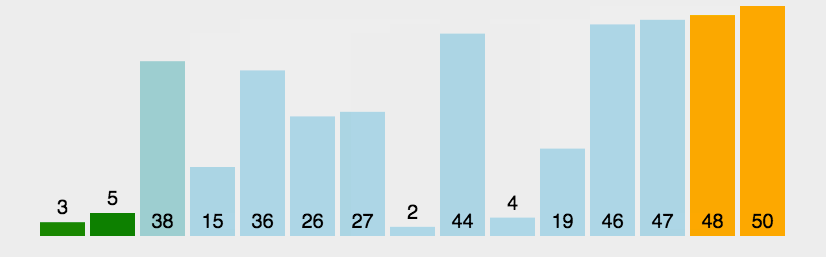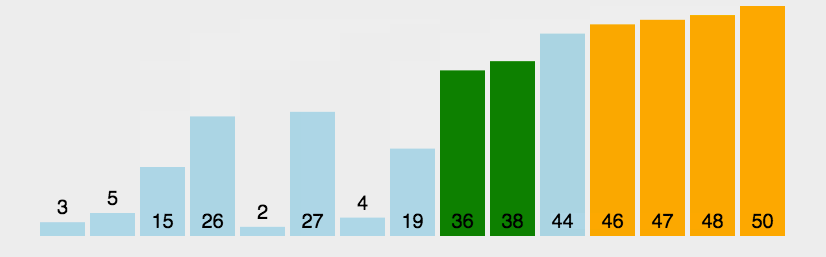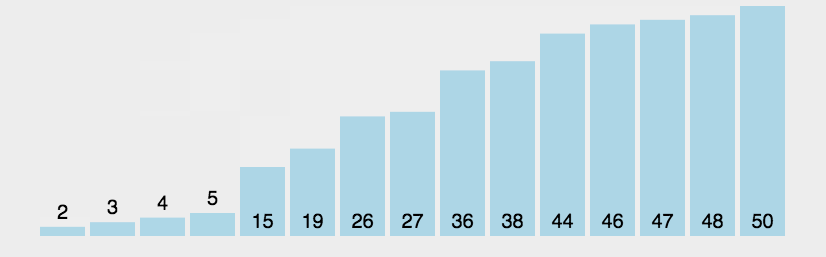01. 冒泡排序

1.1 冒泡排序思想

  • 冒泡排序是一种简单的排序算法。
  • 它重复地走访过要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。
  • 走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。

  • 这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

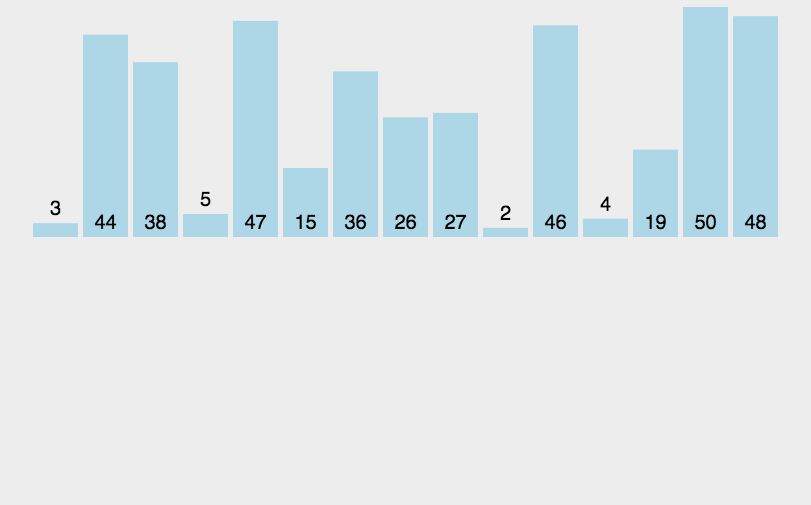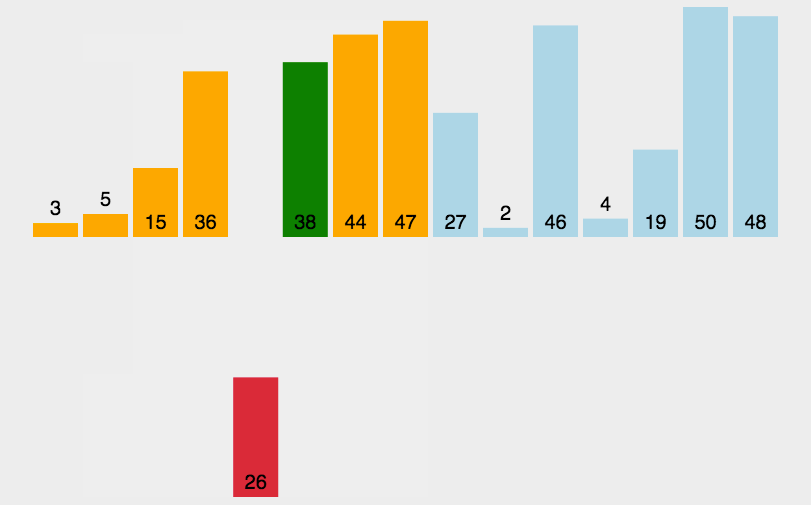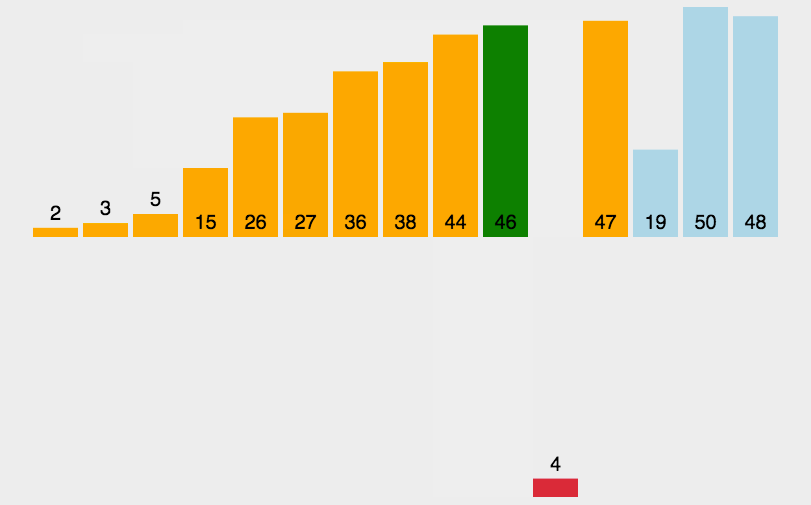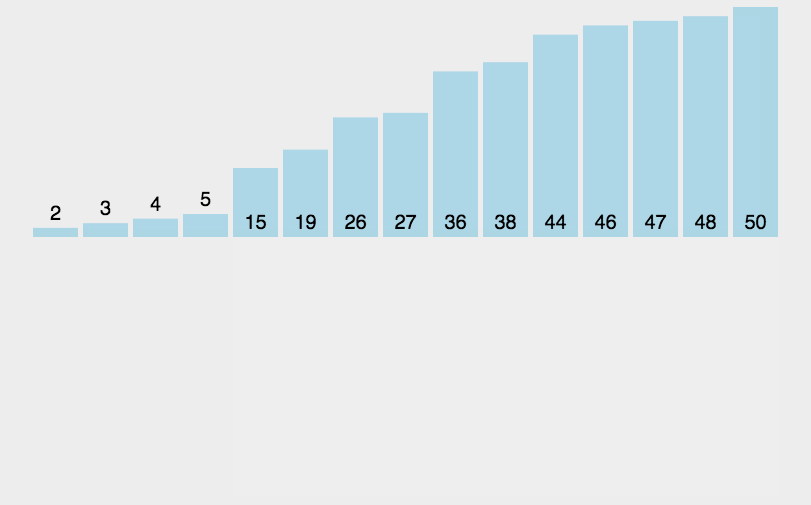
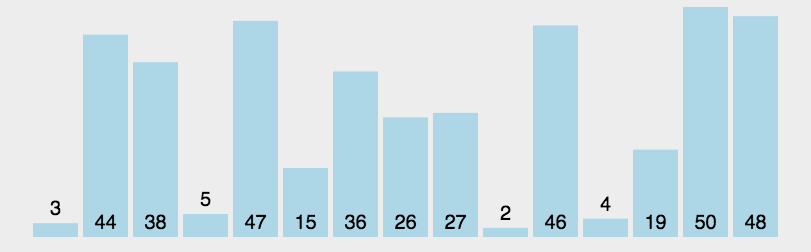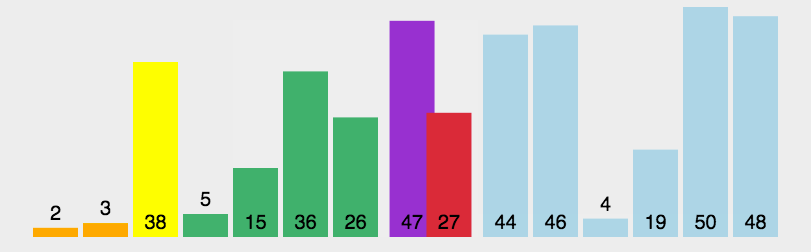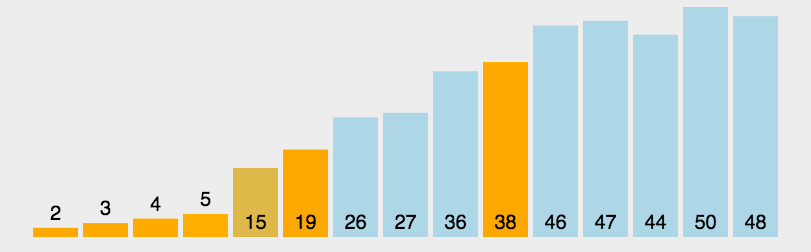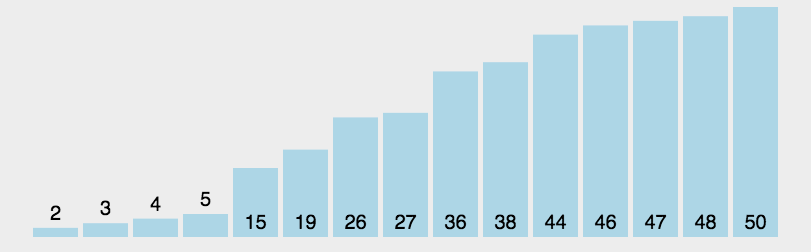
    1.2 图解冒泡排序

  • 比较相邻的元素。如果第一个比第二个大，就交换它们两个；

  • 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样在最后的元素应该会是最大的数；
  • 针对所有的元素重复以上的步骤，除了最后一个；
  • 重复步骤1~3，直到排序完成。

03. 排序算法 - 图1

1.3 冒泡排序的代码实现

  • 拿元素进行比较的这个操作就是遍历操作（遍历操作就是一个循环结构），并且遍历的次数也要重复多次，因此需要嵌套循环结构才能完成这项功能。
  • 嵌套循环就分为内层循环和外层循环，其中：
    • 内层循环：每次从索引为0的位置开始，获取要进行排序的元素，并与下一个元素进行比较。
    • 外层循环：控制的是排序时遍历的操作要被重复的次数。
  • 循环次数：
    • 外层循环：若对整个列表排序，则重复次数为：03. 排序算法 - 图2，故外层循环03. 排序算法 - 图3。
    • 内层循环：内层循环的次数，实际上就是相邻元素两两比较的次数。对于一个长度为6的列表而言，一些数据如下：

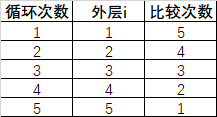
1661395639939.jpg

  • 由此可以得出，内层循环03. 排序算法 - 图5。
    • 结合上述知识点，编码实现对列表lst = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]的升序排序。
      1. lst = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]
      2. for i in range(1, len(lst)):
      3. for j in range(len(lst) - i):
      4.  # 若当前元素比下一位元素大，则交换两个元素的位置，否则当前什么也不做，并进行下一次循环。
      5.  if lst[j] > lst[j + 1]:
      6.      lst[j], lst[j + 1] = lst[j + 1], lst[j]
      7. print(lst)  # [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

      02. 选择排序

      2.1 选择排序思想

  • 选择排序(Selection Sort)是一种简单直观的排序算法。

  • 它的工作原理：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

    2.2 图解选择排序

  • 第一次固定第一个位置，将这个位置的元素视为列表中最小的元素，然后依次与之后的元素进行比较。

  • 若在与之后的元素比较的过程中，发现了比第一个元素还要小的元素，则将该元素进行标记，并用该元素与之后的元素继续进行比较，这样一趟下来就可以发现数列中为排序部分中最小的那个元素，将该元素与第一个位置的元素交换位置。
  • 接着固定第二个位置的元素，将这个位置的元素看成第二小的元素，然后重复步骤2，直到找出第二小的元素后，与第二个位置的元素交换位置。
  • 接着再固定第三个元素，以此类推，直到排序完成。

03. 排序算法 - 图6

2.3 选择排序的代码实现

  • 插入排序也需要用双层嵌套循环才能完成工作。
  • 外层循环
    • 控制遍历操作的次数，排序整个数组时，需遍历列表长度-1次。
    • 通过分析下表，可以得出外层循环的次数等于固定元素的索引 + 1，因此可以若要把外层循环遍历i与固定元素的索引联系起来，则03. 排序算法 - 图7

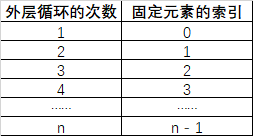
1661432185980.jpg

  • 故外层循环可以定义为for i in range(0, len(lst) - 1)，并且每次固定元素为lst[i]，最开始认为最小的元素的下标min_index = i。
    • 内层循环：
  • 内层循环用于从固定元素之后的那个元素开始，一直遍历到列表末尾，因此内层循环可以定义为for j in range(i + 1, len(lst))
  • 在循环过程中，若找到了比固定位置元素小的元素，不要着急交换位置，因为它可能只是比固定位置的元素小，但非未排序列表中最小的元素。
  • 因此可以先记录这个元素的下标，并接着往后找，直到找到未排序列表中最小的元素（只有遍历完整个未排序列表才能确定）时，再交换位置。
  • 这样减少了不必要的交换位置的操作，可以增加程序的运行效率。
    • 结合上述知识点，编码实现对列表lst = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]的升序排序。
      1. lst = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]
      2. for i in range(len(lst) - 1):
      3. min_index = i  # 记录当前找到的未排序的数组中最小的元素的下标
      4. for j in range(i + 1, len(lst)):
      5.  if lst[j] < lst[min_index]:
      6.      min_index = j  # 若找到了比当前已知最小的元素还要小的元素，则记录下标。
      7. lst[i], lst[min_index] = lst[min_index], lst[i]  # 将找到的最小元素与当前固定位置上的元素交换。
      8. print(lst)  # [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

      03. 插入排序

      3.1 插入排序思想

  • 插入排序（Insertion-Sort）的算法描述是一种简单直观的排序算法。

  • 它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

    3.2 图解插入排序

  • 从第一个元素开始，该元素可以认为已经被排序；

  • 取出下一个元素，在已经排序的元素序列中从后向前扫描；
  • 如果该元素（已排序）大于新元素，将该元素移到下一位置；
  • 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置；
  • 将新元素插入到该位置后；
  • 重复步骤2~5。

03. 排序算法 - 图9

3.3 插入排序的代码实现

  • 插入排序也需要用双层嵌套循环才能完成工作。
  • 外层循环：
    • 控制遍历操作的次数，排序整个数组时，需遍历列表长度-1次。
    • 并且由于插入排序的扫描方式是从后往前扫描的，0索引位前面没有数据，因此插入排序是从下标为1的元素开始的。
    • 总结两点可以得出，03. 排序算法 - 图10。
  • 内层循环：用于获取元素并进行比较。
    • 第一次循环的起始下标为1，最坏情况结束位置下标为1。
    • 第二次循环的起始下标为2，最坏情况结束位置下标为1。
    • 第三次循环的起始下标为3，最坏情况结束位置下标为1。
    • ……
    • 第n次循环的起始下标为n，最坏情况结束位置下标为1。
    • 可以得出，内层遍历时元素的下标起始值与外层循环的次数是对应的，并且最坏情况结束位置下标都为1，是负方向上的遍历。
    • 由此可以得出，03. 排序算法 - 图11
  • 排序方式：
    • 若当前元素lst[j]比前一个元素lst[j - 1]小，则交换两个元素的位置，交换完成后继续向前一个元素比较。
    • 直到当前元素lst[j]比前一个元素lst[j - 1]大时，该元素排序完成。

  • 结合上述知识点，编码实现对列表lst = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]的升序排序。

    1. lst = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]
    2. for i in range(1, len(lst)):
    3.   for j in range(i, 0, -1):
    4.       if lst[j] < lst[j - 1]:
    5.           lst[j], lst[j - 1] = lst[j - 1], lst[j]
    6.       else:
    7.           # 当lst[j] >= lst[j - 1]时，就不需要交换位置了。
    8.           # 在当前位置之前的元素也一定是大于lst[j - 1]的。
    9.           # 因此当前循环到这里时，就可以结束了。
    10.           break
    11. print(lst)  # [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

    04. 快速排序

    4.1 快速排序思想

  • 快速排序实际上是对冒泡排序的一种改进，采用递归实现对列表的排序。

  • 快速排序通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小。

  • 然后分别对这两部分记录继续进行排序（在这里用递归），以达到整个序列有序。

    4.2 图解快速排序

    4.2.1 快速排序基本实现思路

  • 快速排序使用分治法来把一个串（list）分为两个子串（sub-lists）。

  • 首先从数列中挑出一个元素（一般为序列中的第一个元素），称为 “基准”（pivot）；
  • 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。
  • 在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
  • 递归的把小于基准值元素的子数列和大于基准值元素的子数列排序。

03. 排序算法 - 图12

4.2.2 快速排序的简单示例

  • 一般而言基准值都是找序列中的第一个元素，以nums = [27, 22, 19, 41, 33, 24, 56]为例。
  • 第一次排序：基准值=27
    • 比基准值小的：22、19、24
    • 比基准值大的：41、33、56
    • 序列：nums = [22, 19, 24, 27, 41, 33, 56]
  • 第二次排序：
    • 小的子列sub_small = [22, 19, 24]：基准值22，比基准值小的：19，比基准值大的24，子序列：sub_small = [19, 22, 24]，排序完成。
    • 大的子列sub_big = [41, 33, 56]：基准值41，比基准值小的：33，比基准值大的56，子序列：sub_big = [33, 41, 56]，排序完成。
  • 最终序列：nums = [19, 22, 24, 27, 33, 41, 56]

    4.3 快速排序的代码实现

    ```python def quick_sort(lst): if len(lst) <= 1:
    1.   # 没有元素或者只有一个元素时（即没有可对比的数据时，递归结束）
    2.   return lst
    else:
    1.   # 当列表长度大于等于1时，就要开始排序
    2.   pivot = lst[0]  # 基准值
    3.   small = []  # 存放比基准值小的数据
    4.   big = []  # 存放比基准值大的数据
    5.   for ele in lst[1:]:  # 基准值元素不用和自身比较，因此直接从索引为1的元素开始即可。
    6.       if ele >= pivot:
    7.           big.append(ele)
    8.       else:
    9.           small.append(ele)
    10.   # 因为此时的small和big还是乱序的，因此还要对small和big进行同样的排序操作（递归）。
    11.   # 将排好序的small和big与基准值拼在一起，然后该结果就是排序的返回值了（即排完序的列表）。
    12.   return quick_sort(small) + [pivot] + quick_sort(big)  # 这里做的是列表的拼接操作，因此pivot要加上中括号，代表一个列表。

lst = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48] sorted_lst = quick_sort(lst) print(sorted_lst) # [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

nums = [27, 22, 19, 41, 33, 24, 56] sorted_nums = quick_sort(nums) print(sorted_nums) # [19, 22, 24, 27, 33, 41, 56] ```