01. 统计学前置知识

01. 五个基本数字

1.1 均值

• 均值也就是平均数（mean），有时候也称为算数平均数，用于测量集中趋势。
• 均值的求法：先将所有数字加起来，然后除以数字的个数。
• 求数据的均值：23、29、20、32、23、21、33、25。

1.2 中位数

• 所谓中位数（median）就是选取中间的数，是测量集中趋势的另一种方式。
• 中位数的求法：先将数据从小到大排序，若奇数个数据，则最中间的数据就是中位数；若偶数个数据，则取出最中间的两个数据求平均。
• 求数据的中位数：23、29、20、32、23、21、33、25。

1.3 众数

• 众数（mode）也就是数据集中出现频率最多的数字。

• 数据23、29、20、32、23、21、33、25的众数为

  1.4 极差

• 极差（range）指的是这些数字分开得有多远。

• 极差的求法：
  • 用一组数据中最大的数减去这组数据中最小的数。
  • 极差越大，表示这些数字之间分的越开，即最大数和最小数之间的差就越大；极差越小，数字之间就越紧密。
• 求数据65、81、73、85、94、79、67、83、82的极差：

1.5 中程数

• 中程数（mid-range）是考虑数值中间值的又一种方式。
• 中程数的求法：取最大数和最小数的平均值。
• 求数据65、81、73、85、94、79、67、83、82的中程数。

02. 数据图表

2.1 象形统计图

• 象形统计图（pictograph）是用象形图像表示数据的一种方式。
• 根据如下象形统计图，计算多少调查对象具有O+型血，多少调查对象具有O-型血。

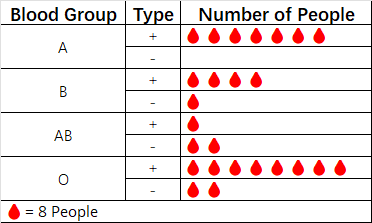
• 因为一个🩸代表了8个人，因此：

• 由此可以得出结论：64人具有O+型血，16人具有O-型血。

  2.2 条形图

• 条形图的基本概念：

  • 条形图（bar chart）是用宽度相同的条形的高度或长短来表示数据多少的图形。
  • 一个条形图中可以有多组颜色不同的图形，用于表示多组数据。
  • 条形图可以横置或纵置，纵置时也称之为柱状图（column chart）。
  • 一般来说，条形图适用于将事物归类统计，看看每一类事物分别是怎么样的情况。
• 根据下图数据，计算出哪个学生从期中考试到期末考试分数进步最大。

• 首先，从趋势上看，Jeff和Matra的图形是呈下降趋势的，由此这两个实际上是退步的。

• 接着，Jasmine和Nevin的上升趋势较低，只有Alejandra的上升趋势最明显，由此认为Alejandra的进步最大。

  2.3 线型图

  2.3.1 线型图的基本认识

• 线型图（line graph）又称点状图（point chart），用锚点表示数据，然后将数据之间用直线连接起来。

  • 将锚点用线连接起来是为了更好地看出趋势。
  • 线型图常用于表示随时间趋势变化的事物。（也可以是一个变量对另一个变量的趋势，并不一定只有时间）
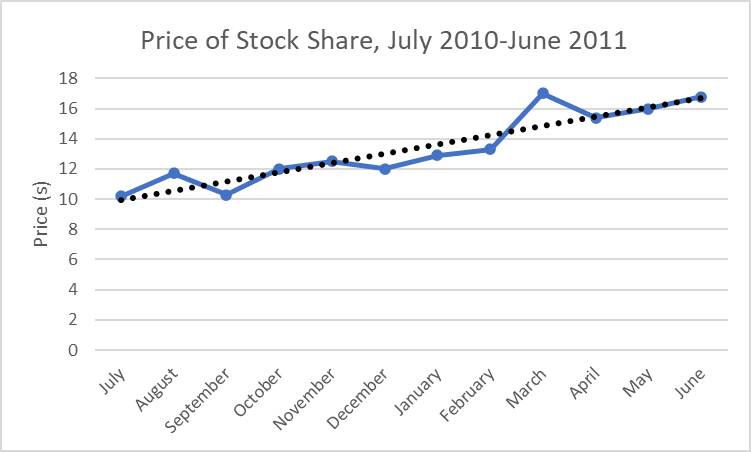
• 下表是一家投资公司2010年7月到2011年六月这12个月的特定股票业绩数据，其中横轴显示的是每个月，纵轴是该月对应的价格。

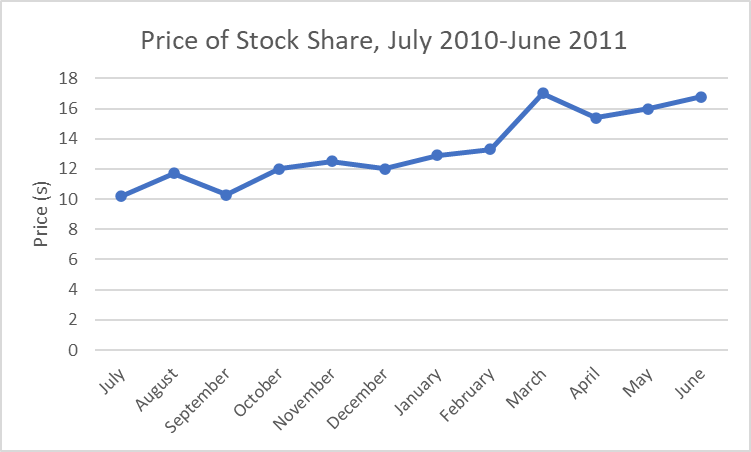
• 问，在这一年间，股票是上涨、下跌，还是不变。
  • 从每个月的趋势上看，每个月有涨有跌。（201007~201008：涨、201008~201009：跌、201009~201010：涨、201010~201011：涨、201011~201012：跌、201012~201101：涨、201101~201102：涨、201102~201103：涨、201103~201104：跌、201104~201105：涨、201105~201106：涨）
  • 但是从整体上看，2010年7月数据是$10.2，2011年6月是$16.8，总体是呈上升趋势的。

2.3.2 误导人的线型图

• 激动汽水雇了一家营销公司帮助促销其产品，对抗美味可乐。营销公司收集了以下关于消费者偏好的数据。

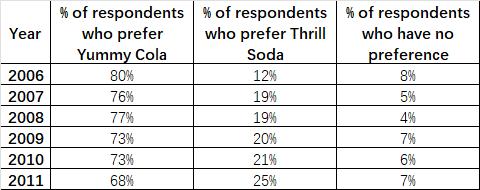
• 从数据上可以看出，喜欢美味可乐的人占比一直比喜欢激动汽水的高。但是营销公司给出以下两张线型图。

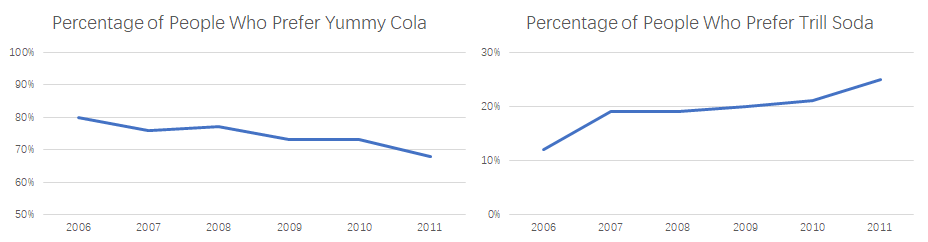
• 这两张线型图虽然都很诚实的展示两个品牌的数据情况。但是如果不看刻度，只看这两张图，就会产生误导：
  • 美味可乐的偏爱者百分比呈下降趋势，而激动汽水则呈上升趋势。
  • 若不看刻度，这两张图给人的感觉就是激动汽水的偏爱者人数不仅在上升，而且趋势要高于美味可乐。
  • 第二，由于激动汽水的最大值和最小值间距设置的较小，就给人一种激动趋势上升非常快速的错觉。
• 这两张图更好、更诚实的做法实际上是将两者绘制在一张图上，这样才能表现出最真实的效果。但是这样一来，所展现的效果就不是激动汽水希望看到的了。

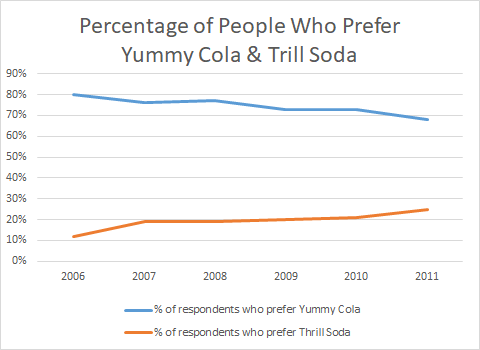
• 从这张图中可以看出，激动汽水实际上一直被美味可乐所压制着。通过刻度线的变化所表现出来的激动汽水的趋势要高于美味可乐不过是一个幻象罢了。

  2.4 饼图

• 饼图的基本概念：

  • 饼图（pie）由于像一块切开的饼而得名。
  • 饼图中的每一块小饼表示特定的部分占总额的百分比，占比越大，小饼的切块越大。
  • 所有小饼的百分数相加，结果一定为100%。
  • 饼图的作用可以总结为显示各部分的占比情况。
• 下图是一家旅行社过去一年的数据，记录了每个月地中海旅游项目的销售情况，求项目销售的最佳月和最差月。

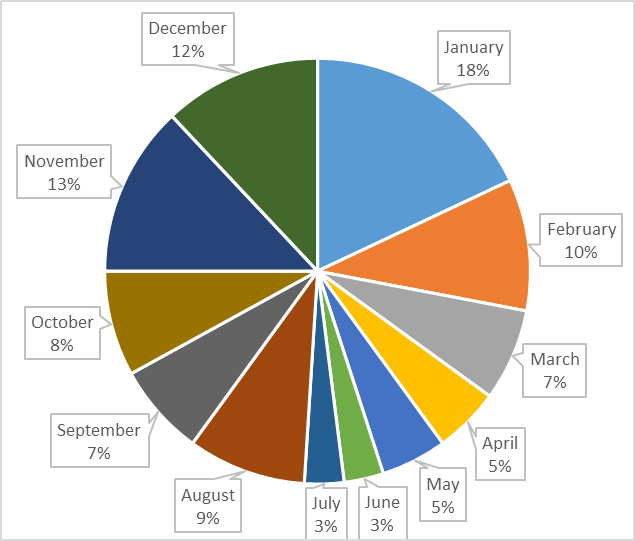
• 最佳月一定是销售占比最大的那个月，显然是一月份，占比18%；最差月是占比最少的那个月，是六月和七月，占比3%。

  2.5 茎叶图

• 茎叶图的基本概念：

  • 茎叶图（stem-and-leaf display）又称枝叶图，常用于展示分布情况。
  • 它的思路是将数组中的数按位数进行比较，将数的大小基本不变或者变化不大的位作为一个主干（茎）；将变化大的位数的数作为分枝（叶），并列在茎的后面。这样就可以清楚地看到每个主干后面的几个数，以及每个数具体是多少。
• 茎叶图最大的优势在于可以清楚的展示出数据的分布情况。
• 一位统计学者记录了一个篮球队中12名球员在一场比赛中的得分情况，然后用茎叶图来显示数据，问这个球队这场比赛共得了多少分。

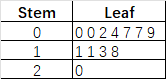
• 这张图中一共有0、1、2三个茎，这三个茎表示的是分数的十位数数字，即00~09、10~19、20~29三个大分支。后面的叶对应的是个位数数字。因此组合起来，这张图表示的数据是：
  • Stem 0：00、00、02、04、07、07、09。（Stem 0 (00~09)的数据分布比率是最高的）
  • Stem 1：11、11、13、18。
  • Stem 2：20。
• 因此这个球队这张比赛的总得分就是将三个茎上的所有叶加起来：

2.6 箱线图

2.6.1 箱线图的基本认识与绘制

• 箱线图（box-and-whiskers plot）常用于描述数据的散布情况和中位数。
• 一家餐厅的老板想知道他的顾客都来自何方，于是一天他决定收集数据统计顾客到餐厅的距离（单位：英里）。
• 最终得到的数据为：14、6、3、2、4、15、11、8、1、7、2、1、3、4、10、22、20。根据这组数据，画出箱线图。
  • 箱线图和中位数有关，因此第一步需要先给数据排序：1、1、2、2、3、3、4、4、6、7、8、10、11、14、15、20、22
  • 由此可以得到中位数：6，以及最大值：22和最小值：1。
  • 接着，中位数把这17个数字分成了小于Median的下半部分：1、1、2、2、3、3、4、4和大于Median的上半部分：7、8、10、11、14、15、20、22。找出下半部分的中位数（即总数据的下四分位数）为2.5和上半部分的中位数（即总数据的上四分位数）为12.5。
  • 此时数据就被下四分位数、中位数、上四分位数分成了四部分：

[1、2、2、2] q1:2.5 [3、3、4、4] median:6 [7、8、10、11] q2:12.5 [14、15、20、22]

• 作箱线图的第一步就是要显示所有数据的范围，因此第一步就是要把最小数据点和最大数据点标出来。

• 然后将下四分位数和上四分位数也在图上标出来，并且连成一个封闭的盒子。

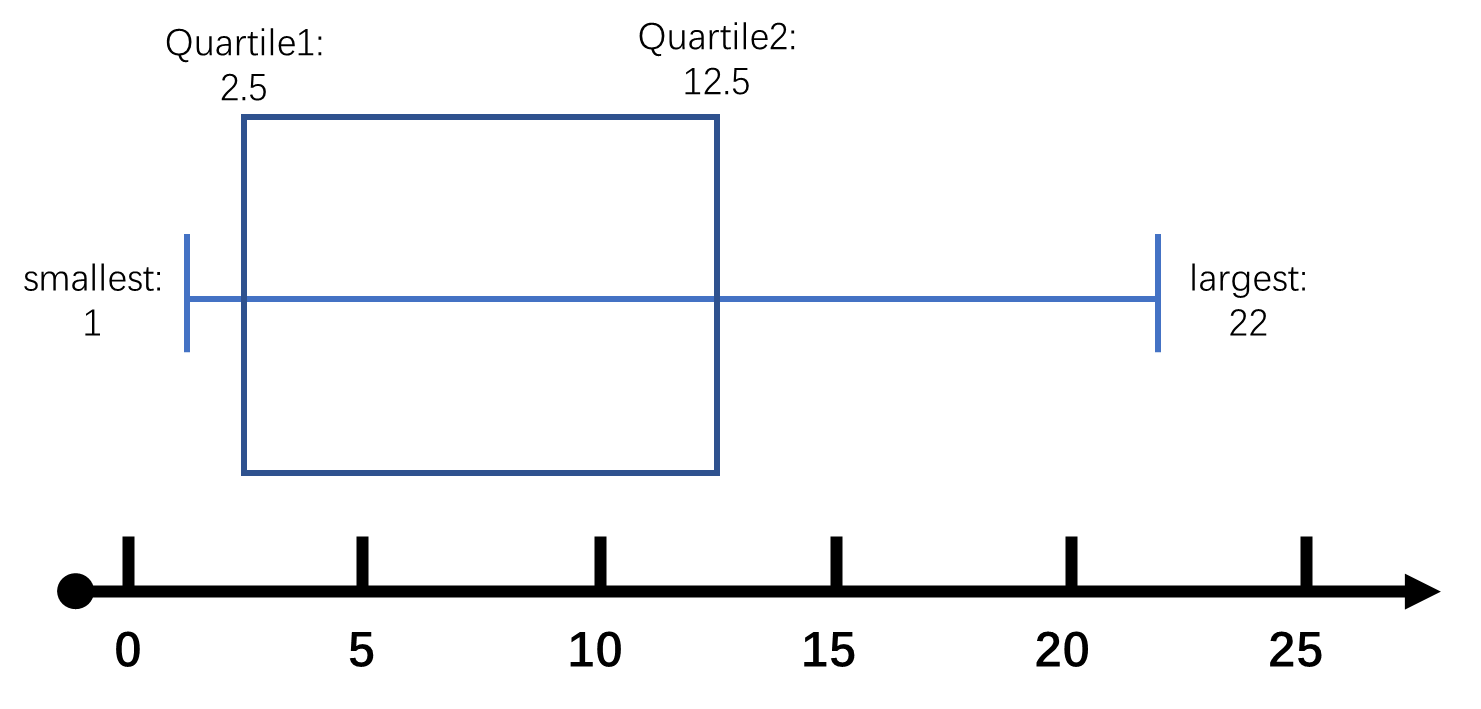
• 接着，将中位数也在盒子中标出来，然后将盒子的上半部分和下半部分都涂实。

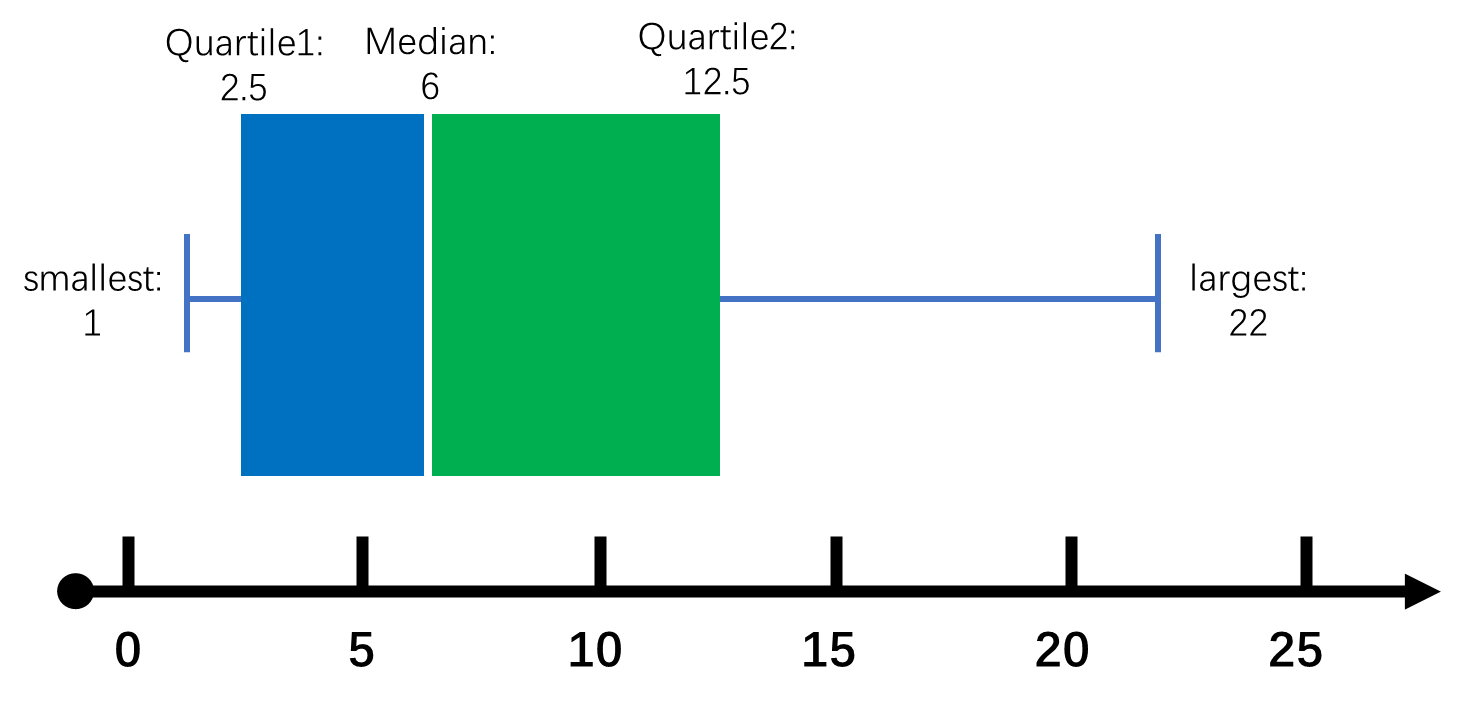
• 到此一个箱线图就画完了，但有时候，还可以在图上表示出数据的平均值。

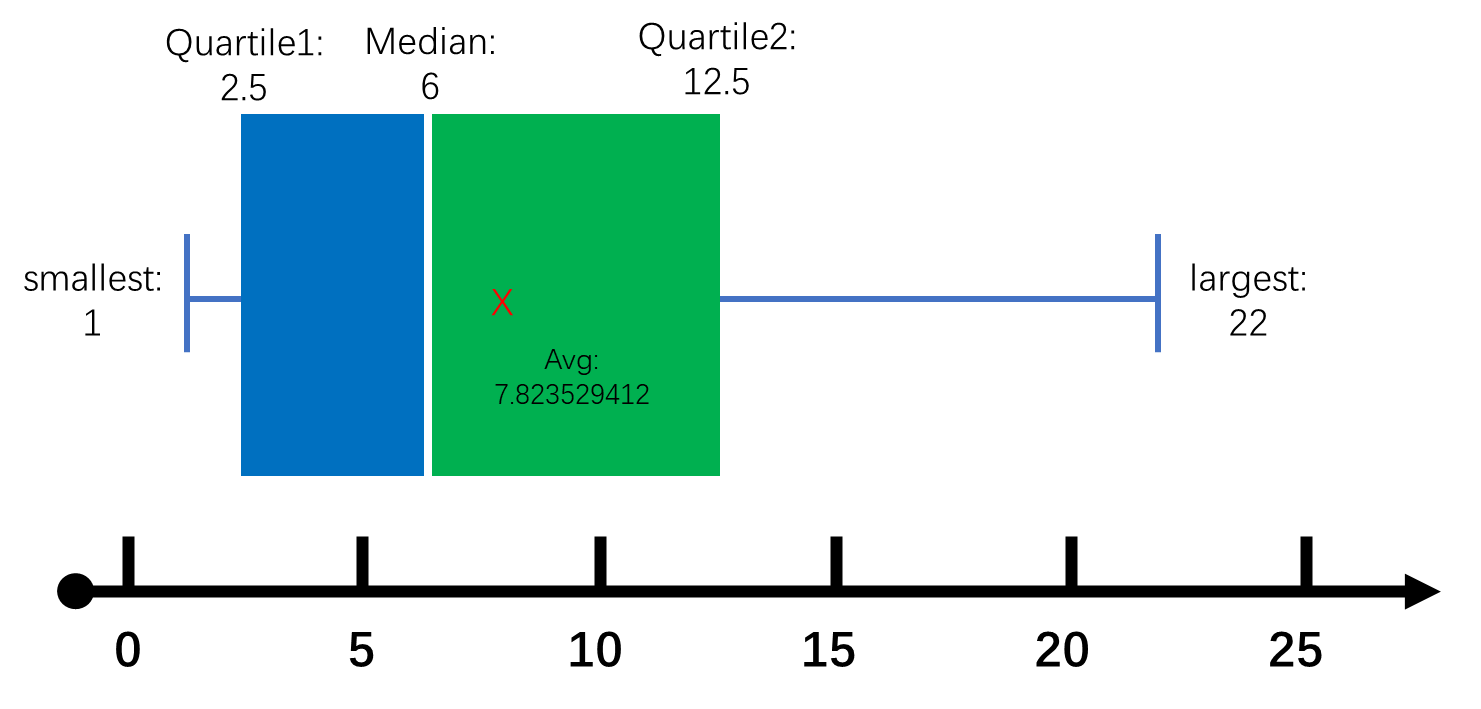
• 由此可以看出，一个箱线图所表示的信息有：

  • 中位数：6。
  • 下四分位数：2.5、上四分位数：12.5。
  • 中间一半的数据范围：2.5~12.5。
  • 所有顾客距离的散布情况：分布在1~22之间。

    2.6.2 从箱线图中看出信息

• 一位生态学家调查了当地大约100棵树的年龄，并绘制出以下箱线图。问，这些树年龄的极差是多少？这些树年龄的中位数是多少？这些树的四个年龄区间分别是多少？

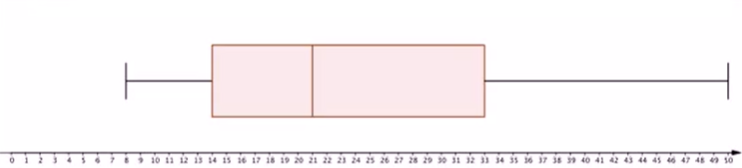
• 极差：
• 中位数：（说明有一半的树小于21岁，一半的树大于21岁）
• 树的四个年龄区间：
  • Q1（第一四分区间）：1/4的树在8~14岁之间。
  • Q2（第二四分区间）：1/4的树在14~21岁之间。
  • Q3（第三四分区间）：1/4的树在21~33岁之间。
  • Q4（第四四分区间）：1/4的树在33~50岁之间。
• 分析：虽然最老的树有50岁，但是中位数更接近于所有年龄的较低端。中位数作为集中趋势的测量标准，只有21岁，因此它离盒左侧及须左端较近，而离右边更远。