01. 统计学的基本认识
- 统计学是一门一切围绕数据进行的学科，大体上统计学可以分为描述统计学和推论统计学两类。
- 描述统计学：
- 假设有一大堆数据，向别人介绍所有数据是一件非常费时费力的事，因此希望在不介绍所有数据的情况下介绍这些数据的情况。
- 实现的方式是可以找到一些指示性的数字来代表所有的数据，而无需将所有的数据都介绍一次。
推论统计学：
01中有提到，对于要描述一组数组数据，描述性统计学的实现方式是找到一些指示性的数字来代表所有的数据，而无需将所有的数据都介绍一次。
- 这些最能代表一组数据的个别数字，这些数字被认为是能体现集中趋势（central tendency）的数字
集中趋势的三个指标：均值（mean）、中位数（median）、众数（mode）。
2.2 计算集中趋势
现有数据：1、3、2、1、4、1、4。
- 算术平均数（mean）：将所有数字相加，然后除以数字的数目。
- 中位数（median）：先将数据排好序，然后取中间的数字（若奇数个数据则直接取，若偶数个数据则取出中间两个求平均）。
-
2.3 为什么集中趋势有三个指标
总的来说，就是集中趋势中的每一个指标都无法在任何场景下完美的描述一组数据，必须要三个指标相互合作才可以。
- 如现有一组数据：3、3、3、3、3、100，它的三个集中趋势指标为：
- 可以发现，用
来描述这组数据的集中趋势明显不太合适，好像用中位数和众数来描述更加合适一点。 - 这是因为这组数据中存在一个特别大的值：100，而平均数这个指标就特别容易被这组特殊值（统计学中称之为异常值，或者离群值）所影响；相对而言中位数和众数在面对这种情况时就稳定得多。
因此，选择什么指标来准确的描述一组数据的集中趋势，是要根据具体情况进行具体分析的。
03. 样本和总体
3.1 总体和样本的概念
样本（sample）和总体（population）
- 总体与样本：总体即研究对象的整个群体，样本即从总体中随机选取的一部分。
- 样本数量和样本大小：样本数量即有多少个样本；样本大小又称样本容量，指的是每个样本里包含多少个数据。
- 示例：要想知道美国所有男性得平均身高。
- 总体：假设美国有3亿人口，男性占其中的50%，那么男性的总人数高达1.5亿人之多。
- 可行性：想要在同一时间实际测量美国每一位男性的身高这是几乎没可能做到的，而且哪怕就算测量做到了，计算1.5亿个值得三个集中趋势指标也是非常难做到的。
- 抽样统计：既然我们想知道总体的平均数是多少，那么最恰当的方法可能是从1.5亿人（总体）中随机抽取一些人（作为样本），取其平均值。
- 对于抽取样本而言随机是最重要的。因为如果样本中都是NCAA球员，或者都是侏儒，那其实这份样本并不能代表总体，因为这样测量出来的结果是与真实情况脱离的。
- 样本的数量越高，越可以代表总体；比如10个男性的样本平均数是1.81m，100w个男性的样本的平均数是1.7832m。那么1.7832m实际上更能代表美国男性的平均身高。
总结：要想了解一个较大的数据，而又懒得花功夫，那么采用抽样统计的方式无疑是最好的选择。
3.2 总体均值与样本均值
四个符号：
- N：表示总体数量；n：表示样本数量，即N中的任意一个子集（
）。 
：代表总体均值。
：代表样本均值。
- N：表示总体数量；n：表示样本数量，即N中的任意一个子集（
- 总体均值
：即所有数据的平均值，计算公式为：（N：总体数量；
：总体中的每一个数据）
- 样本均值
：即随机抽取的样本数据的平均值，计算公式为：（n：样本数量；
：样本中的每一个数据。）
这两个均值的计算方式实际上是一样的，只不过
的计算范围要比
来的大而已。
04. 离中趋势
4.1 集中趋势的缺陷与离中趋势的概念
平均数、中位数、众数都是用来衡量数据的集中趋势的。
- 有时候我们不知道集合中的数字是接近该集中趋势，还是远离该集中趋势，因此需要引入离中趋势来衡量。
- 如这里有两个数据集S1：2、2、3、3，S2：0、0、5、5。
- 计算两个数据集的总体均值：
、
。 - 发现两个总体的算术平均值相同，均为2.5。
- 但是这两个集合是不同的，S1中的所有数都接近2.5，而S2中的所有数相较于S1都远离2.5。
- 或者说S2相较于S1而言，其每个数字同均值的距离都较远；
- 也可以认为，均值虽然用来衡量集中趋势，但是不能很好地代表所有数字，如S2中的数字离均值的平均距离较远。
- 计算两个数据集的总体均值：
此时，可用于离中趋势（dispersion）来描述这组数据。
4.2 总体方差
离中趋势最经典的体现就是方差（variance），方差就是每点到均值距离的平方的平均值，直观来讲就是这些数据点离中间有多远。
- 方差又可分为总体方差和样本方差，这与
和
的关系类似。 - 总体方差记作：
，它求的是所有数据到总体均值距离的平方的平均值。
- 那么对于S1而言，要求它的
，可以先把每一项列出来。
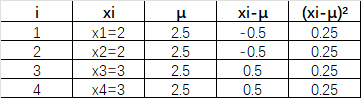
- 因此，S1的
为：
- 用同样的方法计算S2的
：
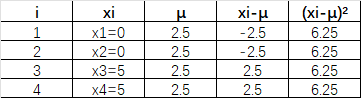
由此可以看出，虽然S1和S2的总体均值都是2.5，但是S1的总体方差为0.25，S2的总体方差为6.25。而方差越大，数据的离散程度越大，由此可以说S2中数据平均离均值比S1要远得多。
4.3 样本方差
总体方差和总体均值类似，在实际情况中一般都是得不到的，如以下两个场景：
- 要求全国男性的总体方差很难，因为这需要同时测量好几亿人的身高
- 总体完全不可能获得，如随机变量。
- 因此在很多时候，方差都只需要求样本方差，然后通过样本方差来估计总体方差。
样本方差计算公式：
标准差（Standard Deviation）是方差的平方根，即：
- 总体标准差：
- 样本标准差：
- 总体标准差：
- 示例1：现有一批数据：1、2、3、8、7，这些数据是总体时，求标准差。
（不推荐）
（推荐，该公式被称为总体方差的无偏估计）
- 示例2：还是数据：1、2、3、8、7，这些数据是样本时，求标准差。
4.5 诸方差公式
- 以总体方差为例，
可化简为：
（诸方差公式）。 - 化简过程：
- 传统的变量是可以变化，可以求解的量。如
中的
，确定一个自变量
，就可以得到一个应变量
。 - 随机变量（Random Variable）常用大写字母表示，如
。 与传统变量不同，随机变量虽然也可以取很多值，但是这些变量无法求解；因此随机变量实际上更像是一种函数，将随机过程映射到实际数值。
-
5.2.1 离散型随机变量
离散型随机变量（Discrete Type Random Variable）：其值域是一个有限区间，表示集合中的值是有限的，且可以一一列出，这样的随机变量称为离散型随机变量。
- 抛硬币不是1就是0这两种离散情况，故
是一个离散型随机变量。 - 投骰子是1到6的不同整数值，明天是否下雨也就下雨和不下雨两种情况；这些情况的结果都是可以一个个枚举出来的。
- 抛硬币不是1就是0这两种离散情况，故
- 离散型随机变量的概率分布也是离散化的：
- 如一颗正常的骰子投到每个数的概率都应该是
，因此它是均匀分布的：
- 如一颗正常的骰子投到每个数的概率都应该是
（若明天下雨，则随机变量
的值为1，否则为0）
（抛硬币得到的正反面是一个物理随机事件，随机变量
就用来量化这个随机实验）
- 硬币投掷的结果基本也是均匀分布的：
，则其概率为：- 可以看出，此时的分布就不是平均分布了。
- 根据图表可以进行一些计算，如求这颗骰子得到大于等于5的数字的概率。
所有离散点的概率和为1，这也同样适用于连续型随机变量，即随机变量的概率全部加起来必然为1。
5.2.2 连续型随机变量
连续型随机变量（Continuous Type Random Variable）：连续随机变量有无限个结果，可以取到无限集合中的任意一个值。
- 如明天雨量的英寸数：
。 - 明天的降雨量可能是1英寸，也可以是1.1英寸，也可能是1.111英寸、2.1111英寸、……，即描述这个可能值的有无穷个数字。
- 连续变量的另一种理解是其集合中任意两点间可以插入无穷多个点，如1到2之间可以插入1.1、1.2、1.32332、1.999999、……等无穷多个数点。
即其集合中的点是连续的，存在无穷无尽的可能数值，而不是离散化的。
5.3 连续型随机变量的概率密度函数
由于连续型随机变量的值的集合是连续的，因此其值对应的概率分布也是连续的。
- 因此对于连续型随机变量而言，其概率分布可以用概率密度函数表示。如加州明天的降雨量的概率密度函数可能是：
- 横轴表示明天的降雨量X，纵轴表示达到该降雨量的概率P。
- 现要求降雨量正好等于2英寸的概率，即
（错误说法）。- 根据之前对离散型随机变量的理解，
。 - 但是对于连续型随机变量而言，从逻辑上讲，
表示的是明天正好下2英寸雨的概率是多少。 - 即
代表的不是2.01英寸，也不是1.99英寸，不是1.99999英寸，也不是2.000001英寸。而是不多一个分子，也不少一个分子，正好2英寸。 - 在现实中，2.01、1.9998等都会被说成是2英寸，而降雨量正正好是2英寸的可能性极小（甚至现在人类的工具可能都无法测得降雨量正好是2英寸，不相差一点点）。因此，从实际情况出发，
并不现实，因为
并不接受除2之外的其他任何数据，哪怕是1.99999999。
- 根据之前对离散型随机变量的理解，
- 由此可得，对于连续型随机变量而言，要求正好某个值的概率，小数点后任意多位都不偏不倚，几乎是不可能的。
- 以降雨量为例，对于连续型随机变量而言，只能问
大概是2的概率是多少，故此时在2左右会允许一定容差，比如容差小于0.1，可以表示为：
或者
，即此时问的是
在1.9和2.1之间的概率。 - 从几何的角度出发，
的图像如下图所示。
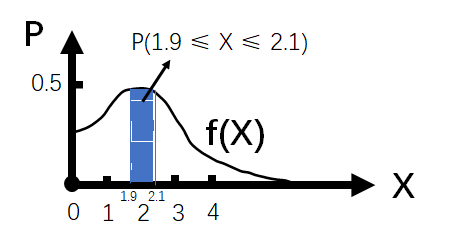
- 很明显，这块区域的面积可以用定积分表示，即：
- 并且根据概率的分布可得，
与
轴围成的面积恒等于1，即
。 - 其实从几何上也可以解释为什么连续型随机变量无法计算某一点的概率。以
为例，所得到的图像就是一条直线，而直线是没有面积的，故
。
若有收获，就点个赞吧
0 人点赞
