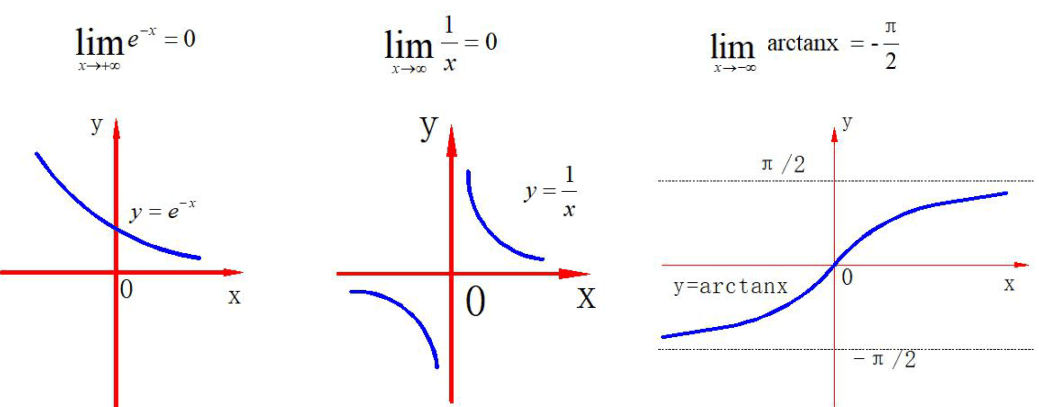01. 高等数学基础

01. 函数

1.1 函数的定义

• 函数通常用来描述量与量之间的关系，如描述的就是自变量与因变量之间的关系。
• 函数在处取得的函数值记作。

• 函数符号只是一种表示，也可以是：、、。

  1.2 几种函数特殊

• 分段函数：指当取不同值得时候，对应关系不同的一个函数。

• 反函数：
  • 即交换原函数自变量和因变量的对应关系，得到的新函数。
  • 如原函数的对应关系是。
  • 交换自变量和因变量的对应关系就变成了，展开即为。
• 显函数与隐函数：
  • 显函数：像这样直接表示对应关系的函数称为显函数，如。
  • 隐函数：这种不像显函数那样直接表明对应关系的函数称为隐函数，如。
  • 隐函数显化：即将隐函数从转化成的过程，如：

1.3 函数的几种特性

• 奇偶性：
  • 偶函数：函数图像关于轴对称，并且，如。
  • 奇函数：函数图像关于原点对称，并且，如、。

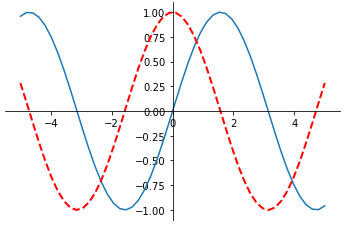
• 周期性：
  • 即函数的值有着这样的规律，其中被称为最小正周期。
  • 像、、为代表的这类函数值有周期变换规律的函数称为周期函数。

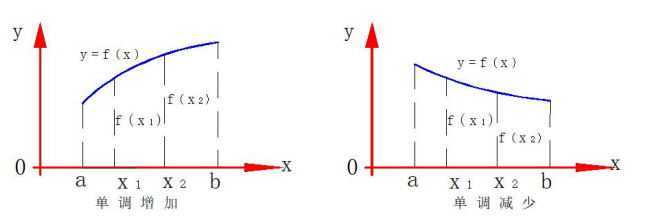
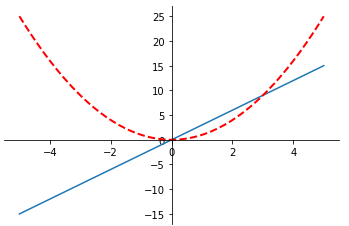
• 单调性：
  • 在取值区间上所有点的函数值都随自变量增大而增大，则称为单调递增。
  • 在取值区间上所有点的函数值都随自变量增大而增小，则称为单调递减。

02. 极限

2.1 极限的基本概念

2.1.1 数列

• 数列即按照一定次序排列的一列数，如：，其中称作这个数列的通项。
• 对于数列：
  • 如果当无限增大时，其通向无限接近于一个常数，则称该数列以为极限，或称数列收敛于，并认为此时极限存在并等于。

• 如：、。
• 否则称数列为发散，并认为此时极限不存在。如：（极限不存在，即数列发散）。

  2.1.2 极限的符号表示

• 表示当无限增大时，即当无限向增大，并向无限减少的两种情况时。。
• 表示当无限增大时。
• 表示当无限减少时。
• 表示当从的左右两侧无限接近于时。
• 表示当从的右侧无限接近于时。

• 表示当从的左侧无限接近于时。

  2.1.3 几个常见的函数极限

  

  2.1.4 函数极限存在法则

• 函数在的去心邻域内有定义，即。

• 左右极限相等：可得出。
  • 左极限：
  • 右极限：

• 示例：现有一个分段函数，判断当时，的极限是否存在。

  • 解：

    2.2 无穷大与无穷小

    2.2.1 无穷小

• 无穷小指的是以零为极限，如：

  • ，则称是时的无穷小。
  • ，则称是时的无穷小。
• 无穷小的基本性质：
  • 有限个无穷小的和与积仍然是无穷小。
  • 有界变量与无穷小的乘积仍是无穷小。

• 无限个无穷小之和不一定是无穷小。

• 无穷小的商不一定是无穷小。

• 极限与无穷小的关系：的充要条件为，其中是时的无穷小。

  2.2.2 无穷大

• 无穷大的定义：

  • 无穷大并不是一个很大的数，无穷大是相对于变化过程来说的。

或

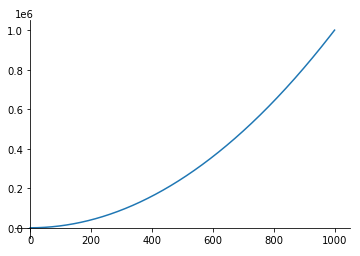
• 像来说，其值是无限增大的，没有一个收敛的点

• 无穷大和无穷小的关系：在自变量的同一变化过程中，若为无穷大，那么为无穷小。

  2.2.3 无穷小的比较

• 当时，都是无穷小，即：

• 如果：

  • ，则称是比高阶的无穷小。
  • ，则称是比低价的无穷小。
  • ，则称是的同阶无穷小。
  • ，则称是的等价无穷小，记作。

    03. 函数的连续性

    3.1 连续

    3.1.1 函数连续的定义

• 设函数在点的某邻域内有定义，如果当自变量的该变量趋近于零时，相应函数的改变量也趋近于零，则称在点处连续。

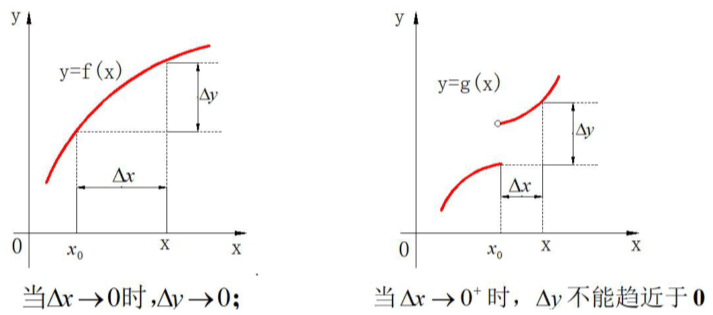
• 即：
• 几何表示：（左图连续；右图间断）

3.1.2 函数连续的条件

• 函数在点处连续，需要满足三个条件：
  • 函数在该点处有定义。
  • 函数在该点处极限值存在。
  • 极限值等于函数值。
• 示例：求函数在处的连续性。

3.2 间断

3.2.1 间断点的定义

• 函数在点处不连续，则称为函数的间断点。

• 满足以下三种情况之一的，即为间断点：

  • 函数在点处没有定义，如函数在处无定义。
  • 极限不存在。
  • 点处函数的极限值不等于函数值，即

    3.2.2 间断点的分类

• 当时，的左右极限存在，则称为的第一类间断点，否则为第二类间断点。

• 第一类间断点又可细分为可去间断点和跳跃间断点：
  • 可去间断点：存在但不等于。
  • 跳跃间断点：与均存在，但不相等。

• 示例：判断函数的连续性。

  • ，所以函数在处无定义。
  • ，所以是的可去间断点。
  • ，所以是的第二类间断点。

    04. 导数

    4.1 导数的基本认识

    4.1.1 导数的定义

• 现有平均速度公式，其中s表示路程，t表示时间。求瞬时速度。

  • 瞬时速度 = 瞬时经过的路程 / 瞬时时间。（瞬时实际即时间变化无限接近于0的一个时间，即）
  • 瞬时经过的路程：
  • 这一小段的平均速度：
  • 那么时刻的瞬时速度实际上就是当的速度，即：

• 如果平均变化率的极限存在，
• 则称此极限为函数在点处的导数，记作，或者：

4.1.2 常见函数的导数

• 常数函数与幂函数：、
• 三角函数与反三角函数：
  • 、、
  • 、、
    • 补充：、、。
  • 、、、

• 指数函数与对数函数：

  • 、
  • 、

    4.1.3 求导公式

• 

• 
• 
• 

• 【推导式：】

  4.2 偏导数

  4.2.1 一元&二元函数变化关系

• 对于一元函数只存在随的变化。

• 但是对于一个二元函数，却存在三种关系：
  • 随变化的变化率；
  • 随变化的变化率；
  • 随同时变化的变化率。

4.2.2 偏导数的定义

• 设函数在点的某个邻域内有定义。
• 令，即固定的值，此时实际上可以看成一个一元函数，因为固定不变。
  • 如；
  • 当时，。
• 此时一元函数在点处可导，由此得到极限：

• 则称为函数在点处关于自变量的偏导数，记作，或者：

• 补充：上述过程是固定，然后对求偏导；同样的，也可以固定，然后对求偏导。

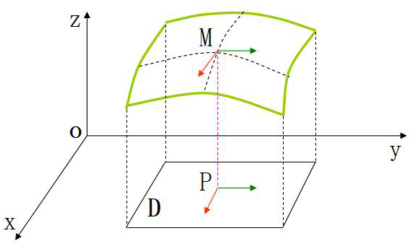
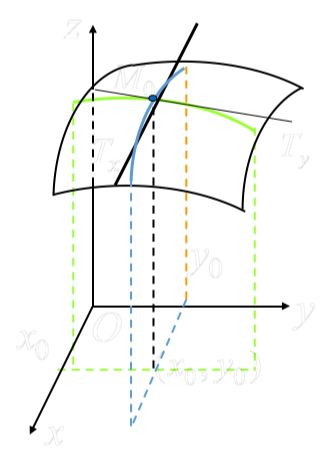
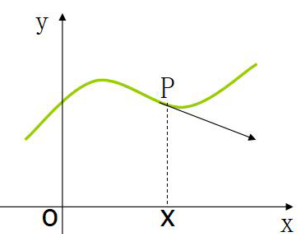
  4.2.3 偏导数的几何意义

• 在空间直角坐标系中存在一个曲面，（投影平行于轴）和（投影平行于轴）是这个曲面过点的两条切线。

• 那么：
  • 是曲线在点处的切线对轴的斜率。
  • 是曲线在点处的切线对轴的斜率。

4.2.4 求偏导练习

• 求在点处的偏导数。
  • 固定（即把当作一个常数），对求偏导。

• 固定（即把当作一个常数），对求偏导。

• 待入点，得到偏导数。

4.3 方向导数

4.3.1 方向导数的意义

• 方向导数是梯度的基础，而梯度下降等概念在ML中尤为重要。
• 在ML中，对于一个问题很少会有直接可求解的情况，大多数时候解决问题的思想都是去优化模型，那么朝着怎样的一个方向优化，才能让模型越来越好，就需要用到梯度和方向导数相关的知识。
• 从几何上理解方向导数：现在有一点处着火了，而这一点处有一只蚂蚁，问蚂蚁沿着什么方向跑才能存活？这种问题就可以用方向导数求解。

4.3.2 方向导数

• 关于下图存在一个函数，和一个方向（这个方向由点和点确定），可得：
  • 两点之间的距离：
  • 两点之间关于的增量：

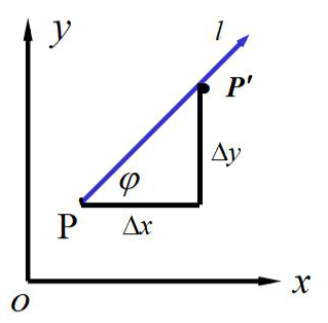
• 如果函数的增量与这两点的距离的比例存在，则在点沿着的方向导数为：

• 单位向量的方向导数：

  • 函数在轴正方向单位向量，轴正方向单位向量的方向导数分别为；
  • 负方向导数分别为。

    4.3.3 方向导数的定理

• 补充知识：

  • 函数可微分的必要条件：
    • 对于一元函数而言，可微等价于可导；由于函数可导一定，连续不一定可导，因此若一元函数在某点处可微分，则函数在该点必连续。
    • 若二元函数在某点可微分，则该函数在该点对和的偏导数必存在。
  • 充分条件：若函数对和的偏导数在这点的某一领域内都存在，且均在这点连续，则该函数在这点可微。
• 方向导数的定理：如果函数在点是可微分的，那么在该点沿任意方向的方向导数都存在，且为：

（为轴与方向的夹角）

4.3.4 方向导数应用

• 求函数在点处沿从点到的方向的方向导数。
  • 求：

• 求偏导：

• 求方向导数：

4.4 梯度1