结论先行

节选 https://www.jianshu.com/p/4e2b20333d38

作用

降维后再求相似度，减少计算量。
对于没有评价过商品的用户，所有商品的推荐结果都是0。

数据集中行代表用户user，列代表物品item，其中的值代表用户对物品的打分。基于SVD的优势在于：用户的评分数据是稀疏矩阵，可以用SVD将原始数据映射到低维空间中，然后计算物品item之间的相似度，可以节省计算资源。

整体思路

先找到用户没有评分的物品，然后再经过SVD“压缩”后的低维空间中，计算未评分物品与其他物品的相似性，得到一个预测打分，再对这些物品的评分从高到低进行排序，返回前N个物品推荐给用户。
具体代码如下，主要分为5部分：

  • 第1部分：加载测试数据集；
  • 第2部分：定义三种计算相似度的方法；
  • 第3部分：通过计算奇异值平方和的百分比来确定将数据降到多少维才合适，返回需要降到的维度；
  • 第4部分：在已经降维的数据中，基于SVD对用户未打分的物品进行评分预测，返回未打分物品的预测评分值；
  • 第5部分：产生前N个评分值高的物品，返回物品编号以及预测评分值。

优势

用户的评分数据是稀疏矩阵，可以用SVD将数据映射到低维空间，然后计算低维空间中的item之间的相似度，对用户未评分的item进行评分预测，最后将预测评分高的item推荐给用户。

参考代码

验证过，可以直接跑通。建议理解了SVD算法后来执行。可以打印中间过程看看情况。

  1. # coding=utf-8
  2. from numpy import *
  3. from numpy import linalg as la
  5. '''加载测试数据集'''
  8. def loadExData():
  9.     return mat([[0, 0, 0, 0, 0, 4, 0, 0, 0, 0, 5],
  10.                 [0, 0, 0, 3, 0, 4, 0, 0, 0, 0, 3],
  11.                 [0, 0, 0, 0, 4, 0, 0, 1, 0, 4, 0],
  12.                 [3, 3, 4, 0, 0, 0, 0, 2, 2, 0, 0],
  13.                 [5, 4, 5, 0, 0, 0, 0, 5, 5, 0, 0],
  14.                 [0, 0, 0, 0, 5, 0, 1, 0, 0, 5, 0],
  15.                 [4, 3, 4, 0, 0, 0, 0, 5, 5, 0, 1],
  16.                 [0, 0, 0, 4, 0, 4, 0, 0, 0, 0, 4],
  17.                 [0, 0, 0, 2, 0, 2, 5, 0, 0, 1, 2],
  18.                 [0, 0, 0, 0, 5, 0, 0, 0, 0, 4, 0],
  19.                 [1, 0, 0, 0, 0, 0, 0, 1, 2, 0, 0]])
  22. '''以下是三种计算相似度的算法，分别是欧式距离、皮尔逊相关系数和余弦相似度,
  23. 注意三种计算方式的参数inA和inB都是列向量'''
  24. #这段代码在机器学习实战书中P259
  25. #（注意传入的inA,inB都是列向量，行向量会报错）
  27. def ecludSim(inA, inB):
  28.     return 1.0 / (1.0 + la.norm(inA - inB))  # 范数的计算方法linalg.norm()，这里的1/(1+距离)表示将相似度的范围放在0与1之间
  31. def pearsSim(inA, inB):
  32.     if len(inA) < 3: return 1.0
  33.     return 0.5 + 0.5 * corrcoef(inA, inB, rowvar=0)[0][
  34.         1]  # 皮尔逊相关系数的计算方法corrcoef()，参数rowvar=0表示对列求相似度，这里的0.5+0.5*corrcoef()是为了将范围归一化放到0和1之间
  37. def cosSim(inA, inB):
  38.     num = float(inA.T * inB)
  39.     denom = la.norm(inA) * la.norm(inB)
  40.     return 0.5 + 0.5 * (num / denom)  # 将相似度归一到0与1之间
  43. '''按照前k个奇异值的平方和占总奇异值的平方和的百分比percentage来确定k的值,
  44. 后续计算SVD时需要将原始矩阵转换到k维空间'''
  47. def sigmaPct(sigma, percentage):
  48.     sigma2 = sigma ** 2  # 对sigma求平方
  49.     sumsgm2 = sum(sigma2)  # 求所有奇异值sigma的平方和
  50.     sumsgm3 = 0  # sumsgm3是前k个奇异值的平方和
  51.     k = 0
  52.     for i in sigma:
  53.         sumsgm3 += i ** 2
  54.         k += 1
  55.         if sumsgm3 >= sumsgm2 * percentage:
  56.             return k
  59. '''函数svdEst()的参数包含：数据矩阵、用户编号、物品编号和奇异值占比的阈值，
  60. 数据矩阵的行对应用户，列对应物品，函数的作用是基于item的相似性对用户未评过分的物品进行预测评分'''
  63. def svdEst(dataMat, user, simMeas, item, percentage):
  64.     n = shape(dataMat)[1]
  65.     simTotal = 0.0;
  66.     ratSimTotal = 0.0
  67.     u, sigma, vt = la.svd(dataMat)
  68.     k = sigmaPct(sigma, percentage)  # 确定了k的值
  69.     sigmaK = mat(eye(k) * sigma[:k])  # 构建对角矩阵
  70.     xformedItems = dataMat.T * u[:, :k] * sigmaK.I  # 根据k的值将原始数据转换到k维空间(低维),xformedItems表示物品(item)在k维空间转换后的值
  71.     for j in range(n):
  72.         userRating = dataMat[user, j]
  73.         if userRating == 0 or j == item: continue
  74.         similarity = simMeas(xformedItems[item, :].T, xformedItems[j, :].T)  # 计算物品item与物品j之间的相似度
  75.         simTotal += similarity  # 对所有相似度求和
  76.         ratSimTotal += similarity * userRating  # 用"物品item和物品j的相似度"乘以"用户对物品j的评分"，并求和
  77.     if simTotal == 0:
  78.         return 0
  79.     else:
  80.         return ratSimTotal / simTotal  # 得到对物品item的预测评分
  83. '''函数recommend()产生预测评分最高的N个推荐结果，默认返回5个；
  84. 参数包括：数据矩阵、用户编号、相似度衡量的方法、预测评分的方法、以及奇异值占比的阈值；
  85. 数据矩阵的行对应用户，列对应物品，函数的作用是基于item的相似性对用户未评过分的物品进行预测评分；
  86. 相似度衡量的方法默认用余弦相似度
  87. '''
  90. def recommend(dataMat, user, N=5, simMeas=cosSim, estMethod=svdEst, percentage=0.9):
  91.     unratedItems = nonzero(dataMat[user, :].A == 0)[1]  # 建立一个用户未评分item的列表
  92.     if len(unratedItems) == 0: return 'you rated everything'  # 如果都已经评过分，则退出
  93.     itemScores = []
  94.     for item in unratedItems:  # 对于每个未评分的item，都计算其预测评分
  95.         estimatedScore = estMethod(dataMat, user, simMeas, item, percentage)
  96.         itemScores.append((item, estimatedScore))
  97.     itemScores = sorted(itemScores, key=lambda x: x[1], reverse=True)  # 按照item的得分进行从大到小排序
  99.     return itemScores[:N]  # 返回前N大评分值的item名，及其预测评分值
  101. #下面来调用一下：
  102. testdata = loadExData()
  103. top = recommend(testdata, 1, N=3, percentage=0.8) # 对编号为1的用户推荐评分较高的3件商品
  104. for Top in top :
  105.     item , estimatedScore = Top
  106.     print(item  , estimatedScore)

SVD算法理论

拷贝：https://blog.csdn.net/shenziheng1/article/details/52916278

1.前言

第一次接触奇异值分解还是在本科期间，那个时候要用到点对点的刚体配准，这是查文献刚好找到了四元数理论用于配准方法（点对点配准可以利用四元数方法，如果点数不一致更建议应用ICP算法）。一直想找个时间把奇异值分解理清楚、弄明白，直到今天才系统地来进行总结。
上一次学习过关于PCA的文章，PCA的实现一般有两种，一种是用特征值分解去实现的，一种是用奇异值分解去实现的。特征值和奇异值在大部分人的印象中，往往是停留在纯粹的数学计算中。而且线性代数或者矩阵论里面，也很少讲任何跟特征值与奇异值有关的应用背景。奇异值分解是一个有着很明显的物理意义的一种方法，它可以将一个比较复杂的矩阵用更小更简单的几个子矩阵的相乘来表示，这些小矩阵描述的是矩阵的重要的特性。就像是描述一个人一样，给别人描述说这个人长得浓眉大眼，方脸，络腮胡，而且带个黑框的眼镜，这样寥寥的几个特征，就让别人脑海里面就有一个较为清楚的认识，实际上，人脸上的特征是有着无数种的，之所以能这么描述，是因为人天生就有着非常好的抽取重要特征的能力，让机器学会抽取重要的特征，SVD是也一个重要的方法。在机器学习领域，有相当多的应用与奇异值都可以扯上关系，比如做feature reduction的PCA，做数据压缩（以图像压缩为代表）的算法，还有做搜索引擎语义层次检索的LSI（Latent Semantic Indexing）。
本文主要关注奇异值的一些特性，还会稍稍提及奇异值的计算。另外，本文里面有部分不算太深的线性代数的知识，如果完全忘记了线性代数，看文可能会有些困难。

2.奇异值分解详解

特征值分解和奇异值分解两者有着很紧密的关系，特征值分解和奇异值分解的目的都是一样，就是提取出一个矩阵最重要的特征。先谈谈特征值分解吧：

2.1 特征值

如果说一个向量v是方阵A的特征向量，将一定可以表示成下面的形式：
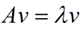
image.png
这时候λ就被称为特征向量v对应的特征值，一个矩阵的一组特征向量是一组正交向量。特征值分解是将一个矩阵分解成下面的形式：
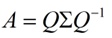
image.png
其中Q是这个矩阵A的特征向量组成的矩阵，Σ是一个对角阵，每一个对角线上的元素就是一个特征值。首先，要明确的是，一个矩阵其实就是一个线性变换，因为一个矩阵乘以一个向量后得到的向量，其实就相当于将这个向量进行了线性变换。比如说下面的一个矩阵：
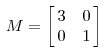
image.png
它其实对应的线性变换是下面的形式：
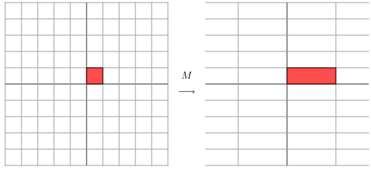
image.png
因为这个矩阵M乘以一个向量(x,y)的结果是：
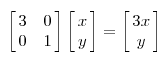
image.png
上面的矩阵是对称的，所以这个变换是一个对x，y轴的方向一个拉伸变换（每一个对角线上的元素将会对一个维度进行拉伸变换，当值>1时拉长，当值<1时缩短），当矩阵不是对称的时候，假如说矩阵是下面的样子：
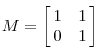
image.png
它所描述的变换是下面的样子：
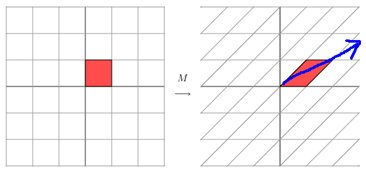
image.png
这其实是在平面上对一个轴进行的拉伸变换（如蓝色的箭头所示），在图中，蓝色的箭头是一个最主要的变化方向（变化方向可能有不止一个），如果我们想要描述好一个变换，那我们就描述好这个变换主要的变化方向就好了。反过头来看看之前特征值分解的式子，分解得到的Σ矩阵是一个对角阵，里面的特征值是由大到小排列的，这些特征值所对应的特征向量就是描述这个矩阵变化方向（从主要的变化到次要的变化排列）
当矩阵是高维的情况下，那么这个矩阵就是高维空间下的一个线性变换，这个线性变化可能没法通过图片来表示，但是可以想象，这个变换也同样有很多的变换方向，我们通过特征值分解得到的前N个特征向量，那么就对应了这个矩阵最主要的N个变化方向。我们利用这前N个变化方向，就可以近似这个矩阵（变换）。也就是之前说的：提取这个矩阵最重要的特征。总结一下，特征值分解可以得到特征值与特征向量，特征值表示的是这个特征到底有多重要，而特征向量表示这个特征是什么，可以将每一个特征向量理解为一个线性的子空间，我们可以利用这些线性的子空间干很多的事情。不过，特征值分解也有很多的局限，比如说变换的矩阵必须是方阵。

2.2 奇异值

下面重点谈谈奇异值分解。特征值分解是一个提取矩阵特征很不错的方法，但是它只是对方阵而言的，在现实的世界中，我们看到的大部分矩阵都不是方阵，比如说有N个学生，每个学生有M科成绩，这样形成的一个N M的矩阵就不可能是方阵，我们怎样才能描述这样普通的矩阵呢的重要特征呢？奇异值分解可以用来干这个事情，奇异值分解是一个能适用于任意的矩阵的一种分解的方法：
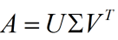
image.png
假设A是一个N M的矩阵，那么得到的U是一个N N的方阵（里面的向量是正交的，U里面的向量称为左奇异向量），Σ是一个N M的矩阵（除了对角线的元素都是0，对角线上的元素称为奇异值），V’(V的转置)是一个N N的矩阵，里面的向量也是正交的，V里面的向量称为右奇异向量），如下图所示：
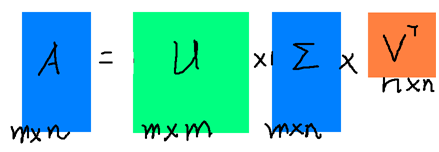
image.png
那么奇异值和特征值是怎么对应起来的呢？首先，我们将一个矩阵A的转置 A，将会得到一个方阵，我们用这个方阵求特征值可以得到：
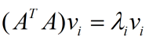
image.png
这里得到的v，就是我们上面的右奇异向量。此外我们还可以得到：
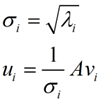
image.png
这里的σ就是上面说的奇异值，u就是上面说的左奇异向量。奇异值σ跟特征值类似，在矩阵Σ中也是从大到小排列，而且σ的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了。也就是说，我们也可以用前r大的奇异值来近似描述矩阵，这里定义一下部分奇异值分解：
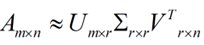
image.png
r是一个远小于m、n的数，这样矩阵的乘法看起来像是下面的样子：
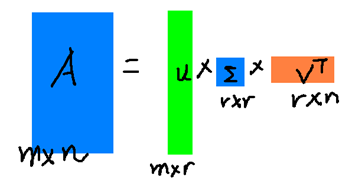
image.png

SVD算法的物理意义

节选:https://zhuanlan.zhihu.com/p/25801478
SVD全称Singular value decomposition，奇异值分解。线性代数里重要的一种分解形式，其矩阵的特殊含义可以用来做处理线性相关。如在自然语言处理中，对新闻的分类，就可以采用SVD的方法，而且已取得不错的效果。把新闻中的核心词，用一个向量进行表示，每条新闻一个向量，组成一个矩阵，对矩阵进行SVD分解。如：可以用一个大矩阵A来描述这一百万篇文章和五十万词的关联性。这个矩阵中，每一行对应一篇文章，每一列对应一个词。
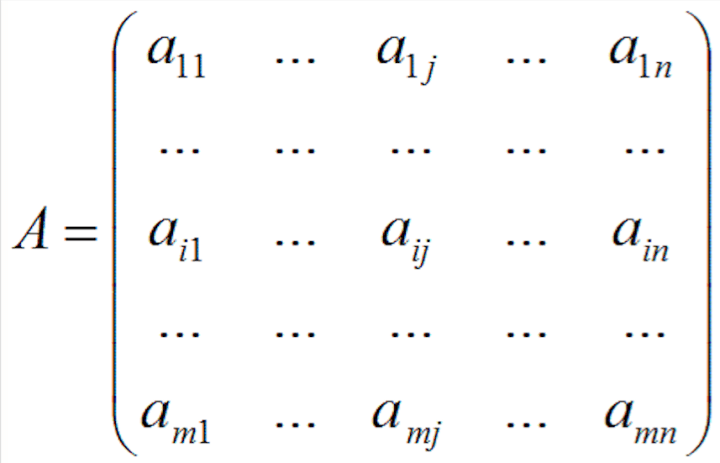
image.png
在上面的图中，M=1,000,000，N=500,000。第 i 行，第 j 列的元素，是字典中第 j 个词在第 i 篇文章中出现的加权词频（比如，TF/IDF)。读者可能已经注意到了，这个矩阵非常大，有一百万乘以五十万，即五千亿个元素。
奇异值分解就是把上面这样一个大矩阵，分解成三个小矩阵相乘，如下图所示。比如把上面的例子中的矩阵分解成一个一百万乘以一百的矩阵X，一个一百乘以一百的矩阵B，和一个一百乘以五十万的矩阵Y。这三个矩阵的元素总数加起来也不过1.5亿，仅仅是原来的三千分之一。相应的存储量和计算量都会小三个数量级以上。
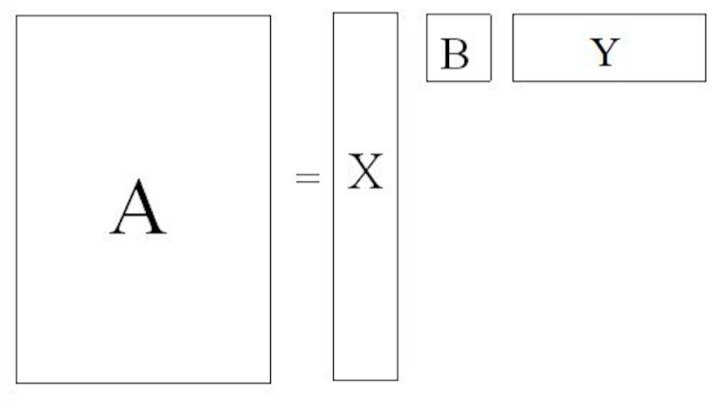
image.png
三个矩阵有非常清楚的物理含义：

  • 第一个矩阵X中的每一行表示意思相关的一类词，其中的每个非零元素表示这类词中每个词的重要性（或者说相关性），数值越大越相关。
  • 第三个矩阵Y中的每一列表示同一主题一类文章，其中每个元素表示这类文章中每篇文章的相关性。
  • 第二个矩阵B则表示类词和文章之间的相关性。因此，我们只要对关联矩阵A进行一次奇异值分解，我们就可以同时完成了近义词分类和文章的分类。（同时得到每类文章和每类词的相关性）。

例子

有如下数据表，虽然行列转置了，但不影响我们的结果。

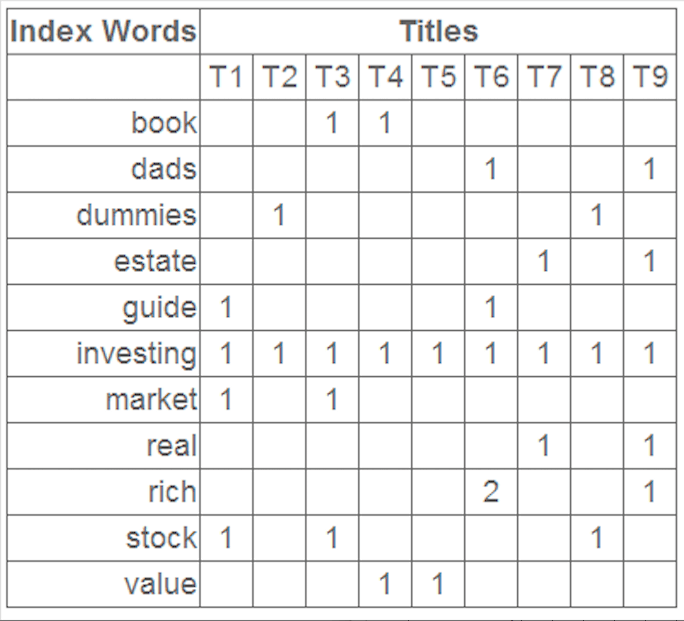
image.png
这就是一个矩阵，不过不太一样的是，这里的一行表示一个词在哪些title中出现了（一行就是之前说的一维feature），一列表示一个title中有哪些词，（这个矩阵其实是我们之前说的那种一行是一个sample的形式的一种转置，这个会使得我们的左右奇异向量的意义产生变化，但是不会影响我们计算的过程）。比如说T1这个title中就有guide、investing、market、stock四个词，各出现了一次，我们将这个矩阵进行SVD，得到下面的矩阵：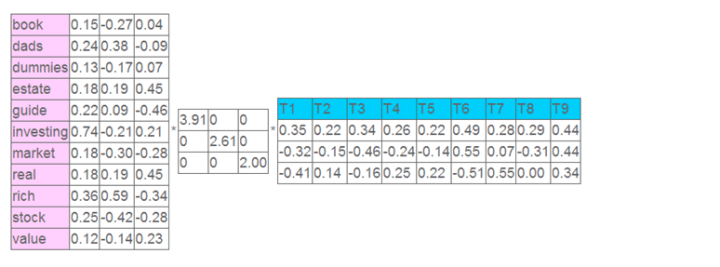
image.png
左奇异向量表示词的一些特性，右奇异向量表示文档的一些特性，中间的奇异值矩阵表示左奇异向量的一行与右奇异向量的一列的重要程序，数字越大越重要。
继续看这个矩阵还可以发现一些有意思的东西，首先，左奇异向量的第一列表示每一个词的出现频繁程度，虽然不是线性的，但是可以认为是一个大概的描述，比如book是0.15对应文档中出现的2次，investing是0.74对应了文档中出现了9次，rich是0.36对应文档中出现了3次；
其次，右奇异向量中一的第一行表示每一篇文档中的出现词的个数的近似，比如说，T6是0.49，出现了5个词，T2是0.22，出现了2个词。

然后我们反过头来看，我们可以将左奇异向量和右奇异向量都取后2维（之前是3维的矩阵），投影到一个平面上，可以得到：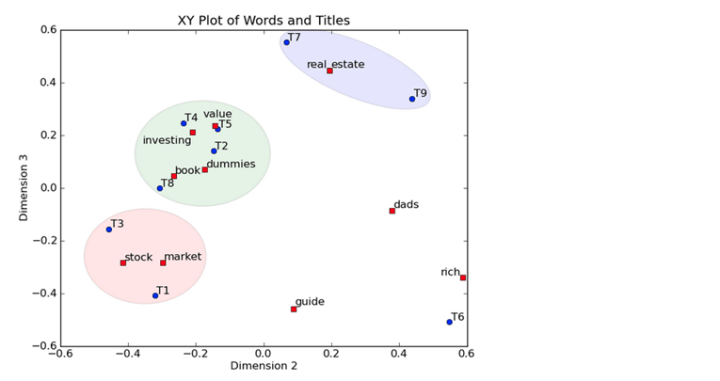
image.png
在图上，每一个红色的点，都表示一个词，每一个蓝色的点，都表示一篇文档，这样我们可以对这些词和文档进行聚类，比如说stock 和 market可以放在一类，因为他们老是出现在一起，real和estate可以放在一类，dads，guide这种词就看起来有点孤立了，我们就不对他们进行合并了。按这样聚类出现的效果，可以提取文档集合中的近义词，这样当用户检索文档的时候，是用语义级别（近义词集合）去检索了，而不是之前的词的级别。这样一减少我们的检索、存储量，因为这样压缩的文档集合和PCA是异曲同工的，二可以提高我们的用户体验，用户输入一个词，我们可以在这个词的近义词的集合中去找，这是传统的索引无法做到的。