原文链接：https://blog.csdn.net/zengxiantao1994/java/article/details/72787849
以前多次接触过极大似然估计，但一直都不太明白到底什么原理，最近在看贝叶斯分类，对极大似然估计有了新的认识，总结如下：
贝叶斯决策
首先来看贝叶斯分类，我们都知道经典的贝叶斯公式：<br /> <br /> 其中：<br />：为先验概率，表示每种类别分布的概率；<br />：类条件概率，表示在某种类别前提下，某事发生的概率；<br /> :为后验概率，表示某事发生了，并且它属于某一类别的概率，有了这个后验概率，我们就可以对样本进行分类。后验概率越大，说明某事物属于这个类别的可能性越大，我们越有理由把它归到这个类别下。
例子
我们来看一个直观的例子：**已知**：在夏季，某公园男性穿凉鞋的概率为1/2，女性穿凉鞋的概率为2/3，并且该公园中男女比例通常为2:1。**问题**：若你在公园中随机遇到一个穿凉鞋的人，请问他的性别为男性或女性的概率分别为多少？<br /> 从问题看，就是上面讲的，某事发生了，它属于某一类别的概率是多少？即后验概率。设： <br /> 由已知可得：<br /><br /> 男性和女性穿凉鞋相互独立，所以<br /> <br />（若只考虑分类问题，只需要比较后验概率的大小，的取值并不重要）。<br /> 由贝叶斯公式算出：<br />
问题引出
但是在实际问题中并不都是这样幸运的，我们能获得的数据可能只有有限数目的样本数据，而先验概率和类条件概率(各类的总体分布)都是未知的。根据仅有的样本数据进行分类时，一种可行的办法是我们需要先对先验概率和类条件概率进行估计，然后再套用贝叶斯分类器。先验概率的估计较简单，1、每个样本所属的自然状态都是已知的（有监督学习）；2、依靠经验；3、用训练样本中各类出现的频率估计。类条件概率的估计（非常难），原因包括：概率密度函数包含了一个随机变量的全部信息；样本数据可能不多；特征向量x的维度可能很大等等。总之要直接估计类条件概率的密度函数很难。解决的办法就是，把估计完全未知的概率密度转化为估计参数。这里就将概率密度估计问题转化为参数估计问题，极大似然估计就是一种参数估计方法。当然了，概率密度函数的选取很重要，模型正确，在样本区域无穷时，我们会得到较准确的估计值，如果模型都错了，那估计半天的参数，肯定也没啥意义了。
重要前提
上面说到，参数估计问题只是实际问题求解过程中的一种简化方法（由于直接估计类条件概率密度函数很困难）。所以能够使用极大似然估计方法的样本必须需要满足一些前提假设。重要前提：训练样本的分布能代表样本的真实分布。每个样本集中的样本都是所谓独立同分布的随机变量 (iid条件)，且有充分的训练样本。
极大似然估计
极大似然估计的原理，用一张图片来说明，如下图所示：
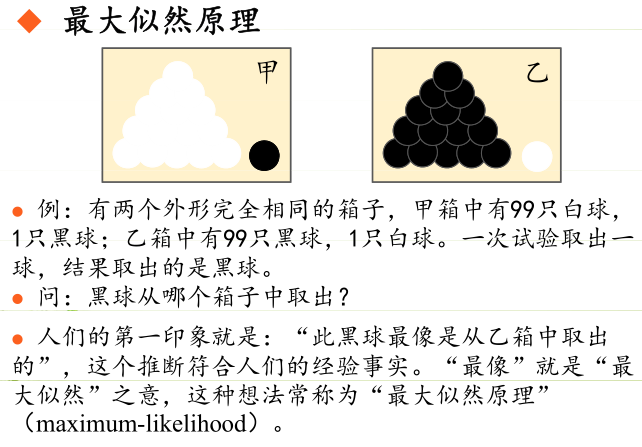
总结起来，最大似然估计的目的就是：利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。原理：极大似然估计是建立在极大似然原理的基础上的一个统计方法，是概率论在统计学中的应用。极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。通过若干次试验，观察其结果，利用试验结果得到某个参数值能够使样本出现的概率为最大，则称为极大似然估计。由于样本集中的样本都是独立同分布，可以只考虑一类样本集D，来估计参数向量θ。记已知的样本集为：<br />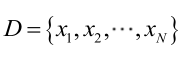<br /> 似然函数（linkehood function）：联合概率密度函数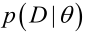称为相对于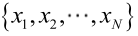的θ的似然函数。<br />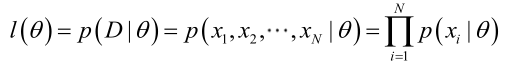<br /> 如果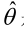是参数空间中能使似然函数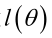最大的θ值，则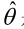应该是“最可能”的参数值，那么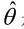就是θ的极大似然估计量。它是样本集的函数，记作：<br />
求解极大似然函数
ML估计：求使得出现该组样本的概率最大的θ值。<br />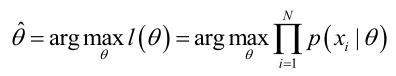<br /> 实际中为了便于分析，定义了对数似然函数：<br />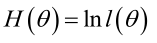<br />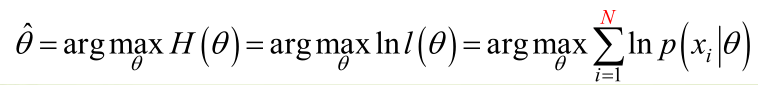<br /> 1. 未知参数只有一个（θ为标量）在似然函数满足连续、可微的正则条件下，极大似然估计量是下面微分方程的解：
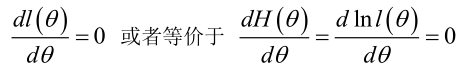
2.未知参数有多个（θ为向量）则θ可表示为具有S个分量的未知向量：<br />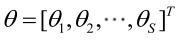<br /> 记梯度算子：<br />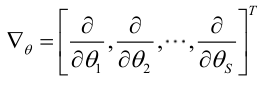若似然函数满足连续可导的条件，则最大似然估计量就是如下方程的解。<br />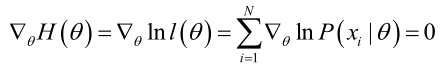方程的解只是一个估计值，只有在样本数趋于无限多的时候，它才会接近于真实值。
极大似然估计的例子
例1：设样本服从正态分布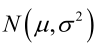，则似然函数为：<br />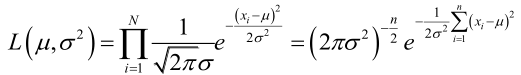它的对数：<br />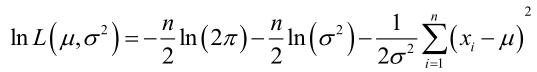<br /> 求导，得方程组：<br />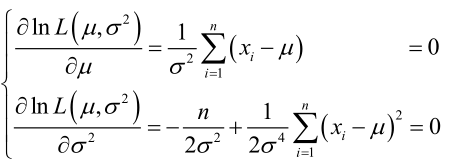<br /> 联合解得：<br />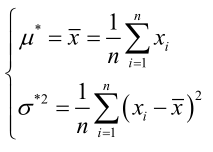似然方程有唯一解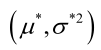：，而且它一定是最大值点，这是因为当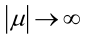或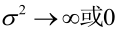时，非负函数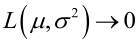。于是U和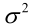的极大似然估计为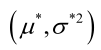。例2：设样本服从均匀分布[a, b]。则X的概率密度函数：<br />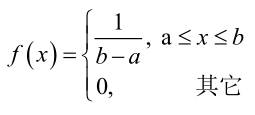<br /> 对样本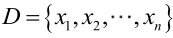：<br />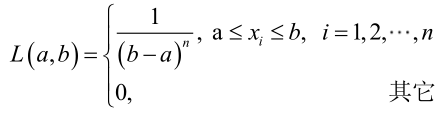很显然，L(a,b)作为a和b的二元函数是不连续的，这时不能用导数来求解。而必须从极大似然估计的定义出发，求L(a,b)的最大值，为使L(a,b)达到最大，b-a应该尽可能地小，但b又不能小于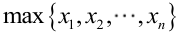，否则，L(a,b)=0。类似地a不能大过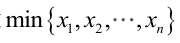，因此，a和b的极大似然估计：<br />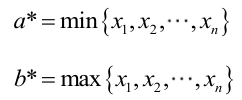
总结
求最大似然估计量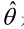
的一般步骤：
（1）写出似然函数；（2）对似然函数取对数，并整理；（3）求导数；（4）解似然方程。最大似然估计的特点：1.比其他估计方法更加简单；2.收敛性：无偏或者渐近无偏，当样本数目增加时，收敛性质会更好；3.如果假设的类条件概率模型正确，则通常能获得较好的结果。但如果假设模型出现偏差，将导致非常差的估计结果。
若有收获，就点个赞吧
0 人点赞
