千言万语最终汇成的一幅图：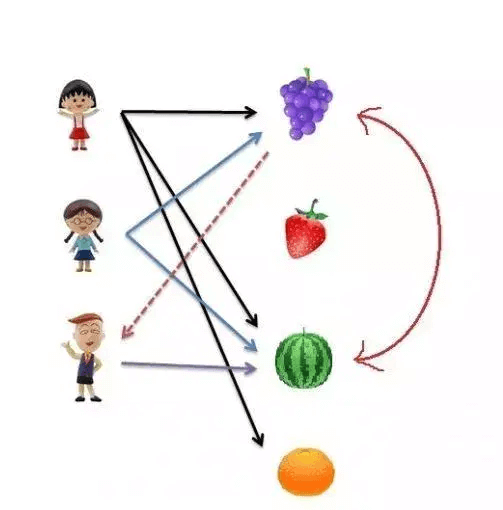
image.png
以用户为基础的协同推荐算法随着用户数量的增多，计算的时间就会变长，所以在2001年Sarwar提出了基于项目的协同过滤推荐算法(Item-based Collaborative Filtering Algorithms)。以项目为基础的协同过滤方法有一个基本的假设“能够引起用户兴趣的项目，必定与其之前评分高的项目相似”，通过计算项目之间的相似性来代替用户之间的相似性。

2.1 步骤

1.收集用户信息
同以用户为基础（User-based）的协同过滤。
2.针对项目的最近邻搜索
先计算已评价项目和待预测项目的相似度，并以相似度作为权重，加权各已评价项目的分数，得到待预测项目的预测值。例如：要对项目 A 和项目 B 进行相似性计算，要先找出同时对 A 和 B 打过分的组合，对这些组合进行相似度计算，常用的算法同以用户为基础（User-based）的协同过滤。
3.产生推荐结果
以项目为基础的协同过滤不用考虑用户间的差别，所以精度比较差。但是却不需要用户的历史数据，或是进行用户识别。对于项目来讲，它们之间的相似性要稳定很多，因此可以离线完成工作量最大的相似性计算步骤，从而降低了在线计算量，提高推荐效率，尤其是在用户多于项目的情形下尤为显著。
基于项目（Item-Based）的协同过滤算法是常见的另一种算法。与User-Based协同过滤算法不一样的是，Item-Based协同过滤算法计算Item之间的相似度，从而预测用户评分。也就是说该算法可以预先计算Item之间的相似度，这样就可提高性能。Item-Based协同过滤算法是通过用户评分数据和计算的Item相似度矩阵，从而对目标Item进行预测的。

人话：
先根据现有用户历史浏览产品信息，计算出贡献矩阵，根据矩阵计算项目相似度（这就是模型了）。然后来了个新用户，这个新用户浏览了一些产品，系统会推荐剩下的与浏览的产品相似的产品。

2.2 相似度计算方法

和User-Based协同过滤算法类似，需要先计算Item之间的相似度。并且，计算相似度的方法也可以采用皮尔逊关系系数或者余弦相似度，这里给出一种电子商务系统常用的相似度计算方法，即基于物品的协同过滤算法，其中相似度计算公式如下所示：
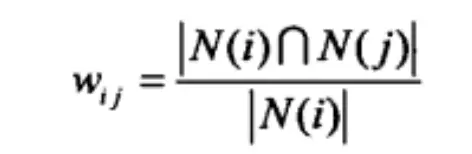
image.png

这里，分母|N(i)|是喜欢物品i的用户数，而分子|N(i)∩N(j)|是同时喜欢物品i和j的用户，但是如果物品j很热门，就会导致Wij很大接近于1。因此避免推荐出热门的物品，我们使用下面的公式：
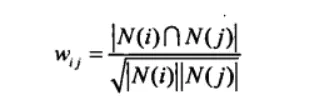
image.png
从上面的定义可以看出，在协同过滤中两个物品产生相似度是因为他们共同被很多用户喜欢，也就是说每个用户都可以通过他们的历史兴趣列表给物品“贡献”相似度。
计算物品相似度首先建立“用户-物品倒排表”（即对每个用户建立一个包含他喜欢的物品的列表），然后对每个用户，将他物品列表中的物品两两在共现矩阵中加1。【贡献矩阵 理解成 共现矩阵 可能会容易一点。共同出现的矩阵】

2.3 用户-物品倒排表与共现矩阵

计算相似度，我们需要用户-物品倒排表：
举例：若有5个用户：A，B，C，D，E。五个物品a，b，c，d，e。如下图所示，A用户对应a，b，d这几个物品；B用户对应b，c，e；C用户对应c，d；D用户对应b，c，d；E用户对应a，d。
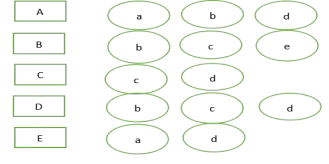
image.png
用户-物品倒排表，如下图所示：
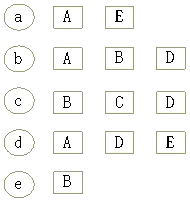
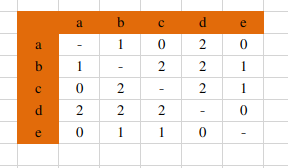
image.png
计算共现矩阵：
下面这张图分为三列，第一列是用户历史信息，第二列是每个用户的 “用户-物品倒排表”， 第三列就是我们需要的共现矩阵。共现矩阵是“用户-物品倒排表”简单相加。共现矩阵的对角线元素全为0，且是实对称稀疏矩阵。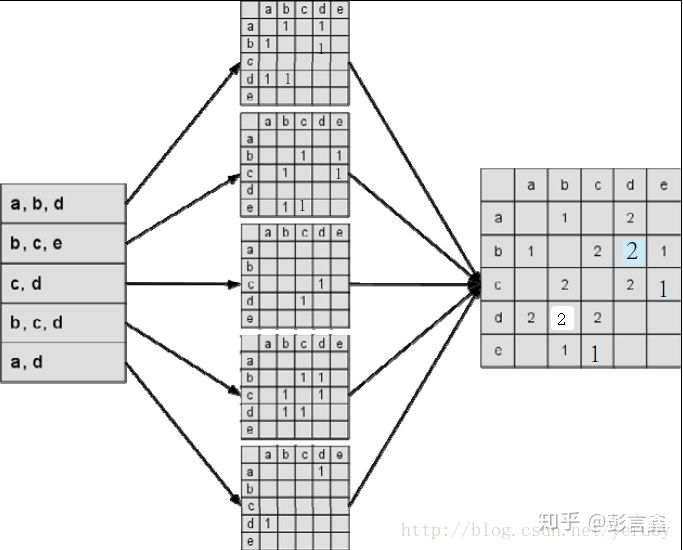
image.png
根据矩阵计算每两个物品之间的相似度wij。

2.4 用户u对于物品j的兴趣

得到物品之间的相似度后，可以根据如下公式计算用户u对于物品j的兴趣：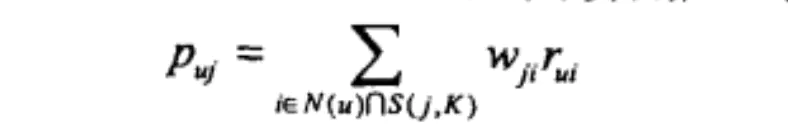
image.png

这里N(u)是用户喜欢的物品的集合，S(j,K)是和物品j最相似的K个物品的集合，wji是物品j和i的相似度，rui是用户u对物品i的兴趣。（对于隐反馈数据集，如果用户u对物品i有过行为，即可令rui=1。）该公式的含义是，和用户历史上感兴趣的物品越相似的物品，越有可能在用户的推荐列表中获得比较高的排名。

当我们看到这里的时候很可能由于自己功底不足，很难看懂公式中的i∈N(u)∩S(j,K)。
我们来看另外一种计算方式：
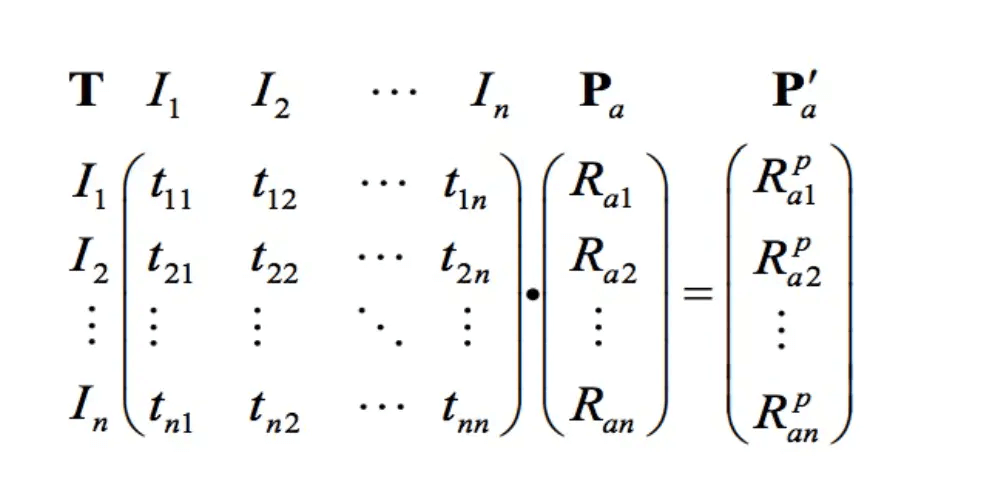
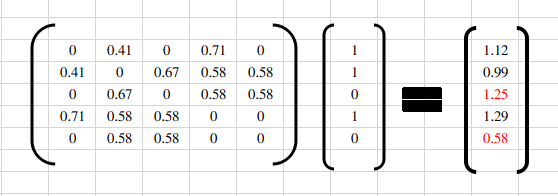
image.png

其中，Pa为新用户对已有产品的向量，T为物品的共现矩阵，得到的P`a为新用户对每个产品的兴趣度。
那么就可以理解上述公式的i∈N(u)∩S(j,K)，我们在下面的例子中详细讲解。

2.5 举例

现有用户的访问的记录如下图所示：
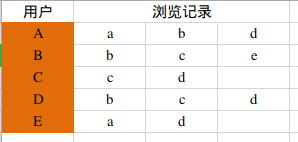
image.png
各个物品喜欢的人数：
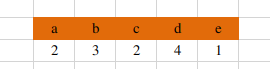
image.png
共现矩阵为(实为相似度计算公式的分子)：
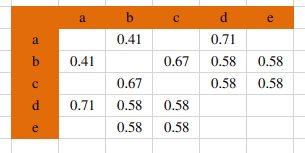
image.png
通过公式计算相似度：
Wa,b = 1 / (根号(2*3)) = 1/根号(6) = 0.41
以此类推：
image.png
此时，来了一个用户F，它浏览了a,b,d三件产品
可以看做向量P
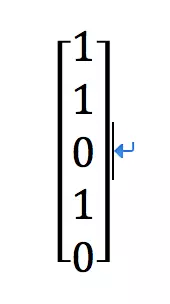
image.png
那么可以得到用户F对产品C （1.25）更有兴趣 ，可以推送。如下图：
image.png

2.6 理解公式i∈N(u)∩S(j,K)

那么现在我们来理解公式i∈N(u)∩S(j,K)：
对于用户F，已经访问了a,b,d，那么，N(u)={a,b,d}；还有两个未访问物品c,e，那么j={c,e}；
当j=c时，对于和物品j最相似的K个物品的集合为{b, d,e}，那么S(j,K)={b,d,e}；得出N(u)∩S(j,K)={b,d},如下图所示：
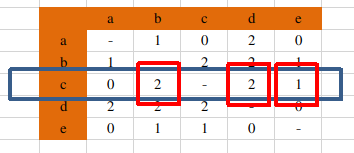
image.png
再来看矩阵相乘中的c行，乘以P，实际上就是上述N(u)∩S(j,K)={b,d}的相似度求和。
同理，e的求法一样