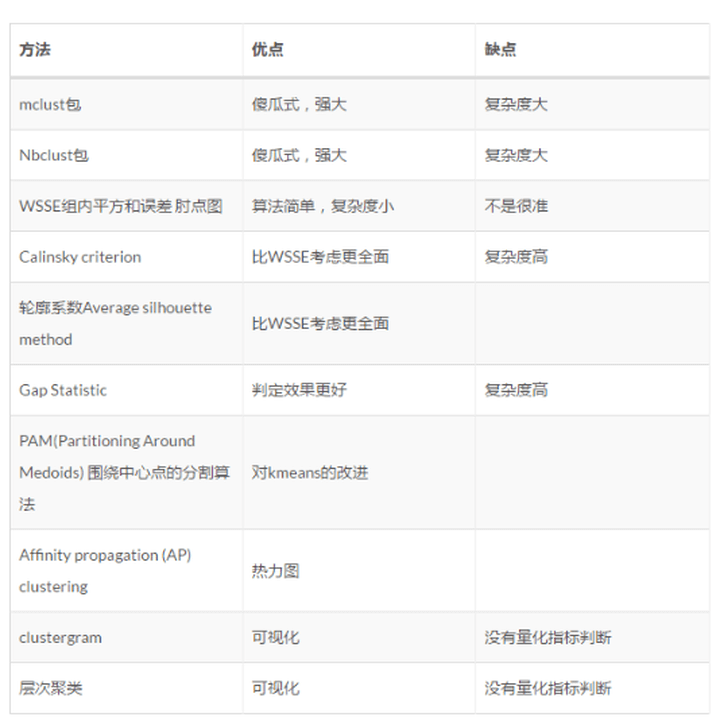
参考https://www.cnblogs.com/think90/p/7133753.html

  1. 组内平方误差和——拐点图（肘部法则SSE）
  2. 轮廓系数

1. 组内平方误差和——拐点图（肘部法则SSE）

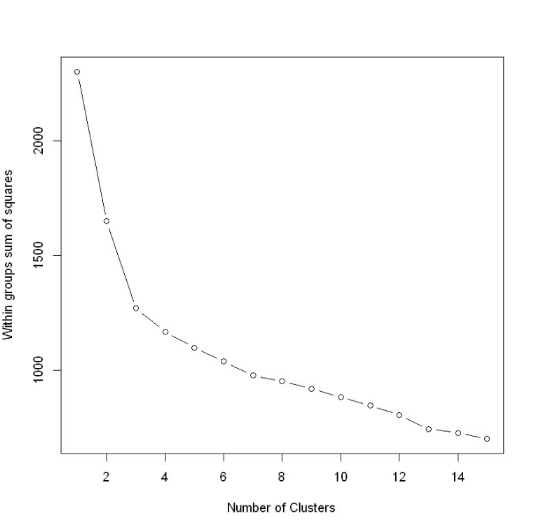
image.png
随着聚类数目增多，每一个类别中数量越来越少，距离越来越近，因此WSS值肯定是随着聚类数目增多而减少的，所以关注的是斜率的变化，但WWS减少得很缓慢时，就认为进一步增大聚类数效果也并不能增强，存在得这个“肘点”就是最佳聚类数目，从一类到三类下降得很快，之后下降得很慢，所以最佳聚类个数选为3。

2. 轮廓系数

轮廓系数是类的密集与分散程度的评价指标。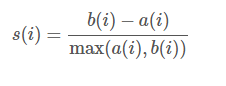
image.png
a(i)是测量组内的样本i在到其它点的平均距离，b(i)是测量组间的样本i到最近不同类别中样本的平均距离，s(i)范围从-1到1，值越大说明组内吻合越高，组间距离越远——也就是说，轮廓系数值越大，聚类效果越好。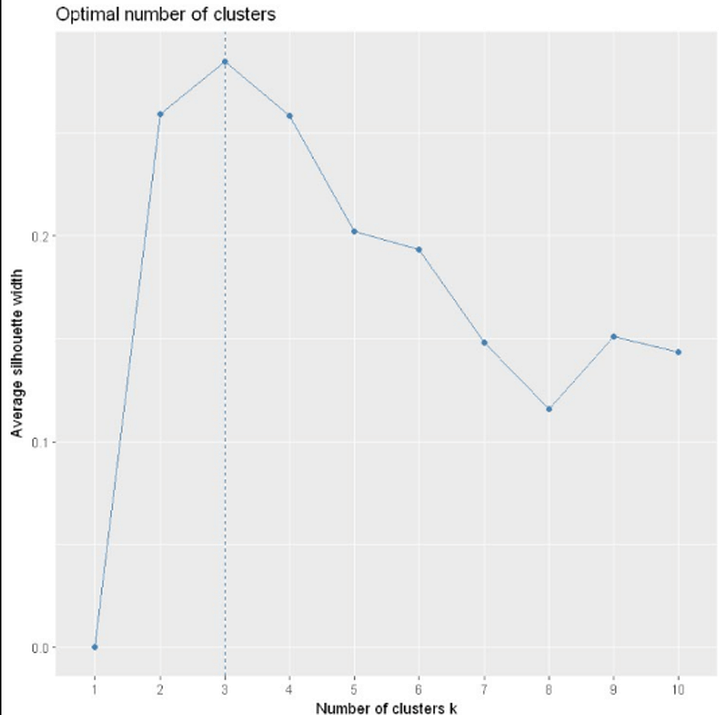
image.png

image.png

3. 实现

参考 https://www.cnblogs.com/feffery/p/12325741.html
我是直接拷贝https://github.com/arvkevi/kneed/blob/master/kneed/knee_locator.py 的实现，这就不用安装kneed模块了。
（输入参数）KneeLocator是kneed中用于检测拐点的模块，其主要参数如下：

x：待检测数据对应的横轴数据序列，如时间点、日期等
y：待检测数据序列，在x条件下对应的值，如x为星期一，对应的y为降水量
S：float型，默认为1，敏感度参数，越小对应拐点被检测出得越快
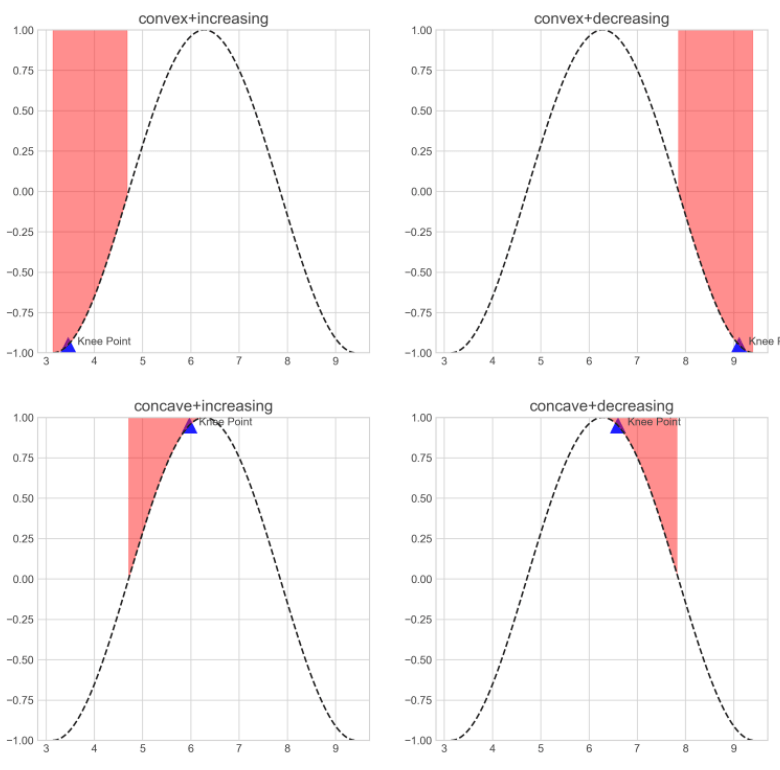
curve：str型，指明曲线之上区域是凸集还是凹集，concave代表凹，convex代表凸
direction：str型，指明曲线初始趋势是增还是减，increasing表示增，decreasing表示减
online：bool型，用于设置在线/离线识别模式，True表示在线，False表示离线；在线模式下会沿着x轴从右向左识别出每一个局部拐点，并在其中选择最优的拐点；离线模式下会返回从右向左检测到的第一个局部拐点

KneeLocator在传入参数实例化完成计算后，可返回的我们主要关注的属性如下：

knee及elbow：返回检测到的最优拐点对应的x
knee_y及elbow_y：返回检测到的最优拐点对应的y
all_elbows及all_knees：返回检测到的所有局部拐点对应的x
all_elbows_y及all_knees_y：返回检测到的所有局部拐点对应的y

  1. import matplotlib.pyplot as plt
  2. from matplotlib import style
  3. import numpy as np
  4. from kneed import KneeLocator
  6. style.use('seaborn-whitegrid')
  8. x = np.arange(1, 3, 0.01)*np.pi
  9. y = np.cos(x)
  11. # 计算各种参数组合下的拐点
  12. kneedle_cov_inc = KneeLocator(x, 
  13.                       y, 
  14.                       curve='convex', 
  15.                       direction='increasing',
  16.                       online=True)
  18. kneedle_cov_dec = KneeLocator(x, 
  19.                       y, 
  20.                       curve='convex', 
  21.                       direction='decreasing',
  22.                       online=True)
  24. kneedle_con_inc = KneeLocator(x, 
  25.                       y, 
  26.                       curve='concave', 
  27.                       direction='increasing',
  28.                       online=True)
  30. kneedle_con_dec = KneeLocator(x, 
  31.                       y, 
  32.                       curve='concave', 
  33.                       direction='decreasing',
  34.                       online=True)
  37. fig, axe = plt.subplots(2, 2, figsize=[12, 12])
  39. axe[0, 0].plot(x, y, 'k--')
  40. axe[0, 0].annotate(s='Knee Point', xy=(kneedle_cov_inc.knee+0.2, kneedle_cov_inc.knee_y), fontsize=10)
  41. axe[0, 0].scatter(x=kneedle_cov_inc.knee, y=kneedle_cov_inc.knee_y, c='b', s=200, marker='^', alpha=1)
  42. axe[0, 0].set_title('convex+increasing')
  43. axe[0, 0].fill_between(np.arange(1, 1.5, 0.01)*np.pi, np.cos(np.arange(1, 1.5, 0.01)*np.pi), 1, alpha=0.5, color='red')
  44. axe[0, 0].set_ylim(-1, 1)
  46. axe[0, 1].plot(x, y, 'k--')
  47. axe[0, 1].annotate(s='Knee Point', xy=(kneedle_cov_dec.knee+0.2, kneedle_cov_dec.knee_y), fontsize=10)
  48. axe[0, 1].scatter(x=kneedle_cov_dec.knee, y=kneedle_cov_dec.knee_y, c='b', s=200, marker='^', alpha=1)
  49. axe[0, 1].fill_between(np.arange(2.5, 3, 0.01)*np.pi, np.cos(np.arange(2.5, 3, 0.01)*np.pi), 1, alpha=0.5, color='red')
  50. axe[0, 1].set_title('convex+decreasing')
  51. axe[0, 1].set_ylim(-1, 1)
  53. axe[1, 0].plot(x, y, 'k--')
  54. axe[1, 0].annotate(s='Knee Point', xy=(kneedle_con_inc.knee+0.2, kneedle_con_inc.knee_y), fontsize=10)
  55. axe[1, 0].scatter(x=kneedle_con_inc.knee, y=kneedle_con_inc.knee_y, c='b', s=200, marker='^', alpha=1)
  56. axe[1, 0].fill_between(np.arange(1.5, 2, 0.01)*np.pi, np.cos(np.arange(1.5, 2, 0.01)*np.pi), 1, alpha=0.5, color='red')
  57. axe[1, 0].set_title('concave+increasing')
  58. axe[1, 0].set_ylim(-1, 1)
  60. axe[1, 1].plot(x, y, 'k--')
  61. axe[1, 1].annotate(s='Knee Point', xy=(kneedle_con_dec.knee+0.2, kneedle_con_dec.knee_y), fontsize=10)
  62. axe[1, 1].scatter(x=kneedle_con_dec.knee, y=kneedle_con_dec.knee_y, c='b', s=200, marker='^', alpha=1)
  63. axe[1, 1].fill_between(np.arange(2, 2.5, 0.01)*np.pi, np.cos(np.arange(2, 2.5, 0.01)*np.pi), 1, alpha=0.5, color='red')
  64. axe[1, 1].set_title('concave+decreasing')
  65. axe[1, 1].set_ylim(-1, 1)
  67. # 导出图像
  68. plt.savefig('图2.png', dpi=300)

image.png