转https://mp.weixin.qq.com/s/Kp_9iQdd1yqZrotaU3R7eA

1. 内容预告

我们知道K最近邻算法（KNN）可以用于查找与目标数据最相似的topk数据，但是K最近邻属于精准搜索，复杂度是线性的，在处理海量数据且数据维度较高时，难以满足对时间性能的要求。

举个例子，做新闻推荐系统，用户点击了一篇文章，如何从海量新闻文本（上亿级别）中找到和这篇文章最相似的10篇新闻。

于是近似最近邻搜索（ANN，Approximate Nearest Neighbor）闪亮登场。

近似最近邻搜索在可接受范围内，牺牲精度以提高检索效率。

局部敏感哈希（locality-sensetive hashing，LSH）就是一种常用的近似最近邻搜索算法。

faiss这个库用C++高效实现了局部敏感哈希，但是这个方法并不是速度最快、内存最省的方法。

下面我们就来看看这个库实现了哪些方法。

本文关注以下四方面的内容：

  • 近似最近邻搜索的方法
  • faiss库中加速计算的方法
  • faiss库中降低内存压力的方法
  • faiss库的索引工厂函数

2. 近似最近邻搜索的方法

近似最近邻搜索的思想是：在海量数据的情况下，不必强求找到最相似的topk个数据，而只要搜索到相似度的确非常高的topk个数据即可，在可接受的范围内，牺牲精度以提高搜索的效率。

近似最近邻搜索一般可以实现两个目标：一是加快查询速度，二是降低内存压力。

那它是怎么实现的呢？

近似最近邻搜索中蕴含了降维和聚类的思想，以下是两种常用的实现方法：

一是基于哈希函数的局部敏感哈希，二是基于向量量化的乘积量化。

2.1 局部敏感哈希

image.png基于哈希的方法，是通过哈希函数把向量变换成二值码(如0101110101)，然后将向量距离近似成二值码距离（如海明距离），从而减少计算距离的时间。

局部敏感哈希就是一种基于哈希的方法，通过选择合适的哈希函数，将高维空间的数据映射到低维空间。

这起到降维的作用。

同时以非常大的概率，将在高维空间中相邻的点，映射到同一个桶（Bucket）中，而不相邻的点，映射到同一个桶的概率很小。

这起到聚类的作用。
在高维空间中相邻的数据，映射到低维空间后，依然保持相邻关系，这与传统的HashTable不同。image.png
image.png

对数据库中的所有数据都进行哈希映射，把所有数据分到不同的桶里面。

过来一条查询数据，将其映射到某个桶内，然后和这个桶内的所有数据计算距离，从而得出topk相似的数据。

这就将在一个超大集合内查找相邻元素的问题，转化为了在一个很小的子集合内查找相邻元素的问题，计算量自然减少了。

2.2 乘积量化

以下对向量量化的解释来自于微软研究院的文章：

向量量化是通过聚类把向量集聚成若干类，每类里面的向量用对应的类中心来近似。 这样子，每个向量只需要用其对应的聚类中心的索引ID来表示，其与查询向量间的距离用其对应的聚类中心与查询向量间的距离来近似。 向量量化带来了两项优势：
（1）向量需要的存储空间变少了，只需保存对应的聚类中心的ID； （2）计算时间减少了，只需要通过聚类中心的索引ID来查询预先计算好的聚类中心与查询向量的距离表格。

这是什么意思？
向量用对应的类中心来近似，那这个类里面的所有向量不就是一样的吗？

错！

乘积量化（PQ，Product Quantization）是向量量化的代表方法，我们来看乘积量化是怎么做的，就能理解上面的话了。

上面说的聚类，可不是把所有的向量进行聚类，而是先把向量切分成若干个区域（类似BERT的Multi-Head的切分），再对每个区域的所有数据进行聚类。

比如数据有1万条，每条数据表示为100维的向量。

把100维向量切分为4个25维的子向量，第1个子向量集合仍然有1万个数据，第2、3、4个子向量集合也有1万个数据。

对于每个子向量集合（1万个数据）聚成K类，得到K个类中心。

每个子向量集合作为一个量化器，可以得到4个量化器（Quantizer）。
image.png那么聚类中心一共是4×K个吗？

错！

聚类中心一共是K^4个。

因为这是乘积量化，而乘积指的是笛卡尔积。

假设集合A={a,b}，集合B={1,2,3,4}，也就是K=2，则两个集合的笛卡尔积为：：
image.png
8个聚类中心，正是K的4次方。

那么向量用对应的聚类中心来近似，又是啥子？

比如一个向量被切分了4个子向量，4个子向量分别属于 a、b、a、b类。

那么该向量就表示为（a_1, b_2, a_3, b_4），也就是用聚类中心的id来表示。

从100维变成了4维，维度降低25倍。

如果这100维数据是float32类型的（32bits），压缩成8bits，那么压缩比为：
(100*32/4)/8=100
为啥你解释得这么细？

因为faiss这个库的乘积量化就是这么干的啊！

以上是前期的准备工作，可以看做是在训练一个模型，构建所有聚类中心的索引（Index）。

模型训练好了，来了一个查询向量，怎么搜索topk相似呢？

这就需要计算查询向量和数据库中某个向量的距离。

论文中有两种计算距离的近似方法：

对称方法（Symmetric distance computation ，SDC）。

非对称方法（Asymmetric distance computation ，ADC）。

对称方法就是指，将查询向量和被查询向量都用聚类中心的id来编码。
查询向量：（a_1, b_2, a_3, b_4）
被查向量：（a_1, a_2, b_3, a_4）

聚类中心两两之间的距离提前计算好了，假如为：

查询向量：（a_1, b_2, a_3, b_4）
被查向量：（a_1, a_2, b_3, b_4）
中心距离：（0, 1, 3, 0）

那么 sum(0,1,3,0)=4，就是查询向量和被查向量的距离。

对应的公式为：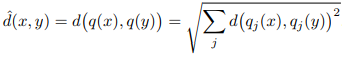
image.png
非对称方法就是指，不需要将查询向量用聚类中心的id来编码，只对被查询向量编码。

将查询向量分为4个子向量后，直接求子向量和被查向量的聚类中心的距离，再加总求和。

查询向量：（1, 2, 3, 4）
被查向量：（a_1, b_2, a_3, b_4）
中心距离：（0, 1, 3, 0）

对应的公式为：
image.png
论文中选择的方法是非对称的方法。

用一句话来总结乘积量化：

乘积量化的本质是将高维向量空间分解为子空间的笛卡尔积，然后分别量化这些子空间。

3. faiss库的使用

3.1 faiss是什么

faiss是Facebook Ai团队开源的一个近似最近邻搜索库，内部用C++高效实现了局部敏感哈希、乘积量化、Kmeans和PCA等算法，在单个服务器的内存中，支持对数十亿的稠密向量进行高效的相似性搜索。

faiss提供了python的API，和numpy进行完美交互。

此外，对一些最常用的算法，支持GPU计算。

github的地址：
https://github.com/facebookresearch/faiss

3.2 faiss的小原理

近似最近邻搜索库，比如faiss、annoy，都有一个核心的概念：Index，意思是索引。

在上面介绍乘积量化的时候，我们说向量可以用其子向量聚类中心的索引来共同表示，所以需要构建聚类中心的索引。

也就是基于聚类中心的id，构建一个倒排索引，key为聚类中心的id，value为向量集合。

比如下图，子向量个数为4，聚成2类，构建的倒排索引如下：
image.png

向量与向量之间对比相似度，不再是通过计算原稠密向量的距离，而是先用聚类中心的索引来表示向量，再计算L2距离或向量内积。

向量1：（a_1, b_2, a_3, b_4）
向量2：（a_1, a_2, b_3, a_4）

构建索引有很多方法，faiss中实现了多种索引结构，在搜索时间、搜索精度、内存消耗等方面进行权衡，使用者各取所需。

3.3 faiss的安装

说了一大堆，终于可以使用faiss了。

我们只安装CPU版就行，先安装好anaconda，再执行以下命令：

  1. conda install faiss-cpu -c pytorch


官网说，安装CPU版需要一个库：BLAS。

我直接执行上面的命令也没报错，可能这个 BLAS 已经装好了。
不可以用pip装，亲测会报错，没有找到解决方式。
可以使用Dockerflie安装

  1. FROM conda/miniconda3:latest 
  3. RUN   conda install -y faiss-cpu -c pytorch -c https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/main/

3.4 faiss的乘积量化

亲测faiss中的乘积量化效果贼好，速度快而且省内存，所以我们直接先来看乘积量化的使用。

首先我们构造备查的向量数据和查询向量。

构造了200万个128维的备查向量，服从正态分布。

向量为float32类型，对应32bits（位），4bytes（字节）。

  1. #coding:utf-8
  2. import time
  3. import numpy as np 
  4. """ 
  5. 1: 向量128维，构造200万个向量，服从正态分布
  6. """
  7. d = 128         
  8. n_data = 2000000  
  9. np.random.seed(0) 
  10. data = []
  11. mu = 3
  12. sigma = 0.1
  13. for i in range(n_data):
  14.     data.append(np.random.normal(mu, sigma, d))
  15. """ 向量为float32类型，即32bits（位数），4bytes（字节）"""
  16. data = np.array(data).astype('float32')

再构造10个查询向量，同样是128维。

  1. """
  2. 2: 构造10个查询向量
  3. """
  4. query = []
  5. n_query = 10
  6. for i in range(n_query):
  7.     query.append(np.random.normal(mu, sigma, d))
  8. query = np.array(query).astype('float32')

再接着构建乘积量化索引

  1. """
  2. 3: 构建索引
  3. """
  4. import faiss
  5. """ 将向量切分为8个子向量，每个向量16维，
  6. 所以m必须能被d整除"""
  7. m = 8
  8. """ 每个子向量集合都聚成100类 """
  9. nlist = 100          
  10. """ 取top10相似向量 """
  11. k = 10
  12. """ 构建量化器 """
  13. start = time.time()
  14. quantizer = faiss.IndexFlatL2(d) 
  15. """ 每个子向量从32bits编码为8bits，
  16. 如果希望加大压缩比率，也可以编码为4bits """
  17. index = faiss.IndexIVFPQ(quantizer, d, nlist, m, 8)
  18. index.train(data)
  19. index.add(data)
  20. """ 个人理解是计算查询向量和100个聚类中心的距离，然后取距离最小的10个类别，
  21. 然后再去这10个类别中找top10相似，类似于beam search，
  22. 因为nprobe=100时，时间消耗等同于没有聚类。
  23. """
  24. index.nprobe = 10
  25. end = time.time()
  26. print("Time usage for train: {} seconds.".format(round((end - start),4)))

参数和方法介绍如下：

m：按照上面乘积量化的介绍，需要将向量切分为多个子向量，我们选择切分为8个子向量。

显然子向量的个数m必须能被向量维度d整除。

nlist：然后把每个子向量集合都聚成100类，也就是文档里面说的划分为100个维诺空间。

乘积量化索引应该用的是Kmeans来聚类。

k：取topk相似的向量。

faiss.IndexIVFPQ：倒排索引（IVF）+PQ编码。

倒排索引把向量用多个聚类中心的id来共同表示，以提高查询效率。

key为聚类中心的id，value为向量集合，如下：
image.png
但是索引中保存了原始向量（128维，32bits），在数据量大时会占用大量内存，甚至造成内存溢出。

于是使用PQ编码对原始向量进行有损压缩，从32bits压缩为8bits或4bits。

测试发现不使用乘积量化，构建好的索引占用了近1G内存，而使用乘积量化，构建好的索引只占用了32M内存。

index.nprobe：在多少个维诺空间中查询。

个人理解是计算查询向量和100个聚类中心的距离，然后取距离最小的10个类别，然后再去这10个类别中找top10相似，类似于beam search。

nprobe越大，查询的精度越高，时间消耗越多，当nprobe=nlist时，时间消耗等同于没有做聚类的。

构建只花了14秒。

  1. Time usage for train: 13.6571 seconds.

索引构建好之后，我们就可以查询topk相似的向量了。

首先我们通过查询在索引中已有的向量，来进行验证：

  1. """
  2. 4: 近似最近邻搜索
  3. """
  4. """ 查询验证 """
  5. start = time.time()
  6. dis, ind = index.search(data[:10], k) 
  7. end = time.time()
  8. print(ind)
  9. print("\nTime usage for search: {} seconds.\n".format(round((end - start),4)))

faiss支持并行查询，可以看到top1相似的向量就是向量本身，10条查询向量同时查询，只花了8ms。
image.png
然后进行真实查询，耗时也是8ms左右。

  1. """ 真实查找 """
  2. start = time.time()
  3. dis, ind = index.search(query, k) 
  4. end = time.time()
  5. print(ind)
  6. print("\nTime usage for search: {} seconds.\n".format(round((end - start),4)))

最后保存索引文件，文件大小只有32m。

  1. """
  2. 5: 保存索引和加载索引
  3. """
  4. faiss.write_index(index, "index_IVFPQ.index")
  5. index = faiss.read_index("index_IVFPQ.index")

3.5 faiss自定义id

在默认情况下，faiss会给添加到索引中的向量分配递增的id。

但实际工作场景中，数据库中的向量已经分配了id，为字符串或者数字。

那么把向量添加到索引中时，就涉及到手动设置向量id的问题。

faiss中的一些索引类型（比如使用了倒排索引IVF的类型）使用add_with_ids方法可以直接自定义id，但必须是int类型，不能为float和字符串。

所以如果数据库中的向量id为字符串，那就需要自己维护一套字符串id到int型id的映射。

  1. """
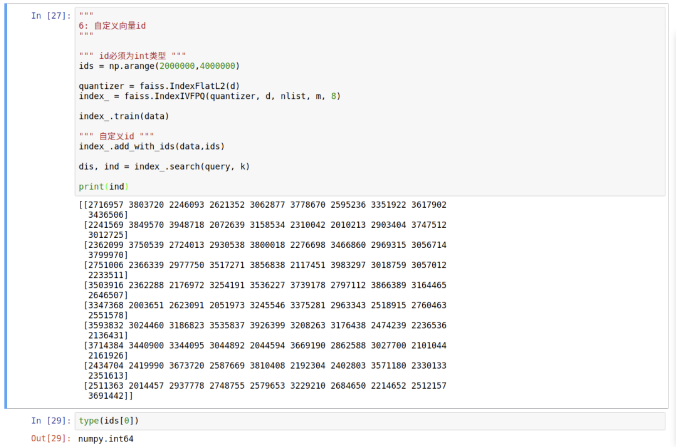
  2. 6: 自定义向量id
  3. """
  4. """ id必须为int类型 """
  5. ids = np.arange(2000000,4000000)
  6. quantizer = faiss.IndexFlatL2(d) 
  7. index_ = faiss.IndexIVFPQ(quantizer, d, nlist, m, 8)
  8. index_.train(data)
  9. """ 自定义id """
  10. index_.add_with_ids(data,ids)
  11. dis, ind = index_.search(query, k) 
  12. print(ind)

可以看到向量的id已经转换过来了。
image.png

3.6 faiss的索引工厂函数

faiss提供了一个index_factory的方法，可以直译为：索引工厂函数。

这个索引工厂函数是用来干嘛的呢？

faiss库在构建索引时，为了进一步提高计算效率或减少内存压力，会综合运用更多的算法。

比如上面已经用了倒排索引+PQ编码，还可以预先用PCA对向量进行降维。

如此一来，在写代码的时候，我们就需要分三步：

首先进行PCA降维（数据预处理），然后倒排（聚类），最后PQ编码（编码）。

为了省事，干脆直接用一个字符串，把数据预处理、聚类、编码的方法和参数拼接在一起，放入索引工厂函数中，一行代码就生成了复合索引。

下面就用索引工厂函数来构建索引：

  • 数据预处理：OPQ16_64，意思是用OPQ把向量降为64维，分为16类。
  • 聚类：IMI2×8，这个没看懂，官网说是构建了65536个倒排索引。
  • 编码：PQ16，意思是把向量压缩到16字节。原先是 128*4=512字节，这压缩了32倍。
  1. """
  2. 7：索引工厂
  3. """
  4. index_fac = faiss.index_factory(d,"OPQ16_64,IMI2x8,PQ16") 
  5. start = time.time()
  6. index_fac.train(data)
  7. index_fac.add(data)
  8. end = time.time()
  9. print("\nTime usage for train: {} seconds.\n".format(round((end - start),4)))
  10. start = time.time()
  11. dis, ind = index_fac.search(data[:10], 10)  # 真实查询
  12. end = time.time()
  13. print(ind)
  14. print("\nTime usage for search: {} seconds.\n".format(round((end - start),4)))

可以看到训练慢了很多，81秒，但是查询快多了，0.4ms。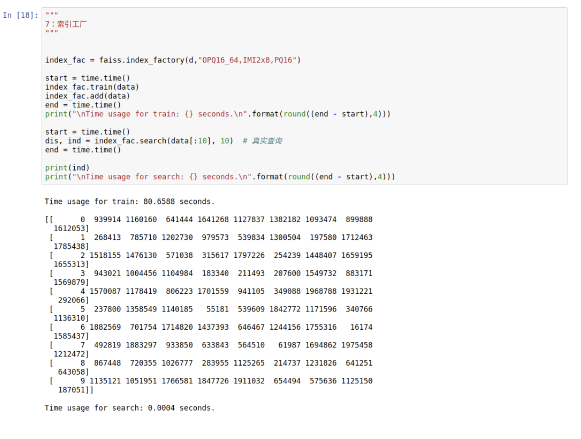
image.png
在这个文件中可以看到很多组合，可以根据实际情况去选择。

https://github.com/facebookresearch/faiss/blob/master/demos/demo_auto_tune.py

  1. # indexes that are useful when there is no limitation on memory usage
  2. unlimited_mem_keys = [
  3.     "IMI2x10,Flat", "IMI2x11,Flat",
  4.     "IVF4096,Flat", "IVF16384,Flat",
  5.     "PCA64,IMI2x10,Flat"]
  6. # memory limited to 16 bytes / vector
  7. keys_mem_16 = [
  8.     'IMI2x10,PQ16', 'IVF4096,PQ16',
  9.     'IMI2x10,PQ8+8', 'OPQ16_64,IMI2x10,PQ16'
  10.     ]
  11. # limited to 32 bytes / vector
  12. keys_mem_32 = [
  13.     'IMI2x10,PQ32', 'IVF4096,PQ32', 'IVF16384,PQ32',
  14.     'IMI2x10,PQ16+16',
  15.     'OPQ32,IVF4096,PQ32', 'IVF4096,PQ16+16', 'OPQ16,IMI2x10,PQ16+16'
  16.     ]

3.7 faiss的精确搜索

我们可以用faiss中的精确搜索作为baseline，来对比以上近似搜索的计算效率和计算精度。

IndexFlatL2索引类型是最简单的精确搜索类型，没有训练的环节，只需要把向量添加到索引中。

查询时，计算查询向量和所有被查询向量的L2距离，进行精确搜索。

查找耗时600ms左右。

  1. """
  2. 8：精确查找作为baseline，进行对比
  3. """
  4. index_exact = faiss.IndexFlatL2(d)  
  5. """ 不需要训练 """
  6. index_exact.add(data)
  7. start = time.time()
  8. dis, ind = index_exact.search(data[:10], 10)
  9. end = time.time()
  10. print(ind)
  11. print("\nTime usage for search: {} seconds.\n".format(round((end - start),4)))

3.8 faiss的索引类型

上面介绍的倒排索引+PQ编码只是faiss中的一个索引类型，faiss中的其他索引类型可以在这个页面查看。

https://github.com/facebookresearch/faiss/wiki/Faiss-indexes

以下是部分索引类型。

| Method | Class name | index_factory | Main parameters | Bytes/vector | Exhaustive | Comments | | Exact Search for L2 | IndexFlatL2 | "Flat" | d | 4*d | yes | brute-force | | —- | —- | —- | —- | —- | —- | —- | | Exact Search for Inner Product | IndexFlatIP | "Flat" | d | 4*d | yes | also for cosine (normalize vectors beforehand) | | Hierarchical Navigable Small World graph exploration | IndexHNSWFlat | ‘HNSWx,Flat|d,M|4d + x M 2 4| no | | | Inverted file with exact post-verification |IndexIVFFlat|“IVFx,Flat”|quantizer,d,nlists,metric|4d + 8| no | Takes another index to assign vectors to inverted lists. The 8 additional bytes are the vector id that needs to be stored. | | Locality-Sensitive Hashing (binary flat index) |IndexLSH| - |d,nbits|ceil(nbits/8)| yes | optimized by using random rotation instead of random projections | | Scalar quantizer (SQ) in flat mode |IndexScalarQuantizer|“SQ8”|d|d| yes | 4 and 6 bits per component are also implemented. | | Product quantizer (PQ) in flat mode |IndexPQ|“PQx”,“PQ”x”x”nbits|d,M,nbits|ceil(M nbit / 8)| yes | | | IVF and scalar quantizer |IndexIVFScalarQuantizer| "IVFx,SQ4" "IVFx,SQ8" |quantizer,d,nlists,qtype| SQfp16: 2 *d+ 8, SQ8:d+ 8 or SQ4:d/2+ 8 | no | Same as theIndexScalarQuantizer| | IVFADC (coarse quantizer+PQ on residuals) |IndexIVFPQ|“IVFx,PQ”y”x”nbits|quantizer,d,nlists,M,nbits|ceil(M * nbits/8)+8| no | | | IVFADC+R (same as IVFADC with re-ranking based on codes) |IndexIVFPQR|“IVFx,PQy+z”|quantizer,d,nlists,M,nbits,M_refine,nbits_refine|M+M_refine+8` | no | |

可见，faiss也实现了局部敏感哈希（IndexLSH），但是感觉不太重视。

测试也发现在提高计算效率和减缓内存压力方面，局部敏感哈希都比乘积量化逊色。

好了，faiss这个库里面的内容还比较丰富，其他更深入的内容就等以后需要再研究了。

这个demo已经上传至github。

https://github.com/DengYangyong/faiss_demo

4. 参考资料

1：《一文尽览近似最近邻搜索中的哈希与量化方法》
2：《Product Quantization for Nearest Neighbor Search》

3：https://github.com/liqima/faiss_note
4：https://github.com/facebookresearch/faiss/wiki