目标函数、损失函数、代价函数的区别

总结：

• 损失函数就是代价函数
• 对于目标函数来说在有约束条件下的最小化就是损失函数
• 经验风险： 关于训练集的平均损失称作经验风险，
• 结构风险：自变量次数过高带来过拟合的风险，通过l1、l2正则化来缓解。
• 我们最终的优化函数是： ，即最优化经验风险和结构风险，而这个函数就被称为目标函数。

链接：https://www.zhihu.com/question/52398145/answer/209358209

首先给出结论：损失函数和代价函数是同一个东西，目标函数是一个与他们相关但更广的概念，对于目标函数来说在有约束条件下的最小化就是损失函数（loss function）。
举个例子解释一下:（图片来自Andrew Ng Machine Learning公开课视频）

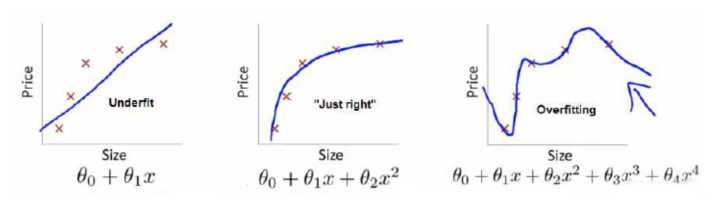
上面三个图的函数依次为 , , 。我们是想用这三个函数分别来拟合Price，Price的真实值记为 。
我们给定 ，这三个函数都会输出一个 ,这个输出的 与真实值 可能是相同的，也可能是不同的，为了表示我们拟合的好坏，我们就用一个函数来度量拟合的程度，比如：
，这个函数就称为损失函数(loss function)，或者叫代价函数(cost function)。损失函数越小，就代表模型拟合的越好。
那是不是我们的目标就只是让loss function越小越好呢？还不是。
这个时候还有一个概念叫风险函数(risk function)。风险函数是损失函数的期望，这是由于我们输入输出的 遵循一个联合分布，但是这个联合分布是未知的，所以无法计算。但是我们是有历史数据的，就是我们的训练集， 关于训练集的平均损失称作经验风险(empirical risk)，即 ，所以我们的目标就是最小化 ，称为经验风险最小化。
到这里完了吗？还没有。
如果到这一步就完了的话，那我们看上面的图，那肯定是最右面的 的经验风险函数最小了，因为它对历史的数据拟合的最好嘛。但是我们从图上来看 肯定不是最好的，因为它过度学习历史数据，导致它在真正预测时效果会很不好，这种情况称为过拟合(over-fitting)。
为什么会造成这种结果？大白话说就是它的函数太复杂了，都有四次方了，这就引出了下面的概念，我们不仅要让经验风险最小化，还要让结构风险最小化。这个时候就定义了一个函数 ，这个函数专门用来度量模型的复杂度，在机器学习中也叫正则化(regularization)。常用的有 , 范数。
到这一步我们就可以说我们最终的优化函数是： ，即最优化经验风险和结构风险，而这个函数就被称为目标函数。
结合上面的例子来分析：最左面的 结构风险最小（模型结构最简单），但是经验风险最大（对历史数据拟合的最差）；最右面的 经验风险最小（对历史数据拟合的最好），但是结构风险最大（模型结构最复杂）;而 达到了二者的良好平衡，最适合用来预测未知数据集。