统一名词：
行：样本
列：特征
特征：将特征、因素、变量等统称为特征。特征分为连续型特征、类别型特征、向量型特征（只在NLP中考虑）。
label：目标对象，最终分析的对象、预测对象等
数据集：分为两部分五个含义

• 特征
  • 时间特征
  • 连续型特征
  • 类别型特征
• label
  • 连续型特征
  • 类别型特征

概述

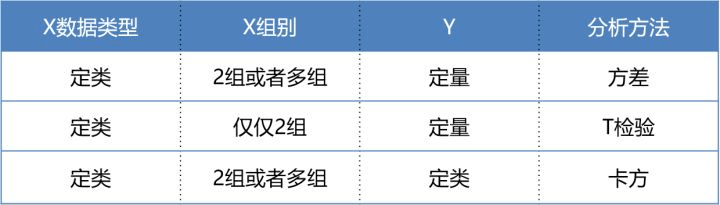
从数据属性上区分三大分析方法的适用范围，数据属性指数据是类别特征还是连续型特征。这里将X作为特征，Y作为label，两者属性未定。

• F检验（方差齐性检验）：X作为类别特征，Y作为连续型特征。将Y以X为准进行分组，这样可以研究每个类别的统计量是否有差异及差异情况。例如研究三组学生（X）的智商平均值（Y）是否有显著差异。
• T检验：X作为类别特征，Y作为连续型特征。也可使用T检验进行差异对比。T检验与单因素方差分析的区别在于T检验只能对比两组数据的差异。
• 卡方检验：X和Y均为类别特征，可对比差异性。

方差分析与假设检验的区别和联系

1. 假设检验

   不管是t检验、z检验、卡方检验、F检验等，都是分子比分母，即用要考察的差异(或波动)与误差的波动进行比较。实质是看原始信号是否显著大于噪声(信噪比)。严格来说，假设检验是检验某种差异的显著性，是从考察的目的上来说的，而非方法。
   不显著就是H0，显著就不是H0(例如H1)。

2. 方差分析

方差分析包含F检验，广义上还包括方差分量的比较，都是将因素水平的效应或差异与误差进行比较，都有显著性检验的功能，所以可以用于假设检验。
双样本比较时，方差分析与t检验是等价的。因为这里F检验与t检验是等价的(F统计量等于t统计量的平方)。也就是说，t检验可以看做最简单情况的方差分析。
通常，t检验适用于单/双样本，方差分析则用于多样本。

单/多因素方差分析

• 单因素方差分析

是用来研究一个控制变量的不同水平是否对观测变量产生了显著影响。通俗地讲就是分析变量x的变化对变量y的影响的显著性，所以一般变量之间存在某种影响关系的，验证一种变量的变化对另一种变量的影响显著性的检验。如以下所说的方差分析、t检验、卡方检验。

• 多因素方差分析

即分析多种因素对某一变量的影响有多大的统计分析。而协方差分析是多种影响因素下，在不考虑某一种因素下，其他因素对该变量的影响有多大。比如，玉米的销量、玉米的价格、爆米花的价格（例子不是很好，但大概就是这个意思，就是a对b有相应，b又对c有影响，但a对c不一定有影响），就是爆米花的价格越高，那么玉米的销量也是 越多的，所以它们之间成正比关系。但这显然是没有相关性的。因为爆米花的价格和玉米的销量均和玉米的温度有关，针对这类问题的分析时要用协方差分析。

方差分析(ANOVA)

概念

方差分析和F检验是同义词，从定义上看，方差分析是一种将样本方差分配到不同来源的过程，判定方差在组间和组内是否（明显）具有区别的一种方法。如果组内差异相对于组间差异较小，则可以推断出组与组之间是有明显差异的。简单来说就是看看两组或几组样本是不是来自同一个总体。

作用

   评估因素对目标变量是否有显著影响。如果有显著影响，则可以作为分类的一个重要特征。

同时也可用于对聚类分析效果的判断。在得到聚类类别之后，通过方差分析去对比不同类别的差异，如果全部呈现出显著性差异，以及研究人员结合专业知识可以对类别进行命名时，则说明聚类效果较好。

思路转换（对标机器学习）

一般方差分析教程用相似/相同的对象产生的数据进行讲解，称这些对象产生的数据称为样本。需要做转换的是，将相似/相同的对象换成不同的对象（就是我们的特征），这样我们的特征就是方差分析中的样本。这样就可以用方差分析进行分析了。
一般教程：

下面我们用一个简单的例子来说明方差分析的基本思想： 如某克山病区测得11例克山病患者和13名健康人的血磷值（mmol/L）如下： 患者：0.84 1.05 1.20 1.20 1.39 1.53 1.67 1.80 1.87 2.07 2.11 健康人：0.54 0.64 0.64 0.75 0.76 0.81 1.16 1.20 1.34 1.35 1.48 1.56 1.87 问该地克山病患者与健康人的血磷值是否不同？

思路转换：

将上述的患者视为一个特征，健康人作为另一个特征。 应用于我自身体系，则将一个类别特征作为一个特征，连续型label作为另一个特征，进行方差分析，探索该类别特征对label的影响程度。

应用前提

正态性检验

方差分析要求Y项满足需要正态性。

不满足正态性

如果出现数据不满足正态性的情况：
①可以进行对数处理：即使用【生成变量】功能对Y项进行转换，使数据呈现出正态性。但转换后的数据分析结果不好解释。
②使用非参数检验：如果没有呈现出正态性特质，可使用非参数检验进行分析。
③直接使用方差分析：参数检验的检验效能高于非参数检验，比如方差分析为参数检验，所以很多时候即使数据不满足正态性要求也使用方差分析。

方差齐性检验

检验结果主要关注P值，即p <0.05,代表数据呈现出显著性，说明不同组别数据波动不一致，即说明方差不齐；反之，**p>0.05，说明方差齐性。**

不满足方差齐性

理论上讲，单因素方差分析应该首先满足方差齐性，但在实际研究过程中，较多数据出现方差不齐现象，可以将分类数据X进行重新组合，或对Y取对数等处理。
如果仍然不满足方差齐性，可使用非参数检验。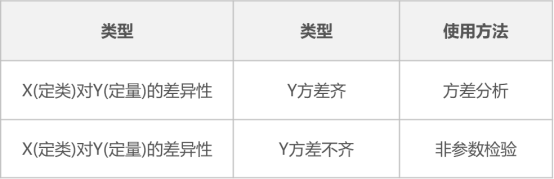

另外，如果研究的分类数据为两类，可以考虑使用独立样本T检验代表方差分析，避免方差不齐无法分析的尴尬。

sklearn实现及解释

摘选自官网iris例子，首先对iris数据集加入扰动，再进行方差分析。
iris数据集是一共包含150个样本，分为3类，每类50个数据，每个数据包含4个属性。可通过花萼长度，花萼宽度，花瓣长度，花瓣宽度4个属性预测鸢尾花卉属于（Setosa，Versicolour，Virginica）三个种类中的哪一类。不太符合应用条件，但将在sklearn中，将方差分析分成了两部分，使得分类问题可以用f_classif，回归问题使用 f_regression【这就是符合原理论的方法】。
这里因为是分类问题，所以使用f_classif。代码格式是一致的，将f_classif换成f_regression也可以执行完。

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.feature_selection import  f_classif
X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=0)
X_indices = np.arange(X.shape[-1])
selector_F,selector_p_value  = f_classif(X_train, y_train)
selector_F,selector_p_value
>>>
(array([ 95.00148955,  37.25014272, 763.24689976, 765.6350149 ]),
 array([1.30445334e-24, 4.69398374e-13, 7.86826504e-65, 6.71208699e-65]))

已经得到了结果，结果有两个值：f值和p-value。但没有进行选择，是因为需要用到sklearn.feature_selection.SelectKBest类来进行选择。用法是：

SelectKBest(f_classif, k=4)
# 具体用法再最后讲解。

函数返回值f值

为了解释方便，这里用模拟场景和数据进行。
我们开发出了一种降血压的药，需要检验这个降血压药品的药效如何。我们就做了如下实验，给定不同剂量，分别是0，1，2，3，4这四个级别的剂量（0剂量表示病人服用了安慰剂），给4组病人服用，在一定时间后测量病人的血压差，在得到数据以后。我们要问，这种新药是不是有显著药效，也就是说病人的血压差是不是显著的不等于0。
数据如下：

我们得到了5个总体 ，这五个总体的均值为，我们假设是：

继而构造检验统计量，分别是组间和组内离差，这个统计量服从，式中，也就是总样本数，是总体个数。在我们这个例子中， ，那么这个统计量服从分布。当这个统计量比较大的时候，也就是超过时，我们拒绝零假设，即认为几个中至少有一个不为0，即认为新药有显著的改变血压。
举这个例子是为了说明值这个统计量最初的目的，在这个例子中，是为了检验：在不同的药剂量下，血压差是不是有显著的差异。那么我们再抽象一下，方差分析的目的是：在随机变量的不同水平下，检验某个变量是不是有显著的变化。
似乎可以隐隐的感受到，这似乎是在说变量和之间的相关性。

前面做了那么多铺垫，终于进入正题了。前面提到利用值这个检验统计量，可以判断假设是否成立：值越大，大到一定程度时，就有理由拒绝零假设，认为不同总体下的均值存在显著差异。
那么在机器学习的分类问题中，怎么理解呢？
我们可以把样本所属的不同的类别视作不同的总体，假设是个二分类问题，我们要考虑特征。那么，如果这个特征对预测类别很大的帮助，它必然存在这样一种特征：
当样本属于正类时，会取某些特定的值（视作集合），当样本属于负类时，会取另一些特定的值()。
我们当然希望集合与呈现出巨大差异，这样特征对类别的预测能力就越强。落实到刚才的方差分析问题上，就变成了我们需要检验假设，我们当然希望拒绝，所以我们希望构造出来的值越大越好。也就是说值越大，我们拒绝的把握也越大，我们越有理由相信，越有把握认为集合与呈现出巨大差异，也就说这个特征对预测类别的帮助也越大！
所以我们可以根据样本的某个特征的值来判断特征对预测类别的帮助，ff值越大，预测能力也就越强，相关性就越大，从而基于此可以进行特征选择。
另外，我们也可以利用f_calssif方法来计算两个特征之间的相关性，前提是其中一个变量是离散型的类别变量。

函数返回值p-value

如果你参考了这个方法的API，会看到这个方法返回两个变量，一个是f值，还有一个是p-value，这个p-value就是用于检验特征与变量之间相关性的，假设你给出α值（常常取0.05，0.01），如果你的p-value小于α，那就有把握认为，这个特征和预测变量y之间，具有相关性。比方说你取α=0.05，这就意味着你有95%（也就是1-α）的把握认为，这个特征和预测变量y之间存在相关性。

下面的就不多说，代码其实都一样，返回结果也都是f值和p-value。

卡方检验

sklearn实现

from sklearn.feature_selection import chi2  # 仅用于分类

案例1

案例来源：链接
检验一颗骰子是否不均匀。测试一共丢了902次，结果如下表
假设这颗色子是正常均匀的，那么每次丢色子，每一点出现的可能性都是1/6，所以理论上每一点出现的次数应该都是：150.33=902/6次。如下表：我们把每一点实际出现的次数与理论情况下应该出现的次数做一个对比，其中实际观察次数用A表示，理论次数用T表示：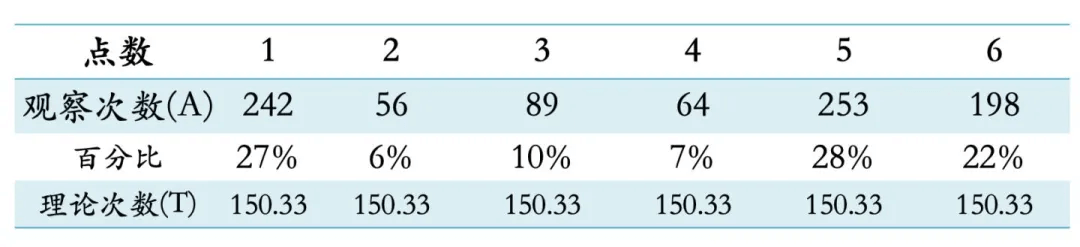

采用假设检验的标准语言来验证就是：
H0：这颗色子是均匀公平，每一点出现的可能性都为1/6；
H1：这颗色子不是均匀公平的，每一点点数出现的概率不都相同；
如果H0假设成立，那么“观察次数”和“理论次数”之间不会差很多；可是如果两者的差距过大，达到我们规定的某个水平，就认为在H0假设成立的情况下是不会出现的，此时就会拒绝原假设，即认为这个色子不是均匀的。
那怎么来计算这个差呢？
依照我们讲标准差的思路，如果直接将实际情况的点数与理论情况点数相减再加和取平均数，基本会得到0的结果，没有什么意义，而取绝对值运算又不方便，所以还是得通过平方。这就是卡方中平方的由来。

上面这个计算公式，A代表“实际频数”，T代表“理论频数”。
如果把这个公式应用到小金丢色子的例子，就会得到：

卡方值为274.92，其对应的P值小于0.01，也就意味着，如果原假设成立（色子没问题），那么“理论与现实”出现这么大的差距的可能低于5%，我们认为这是不可能，因此，要拒绝原假设，认为“色子有问题”。

案例2

卡方检验最常用的是检验两个率是否一致，对照上述“丢色子”的例子，我们会先假设这两个率（注意是指总体率）相等，通过相等的总体率，再反推理论发生的频数，然后计算实际的观察频数与理论频数的卡方值来判断差距是否足够大，从而决定假设是否可以被拒绝。
下面以新冠肺炎为例，说明一下卡方检验的应用。
为比较A、B两个城市新冠肺炎病例的检出情况，分别随机抽取A地377人，B地301人，进行核酸检测。结果见下表（数据纯属虚构），现判断两个城市的新冠肺炎检出率是否相同？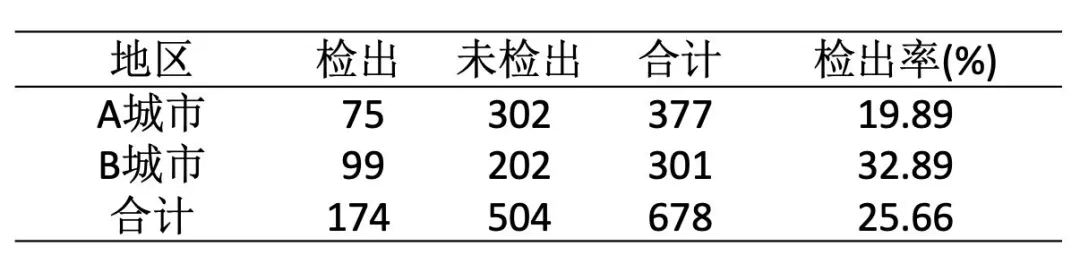

如上表，A地的检出率是19.89%；B地的检出率是32.89%，卡方检验就要来判断这两个样本率所代表的总体率是否相等。
现在我们假设它们相等，那怎么计算理论频数呢？
此时就需要用到“合计检出率——25.66% “来算，这个数据就相当于上述色子例子中的1/6，是一个标准。
所以，如果两城市新冠肺炎检出率没有区别，且大概都为25.66%，那理论上A地会检出多少例呢？96.75（37725.66%），而未检出的就为280.25（377-96.75）。
同理，B地会检出77.25（30125.66%），未检出的就为223.75（301-77.25）。
现在我们就得到了各城市检出与未检出的理论频数，从而就能计算卡方值。

该卡方值对应的P值小于0.05，所以可以认为A、B两个城市新冠肺炎的检出率不一致，B地检出率更高，感染情况更严重。

互信息

sklearn实现

sklearn.feature_selection.mutual_info_classif
sklearn.feature_selection.mutual_info_regression

真*特征选择

上述的例子只是计算了f值和p-value，但没有进行选择特征的操作，一般我们使用sklearn.feature_selection.SelectKBest类来进行选择。用法是：

SelectKBest(f_classif, k=4)
f_classif可以换成上述那些检验的类。

结合管道就有

import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
from sklearn.svm import LinearSVC
from sklearn.pipeline import make_pipeline
from sklearn.feature_selection import SelectKBest, f_classif
X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split( X, y, stratify=y, random_state=0)
clf_selected = make_pipeline(SelectKBest(f_classif, k=4), MinMaxScaler(), LinearSVC())
clf_selected.fit(X_train, y_train)
print('单变量特征选择后的分类精度: {:.3f}'
      .format(clf_selected.score(X_test, y_test)))
svm_weights_selected = np.abs(clf_selected[-1].coef_).sum(axis=0)
svm_weights_selected /= svm_weights_selected.sum()
print("计算每个特征的权重:",svm_weights_selected)
>>> 单变量特征选择后的分类精度: 0.868
>>> 计算每个特征的权重: [0.07317268 0.26756831 0.29844457 0.36081444]

例子

举一个简单的例子：
某电信运营商，面临增量不增收的困境，想弄明白哪些因素有可能会影响客户的消费水平（也就是说，哪些因素与费用有相关性），以及哪些因素与客户流失有相关性，于是收集了如下的表格，请分析并给出结论。

从方法的适用场景，可知：
1） 如果要评估收入对于基本费用的相关性，则可用相关性分析。
2） 如果要评估婚姻状况对于基本费用的相关性，则可用方差分析。
3） 如果要评估教育水平对于客户流失的相关性，则可用列联分析、卡方检验。