转 https://blog.csdn.net/pengchengliu/article/details/80932232
梯度下降算法的公式非常简单，”沿着梯度的反方向（坡度最陡）”是我们日常经验得到的，其本质的原因到底是什么呢？为什么局部下降最快的方向就是梯度的负方向呢？也许很多朋友还不太清楚。没关系，接下来我将以通俗的语言来详细解释梯度下降算法公式的数学推导过程。

下山问题

假设我们位于黄山的某个山腰处，山势连绵不绝，不知道怎么下山。于是决定走一步算一步，也就是每次沿着当前位置最陡峭最易下山的方向前进一小步，然后继续沿下一个位置最陡方向前进一小步。这样一步一步走下去，一直走到觉得我们已经到了山脚。这里的下山最陡的方向就是梯度的负方向。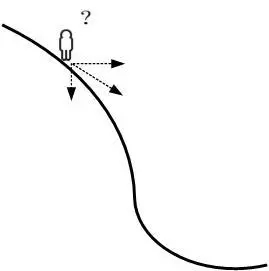

首先理解什么是梯度？通俗来说，梯度就是表示某一函数在该点处的方向导数沿着该方向取得较大值，即函数在当前位置的导数。

其中，θo是自变量参数，即下山位置坐标，η是学习因子，即下山每次前进的一小步（步进长度），θ是更新后的θo，即下山移动一小步之后的位置。

一阶泰勒展开式

这里需要一点数学基础，对泰勒展开式有些了解。简单地来说，一阶泰勒展开式利用的就是函数的局部线性近似这个概念。我们以一阶泰勒展开式为例：

不懂上面的公式？没有关系。我用下面这张图来解释。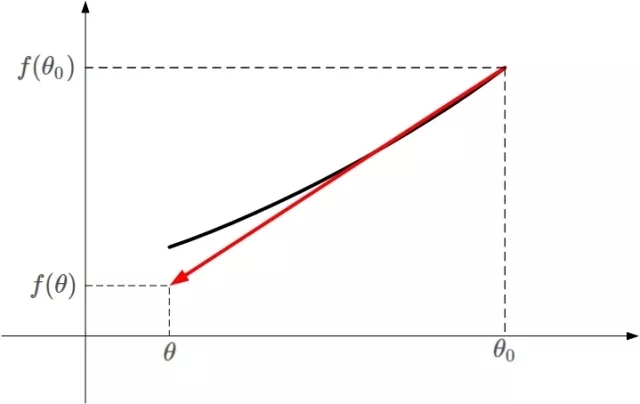

凸函数f(θ)的某一小段[θo,θ]由上图黑色曲线表示，可以利用线性近似的思想求出f(θ)的值，如上图红色直线。该直线的斜率等于f(θ)在θo处的导数。则根据直线方程，很容易得到f(θ)的近似表达式为：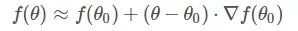

这就是一阶泰勒展开式的推导过程，主要利用的数学思想就是曲线函数的线性拟合近似。

梯度下降数学原理

知道了一阶泰勒展开式之后，接下来就是重点了！我们来看一下梯度下降算法是如何推导的。

反方向 原理

想要两个向量的乘积小于零，我们先来看一下两个向量乘积包含哪几种情况：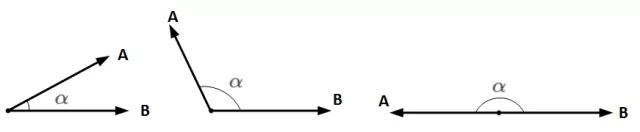

A和B均为向量，α为两个向量之间的夹角。A和B的乘积为：

学习速率

前面也说过学习速率的问题，对于梯度下降算法，这应该是一个最重要的超参数。如果学习速率设置得非常大，那么训练可能不会收敛，就直接发散了；如果设置的比较小，虽然可以收敛，但是训练时间可能无法接受；如果设置的稍微高一些，训练速度会很快，但是当接近最优点会发生震荡，甚至无法稳定。不同学习速率的选择影响可能非常大，如图3所示。

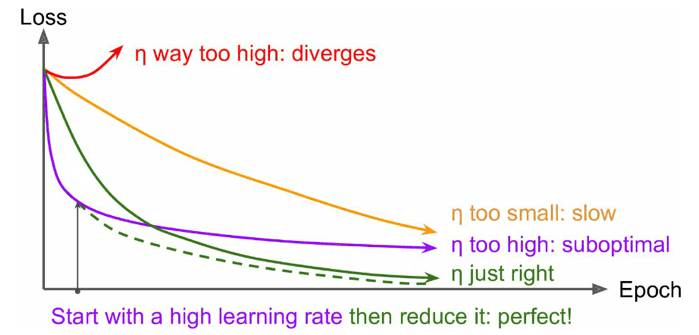
图3 不同学习速率的训练效果

理想的学习速率是：刚开始设置较大，有很快的收敛速度，然后慢慢衰减，保证稳定到达最优点。所以，前面的很多算法都是学习速率自适应的。除此之外，还可以手动实现这样一个自适应过程，如实现学习速率指数式衰减：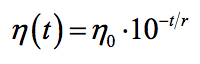

总结

我们通过一阶泰勒展开式，利用线性近似和向量相乘最小化的思想搞懂了梯度下降算法的数学原理。