残差网络

误差：观测值和真实值的差
残差：观测值和预测值的差
网络退化：用残差网络
过拟合：用Dropout
大话残差网络：在深层网络中，每两层视为一个浅层网络。我们期待浅层网络的输出等于输入（即神经网络拟合出这个结果，但很难），从提出思想理解为什么要期待这个结果。为了这个期待结果，于是我们在浅层网络的输出上加上浅层网络的输入，这样神经网络就可以轻松达到这个结果。

1. 残差网络的提出思想

如图 1 所示，在训练集上，传统神经网络越深效果不一定越好。而 Deep Residual Learning for Image Recognition 这篇论文认为，理论上，可以训练一个 shallower 网络，然后在这个训练好的 shallower 网络上堆几层 identity mapping（恒等映射）的层，即输出等于输入的层，构建出一个 deeper 网络。这两个网络（shallower 和 deeper）得到的结果应该是一模一样的，因为堆上去的层都是 identity mapping。这样可以得出一个结论：理论上，在训练集上，Deeper 不应该比 shallower 差，即越深的网络不会比浅层的网络效果差。但为什么会出现图 1 这样的情况呢，随着层数的增多，训练集上的效果变差？这被称为网络退化问题（degradation problem），原因是随着网络越来越深，训练变得原来越难，网络的优化变得越来越难。理论上，越深的网络，效果应该更好；但实际上，由于训练难度，过深的网络会产生退化问题，效果反而不如相对较浅的网络。而残差网络就可以解决这个问题的，残差网络越深，训练集上的效果会越好。（测试集上的效果可能涉及过拟合问题。过拟合问题指的是测试集上的效果和训练集上的效果之间有差距。）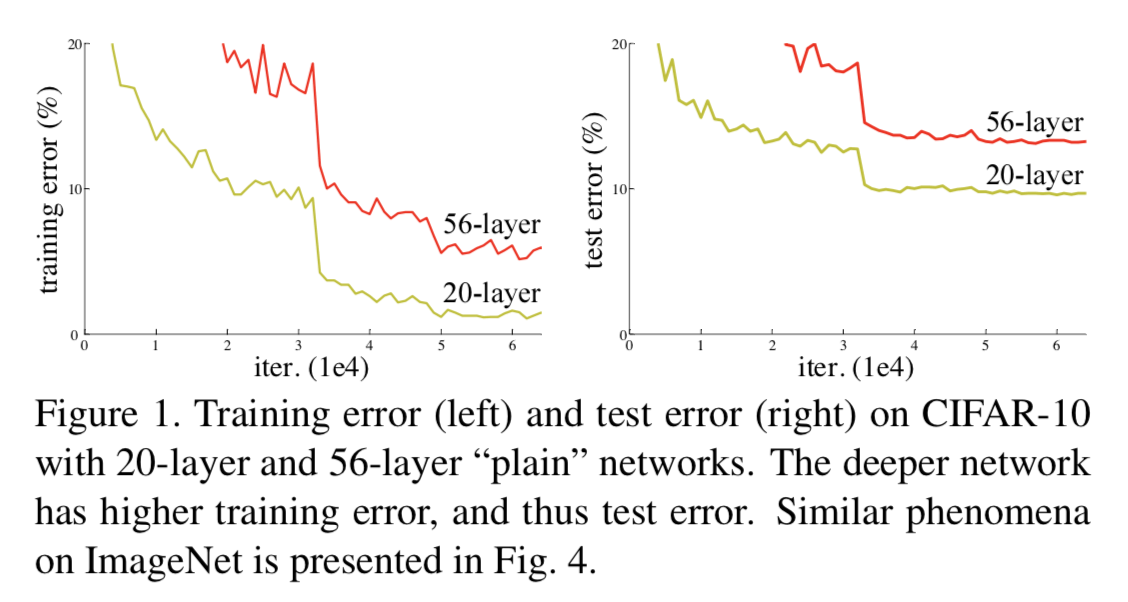

　残差网络通过加入 shortcut connections，变得更加容易被优化。包含一个 shortcut connection 的几层网络被称为一个残差块（residual block），如图 2 所示。（shortcut connection，即图 2 右侧从 x 到 ⨁ 的箭头）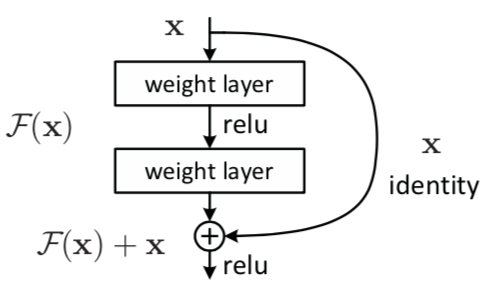
残差网络 - 图2
图 2 残差块

2 残差块（residual block）

　　如图 2 所示，xx 表示输入，F(x) 表示残差块在第二层激活函数之前的输出，即 F(x)=W2σ(W1x)，其中 W1和 W2表示第一层和第二层的权重，σσ表示 ReLU 激活函数。（这里省略了 bias。）最后残差块的输出是 σ(F(x)+x)。
　　当没有 shortcut connection（即图 2 右侧从 x 到 ⨁ 的箭头）时，残差块就是一个普通的 2 层网络。残差块中的网络可以是全连接层，也可以是卷积层。设第二层网络在激活函数之前的输出为 H(x)。如果在该 2 层网络中，最优的输出就是输入 x，那么对于没有 shortcut connection 的网络，就需要将其优化成 H(x)=x；对于有 shortcut connection 的网络，即残差块，如果最优输出是 x，则只需要将 F(x)=H(x)−x 优化为 0 即可。后者的优化会比前者简单。这也是残差这一叫法的由来。

3 残差网络举例

　　图 3 最右侧就是就是一个残差网络。34-layer 表示含可训练参数的层数为34层，池化层不含可训练参数。图 3 右侧所示的残差网络和中间部分的 plain network 唯一的区别就是 shortcut connections。这两个网络都是当 feature map 减半时，filter 的个数翻倍，这样保证了每一层的计算复杂度一致。
　　ResNet 因为使用 identity mapping，在 shortcut connections 上没有参数，所以图 3 中 plain network 和 residual network 的计算复杂度都是一样的，都是 3.6 billion FLOPs.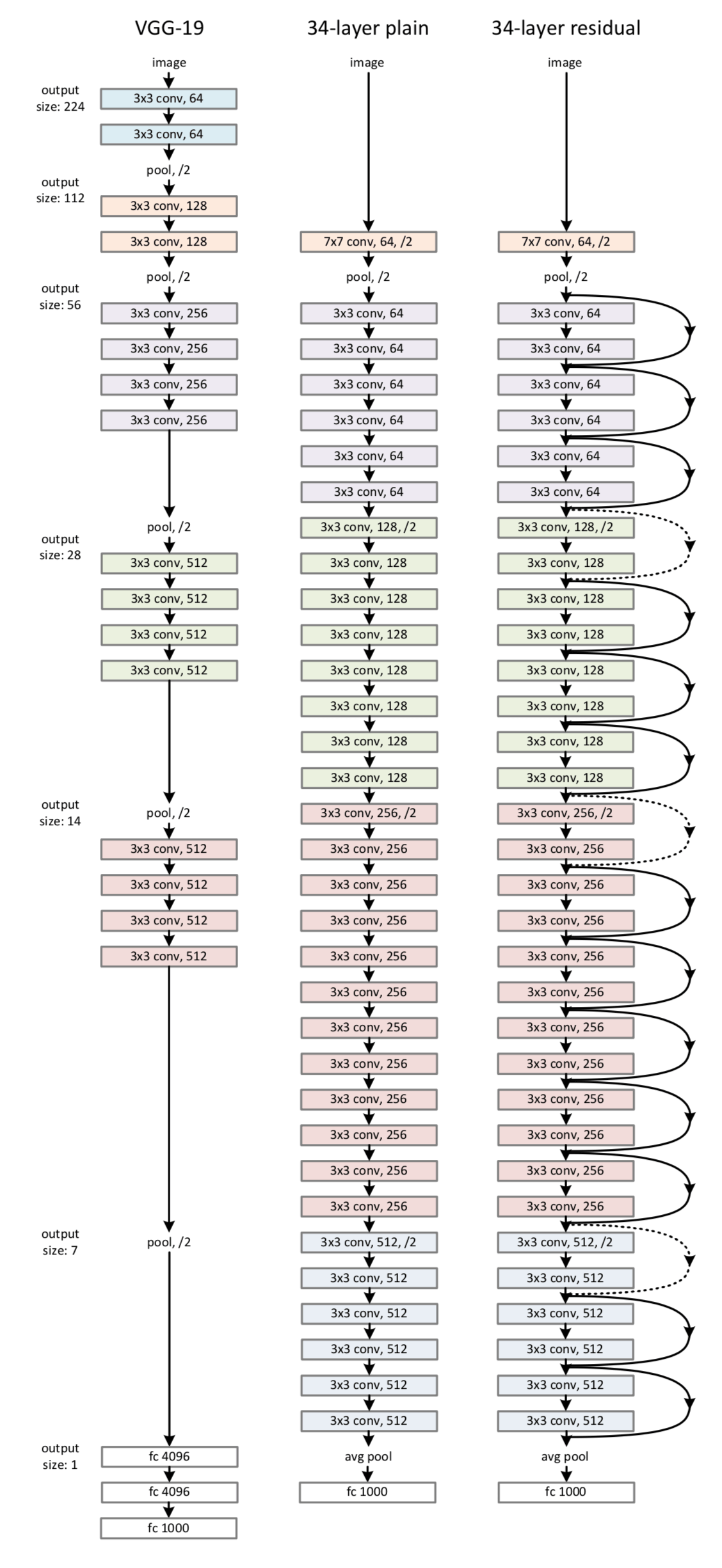
残差网络 - 图3
图 3 VGG-19、plain network、ResNet
　　残差网络可以不是卷积神经网络，用全连接层也可以。当然，残差网络在被提出的论文中是用来处理图像识别问题。

4 为什么残差网络会work？

　　我们给一个网络不论在中间还是末尾加上一个残差块，并给残差块中的 weights 加上 L2 regularization（weight decay），这样图 1 中 F(x)=0 是很容易的。这种情况下加上一个残差块和不加之前的效果会是一样，所以加上残差块不会使得效果变得差。如果残差块中的隐藏单元学到了一些有用信息，那么它可能比 identity mapping（即 F(x)=0）表现的更好。