蒙特卡罗算法

称为算法容易有误解，其实这是一种思想/方法，一种模拟方法，一种通过重复大量实验的模拟方法。基础理论是大数定律—在大量重复实验中，结果会呈现出明显的规律性，一般可总结为：“概率是频率的稳定值”。也就是说，通过做足够多的实验，其目标事件的出现频率可以近似概率，这就是蒙特卡罗算法的核心思想。

案例1

掷骰子，想知道点数为1的概率。可以通过重复投掷骰子100次，用点数1出现的次数除于100（也就是1的频率），将结果频率视为概率。如果想知道投3个骰子，同时为3个6的概率，一样可以通过重复实验100次、1000次来计算3个6出现的频率。

案例2

案例1很简单，但也很明了地展示了蒙特卡罗的思想和使用方式。蒙特卡罗还可以求积分，比如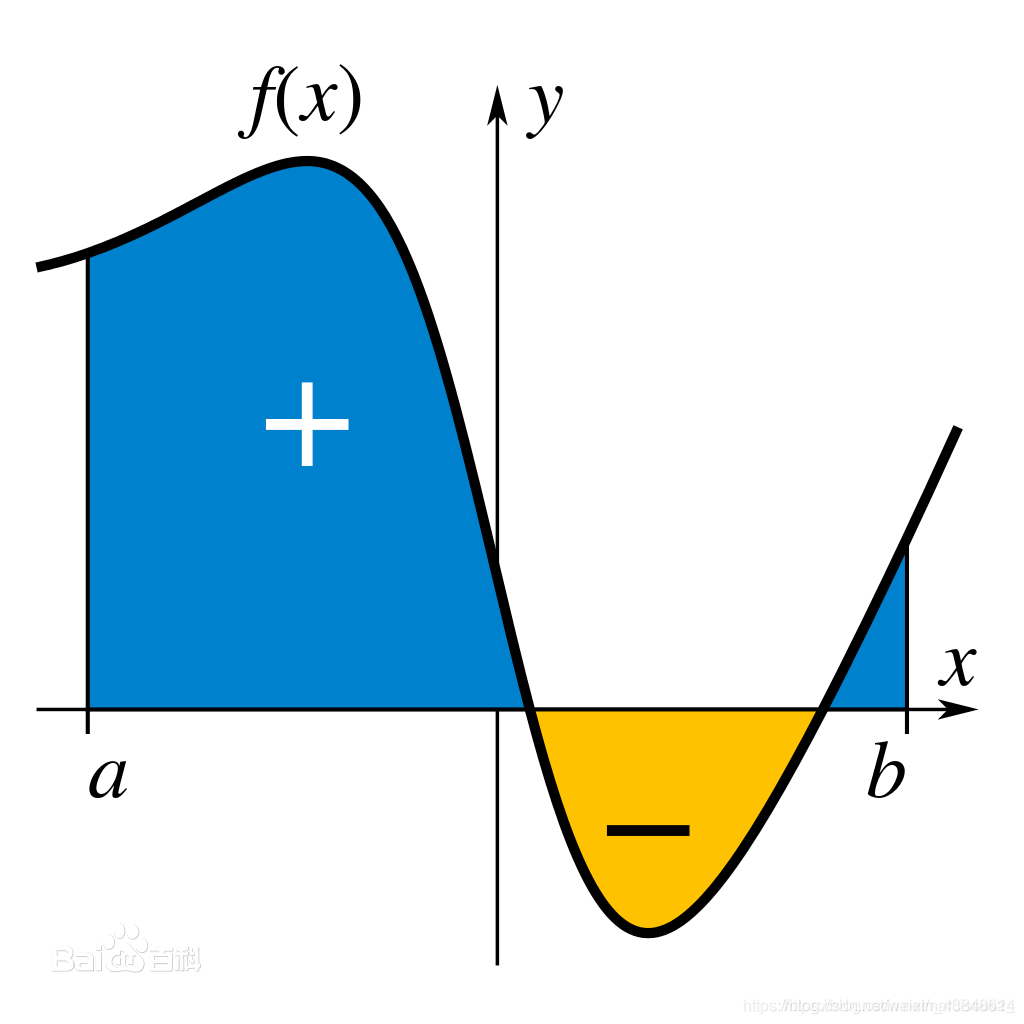


求解定积分相当于计算一个图形的面积。
按照牛顿和莱布尼兹的方法，我们是把区间划分成无限份，每份长为△t，高为f(a+z△t)，f(a+z△t)，这样来计算面积。

无论图形的形状如何，图形面积一定能被转化成一个以ab为底，y为高（y可以是负数）的长方形面积高，我们只
需要用蒙特卡洛算法求y即可。那么y怎么求，其实非常简单，我们只需要在a~b之间生成n个随机点，计算相应的f(x1),f(x2)…
然后计算被积函数平均值
于是整个函数的定积分理所当然为
具体方法：

1. 在区间[a,b]上利用计算机均匀产生n个随机数x1,x2…xn
2. 计算每一个随机数想对应的被积函数值f(x1),f(x2),f(xn)
3. 计算被积函数值的平均值。