交叉熵
分类问题中,预测结果是(或可以转化成)输入样本属于n个不同分类的对应概率。比如对于一个4分类问题,期望输出应该为 g0=[0,1,0,0] ,实际输出为 g1=[0.2,0.4,0.4,0] ,计算g1与g0之间的差异所使用的方法,就是损失函数,分类问题中常用损失函数是交叉熵。
交叉熵(cross entropy)描述的是两个概率分布之间的距离,距离越小表示这两个概率越相近,越大表示两个概率差异越大。对于两个概率分布 p 和 q ,使用 q 来表示 p 的交叉熵为: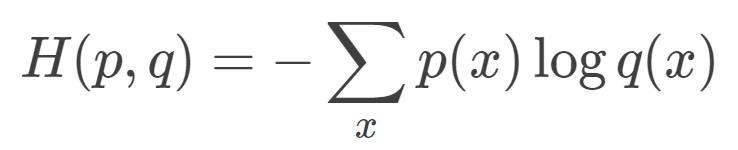
由公式可以看出来,p 与 q 之间的交叉熵 和 q 与 p 之间的交叉熵不是等价的。上式表示的物理意义是使用概率分布 q 来表示概率分布 p 的困难程序,q 是预测值,p 是期望值。
(题外 极大似然损失函数如下,像极了交叉熵,其实就是一回事)
softmax loss
softmax函数:
softmax loss是由softmax和交叉熵(cross-entropy loss)组合而成。
回到交叉熵的概念中,说到有4分类问题,实际输出和期望输出都是由概率组成的向量。问题是期望概率从哪里计算出来的?其实可以用softmax来解决。总的来说,就是先通过softmax得到概率向量,再用交叉熵作为损失函数。
神经网络的输出,也就是前向传播的输出可以通过Softmax回归变成概率分布,之后就可以使用交叉熵函数计算损失了。交叉熵一般会跟Softmax一起使用。
均方误差(MSE)家族
与分类任务对应的是回归问题,回归问题的任务是预测一个具体的数值,例如雨量预测、股价预测等。回归问题的网络输出一般只有一个节点,这个节点就是预测值。这种情况下就不方便使用交叉熵函数求损失函数了。回归问题中常用的损失函数式均方误差(MSE,mean squared error),定义如下:
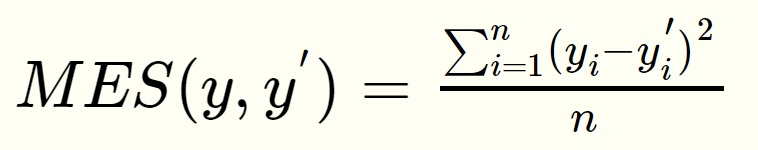
均方误差的含义是求一个batch中n个样本的n个输出与期望输出的差的平方的平均值。
对比
- 交叉熵没有使用预测值,而均方差使用了预测值。
- 交叉熵和softmax函数更适合分类问题,而均方差适合回归问题。
- 交叉熵适合用于二分类,softmax函数适合用于多分类。
- 如果将MSE用于分类问题,则必将经过某个变换(以sigmoid为例)。那么在损失函数初始化时,参数一般很小,容易造成梯度消失。参考https://www.yuque.com/shareit/yijiao/tvavle 第3.2节推导部分。
参考
- 交叉熵代价函数(损失函数)及其求导推导 (Logistic Regression)
https://blog.csdn.net/jasonzzj/article/details/52017438
- 交叉熵损失函数和均方误差损失函数

