参考：
https://www.jianshu.com/p/8b7324b0f307
https://zhuanlan.zhihu.com/p/59862986

二分类指标

在机器学习中，对于一个模型的性能评估是必不可少的。准确率(Accuracy)、查准率(Precision)、查全率(Recall)是常见的基本指标。
为了方便说明，假设有以下问题场景：

一个班有50人，在某场考试中有40人及格，10人不及格。 现在需要根据一些特征预测出所有及格的学生。

某一模型执行下来，给出了39人，其中37人确实及格了，剩下2人实际上不及格。

样本

要了解这些指标的含义，首先需要了解两种样本：

  • 正样本：即属于某一类（一般是所求的那一类）的样本。在本例中是及格的学生。
  • 负样本：即不属于这一类的样本。在本例中是不及格的学生。

    识别结果

    于是我们可以得到下面一张表：
正类 负类
被检索 True Positive False Positive
未检索 False Negative True Negative
  • TP：被检索到正样本，实际也是正样本（正确识别）
    在本例表现为：预测及格，实际也及格。
  • FP：被检索到正样本，实际是负样本（一类错误识别）
    在本例表现为：预测及格，实际不及格。
  • FN：未被检索到正样本，实际是正样本。（二类错误识别）
    在本例表现为：预测不及格，实际及格了。
  • TN：未被检索到正样本，实际也是负样本。（正确识别）
    在本例表现为：预测不及格，实际也不及格。

    指标计算

    有了上述知识，就可以计算各种指标了。

    Accuracy（准确率）

    分类正确的样本数 与 样本总数之比。即：(TP + TN) / ( ALL ).
    在本例中，正确分类了45人（及格37 + 不及格8），所以 Accuracy = 45 / 50 = 90%.

    Precision（精确率、查准率）

    被正确检索的样本数 与 被检索到样本总数之比。即：TP / (TP + FP).
    在本例中，正确检索到了37人，总共检索到39人，所以 Precision = 37 / 39 = 94.9%.

    Recall （召回率、查全率）

    被正确检索的样本数 与 应当被检索到的样本数之比。即：TP / (TP + FN).
    在本例中，正确检索到了37人，应当检索到40人，所以 Recall = 37 / 40 = 92.5%.

    为什么要不同的指标

    根据上边公式的不同，可以借此理解不同指标的意义。
    准确率是最常用的指标，可以总体上衡量一个预测的性能。但是某些情况下，我们也许会更偏向于其他两种情况。
    「宁愿漏掉，不可错杀」
    在识别垃圾邮件的场景中可能偏向这一种思路，因为我们不希望很多的正常邮件被误杀，这样会造成严重的困扰。
    因此，Precision 将是一个被侧重关心的指标。
    「宁愿错杀，不可漏掉」
    在金融风控领域大多偏向这种思路，我们希望系统能够筛选出所有有风险的行为或用户，然后交给人工鉴别，漏掉一个可能造成灾难性后果。
    因此，Recall 将是一个被侧重关心的指标。

多分类指标

本文以三分类模型举例。首先我们生成一组数据：

  1. import numpy as np
  2. y_true = np.array([-1]*30 + [0]*240 + [1]*30)
  3. y_pred = np.array([-1]*10 + [0]*10 + [1]*10 + 
  4.                   [-1]*40 + [0]*160 + [1]*40 + 
  5.                   [-1]*5 + [0]*5 + [1]*20)

数据分为-1、0、1三类，真实数据y_true中，一共有30个-1，240个0，30个1。然后我们生成真实数据y_true和预测数据y_pred的混淆矩阵，之后的演示中我们会用到混淆矩阵的数据：

  1. >>> confusion_matrix(y_true, y_pred)
  2. array([[ 10,  10,  10],
  3.        [ 40, 160,  40],
  4.        [  5,   5,  20]], dtype=int64)

由混淆矩阵我们可以计算出真正类数TP、假正类数FP、假负类数FN，如下：
二分类与多分类评价指标 - 图1
之后我们以precision_score的计算为例，accuracy_score、recall_score、f1_score等均可以此类推。
首先我们看一下sklearn包中计算precision_score的命令：

  1. sklearn.metrics.precision_score(y_true, y_pred, labels=None, pos_label=1, average=’binary’, 
  2.                                 sample_weight=None)

其中，average参数定义了该指标的计算方法，二分类时average参数默认是binary，多分类时，可选参数有micro、macro、weighted和samples。samples的用法我也不是很明确，所以本文只讲解micro、macro、weighted。

1 不加sample_weight

1.1 micro
micro算法是指把所有的类放在一起算，具体到precision，就是把所有类的TP加和，再除以所有类的TP和FN的加和。因此micro方法下的precision和recall都等于accuracy。
二分类与多分类评价指标 - 图2
使用sklearn计算的结果也是一样：

  1. >>> from sklearn.metrics import precision_score
  2. >>> precision_score(y_true, y_pred, average="micro")
  3. 0.6333333333333333

可以看到和手算是相同的。
1.2 macro
macro方法就是先分别求出每个类的precision再算术平均。
二分类与多分类评价指标 - 图3
用sklearn验证一下：

  1. >>> precision_score(y_true, y_pred, average="macro")
  2. 0.46060606060606063

1.3 weighted
前面提到的macro算法是取算术平均，weighted算法就是在macro算法的改良版，不再是取算术平均、乘以固定weight（也就是1/3）了，而是乘以该类在总样本数中的占比。计算一下每个类的占比：

  1. >>> w_neg1, w_0, w_pos1 = np.bincount(y_true+1) / len(y_true)
  2. >>> print(w_neg1, w_0, w_pos1)
  3. 0.1 0.8 0.1

然后手算一下weighted方法下的precision：
二分类与多分类评价指标 - 图4
用sklearn验证一下：

  1. >>> precision_score(y_true, y_pred, average="weighted")
  2. 0.7781818181818182

2 加入sample weight

当样本不均衡时，比如本文举出的样本，中间的0占80%，1和-1各占10%，每个类数量差距很大，我们可以选择加入sample_weight来调整我们的样本。
首先我们使用sklearn里的compute_sample_weight函数来计算sample_weight：

  1. sw = compute_sample_weight(class_weight='balanced',y=y_true)

sw是一个和ytrue的shape相同的数据，每一个数代表该样本所在的sample_weight。它的具体计算方法是总样本数/（类数每个类的个数），比如一个值为-1的样本，它的sample_weight就是300 / (3 30)。
使用sample_weight计算出的混淆矩阵如下：

  1. >>> cm =confusion_matrix(y_true, y_pred, sample_weight=sw)
  2. >>> cm
  3. array([[33.33333333, 33.33333333, 33.33333333],
  4.        [16.66666667, 66.66666667, 16.66666667],
  5.        [16.66666667, 16.66666667, 66.66666667]])

由该混淆矩阵可以得到TP、FN、FP: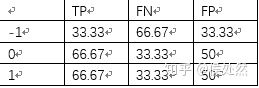
二分类与多分类评价指标 - 图5
三种precision的计算方法和第一节中计算的一样，就不多介绍了。使用sklearn的函数时，把sw作为函数的sample_weight参数输入即可。
本文介绍了一些sklearn应用时的细节，希望对读到这里的你有所帮助~